Вопрос 4. Комплексно-значные функции действ. Переменной. Кривые на комплекс. Пл. Функции комплекс. Переменного. Геометрич. Интерпритация.

Определение. Комплексно-значной функцией действительной переменной называется функция z=z(t), областью определения которой является некоторое подмножество пространства , а значениями – комплексные числа:

z(t)=x(t)+iy(t), где x(t)=Re(t), y(t)=Im(t).

Для функции z(t) справедливы след. утверждения и формулы:

1. Для непрерывной функции z(t) в точке t₀, необходимо и достаточно, чтобы и в этой точке были непрерывны функции x(t) и y(t).

2. _z'(t)= x'(t)+iy'(t), dz= dx+idy

3. 

Пусть дана непрерывная комплексно-значная функция z=z(t), t[α,β]. (1)

В этом случае на комплексной плоскости задана непрерывная кривая z=z(t), t[α,β]

Параметрическое уравнение кривой на комплексной плоскости:

Кривая (1) является упорядоченным множеством точек комплексной плоскости, ориентированным в направлении возрастания параметра t. Направление движения точки z вдоль кривой в направлении возрастания параметра t называется положительным.

Точка а=z(α) – начало, а b=z(β) – конец кривой.

Кривая (1), у которой начальная и конечная точка совпадают, называется замкнутой.

Кривая называется гладкой, если каждой точке она имеет касательную, непрерывно меняющую свое положение от точки к точке. Это означает, что функция z=z(t) непрерывно дифференцируема на [α,β] и на [α,β].

Кривая называется кусочно-гладкой, если z(t) непрерывна, и кривую можно разбить на конечное число гладких кривых. Кусочно-гладкая кривая спрямляема и её длина равна .

Определение. Функцией комплексной переменной называется отображение f некоторого подмножества D комплексной плоскости во множество .

f: D → .

При этом множество D называется областью определения функции f. Обозначается w=f(z).

w – образ точки z при отображении f, z – прообраз точки w при отображении f.

Пусть . Образом множества E при отображении f является .

Тогда f(D) называется множеством значений функции f. Для функции комплексной переменной вводят понятие инъективности, сюрьективности и биективности отображения, как и для функции действительной переменной.

Геометрическая интерпретация функции комплексного переменного.

Пусть w=f(z) задана на D. E - множество её значений. То есть каждой точке z=x+iy D ставится в соответствие точка w=f(z)=u+iv. Удобнее рассматривать две комплексные плоскости и , а функцию w=f(z) - как отображение из в . Часто считают, что плоскости и – одна и та же плоскость , тогда f задаёт отображение из в себя.

Пусть L D – некоторая кривая в плоскости . Eё образом при отображении f является некоторое множество точек К, которое может и не быть кривой. Пусть кривая в задана параметрически:

Т ак как отображение f задается равенствами: то образ кривой L имеет параметрические уравнения:

Образом области может и не быть область.

Вопрос 5. Определение предела функции. Необходим. И достаточное условие. Непрерывность функций. Примеры.

Пусть f(z) – однозначная функция, определённая на некотором множестве E и z₀ – предельная точка этого множества.

Определение 1 (по Коши). Комплексное число A называется пределом функции f(z) в точке z₀, если выполнено . Обозначается .

Определение 2 (по Гейне). Комплексное число A называется пределом функции f(z) в точке z₀, если выполнено .

Определение 3 (в терминах окрестностей). Комплексное число A называется пределом функции f(z) в точке z₀, если 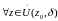выполнено .

Теорема. Для того, чтобы функция имела в точке z₀=x₀+iy₀ предел , необходимо и достаточно, чтобы .

Доказательство.

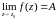1) Необходимость. Пусть . По определению

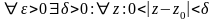выполнено .

.

Следовательно, и .

Значит, для выбранного и . Это означает что .

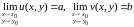2) Достаточность. Пусть .По определению:

выполнено ,

выполнено .

Пусть .

. Следовательно, .

Пусть w=f(z) определена в .

Определение 1. Функция называется непрерывной в точке z₀, если

.

Последнее условие равносильно: .

Обозначим . Тогда получим эквивалентное определение.

Определение 2. Функция f(z) называется непрерывной в точке z₀, если , то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Определение 3. Функция f(z) называется непрерывной в области D, если она непрерывна в каждой точке области D.

Теорема. Функция 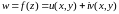непрерывна в точке z₀=x₀+iy₀ тогда и только тогда, когда u(x,y) и v(x,y) непрерывны в точке (x₀,y₀).

Свойства непрерывных функций:

1) Если функции f(z) и g(z) непрерывны в точке z₀, то функции fg, fg, также непрерывны в точке z₀.

2) Если функция f(z) непрерывна в точке z₀, то |f(z)| непрерывна в точке z₀.

3) Если функция t=g(z) непрерывна в точке z₀, а функция w=f(t) непрерывна в точке t₀=g(z₀), то сложная функция w=f((g(z)) непрерывна в точке z₀.

4) Если функция f непрерывна на ограниченной и замкнутой области D, то она на этой области ограничена: .

5) Если функция непрерывна на замкнутой ограниченной области D, то её модуль |f| имеет на D наибольшее и наименьшее значение.

Примеры.

 1) а) f(z)=z непрерывна в любой точке z₀ , так как .

б) f(z)=a, непрерывна на .

2) непрерывна на .

3) непрерывна на , кроме точек, в которых Q_m(z)=0.

4) так как u,v непрерывны на , то по теореме f(z) непрерывна на .

5) 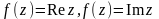непрерывны на . Пусть . Так как f(z)=z непрерывна, то в . Следовательно, непрерывна в z₀.

6) . .
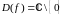