
- •Вопрос 1. Комплексные числа и действия над ними. Алгебраич. Форма записи числа. Геометрич. Интерпретация компл. Числа. Модуль и аргумент.
- •Вопрос 2. Модуль и аргумент комплексного числа. Тригоном. И показательная форма записи комплексного числа. Действия с компл. Числами, записан…
- •Вопрос 3. Определение предела послед. Комплексных чисел и его геом.Смысл. Необх. И достат. Условие. Критерий Коши. Бесконечно удаленная точка.
- •Вопрос 4. Комплексно-значные функции действ. Переменной. Кривые на комплекс. Пл. Функции комплекс. Переменного. Геометрич. Интерпритация.
- •Геометрическая интерпретация функции комплексного переменного.
- •Вопрос 5. Определение предела функции. Необходим. И достаточное условие. Непрерывность функций. Примеры.
- •Вопрос 6. Понятие производной функции комплекс. Переменной. Определение функции диф. В точке и области. Теорема о непрерывности. Правила диф.
- •Вопрос 7. Определение функции диф. В точке и области. Необходимые и достаточные условия дифференцируемости функции.
- •Вопрос 8. Геометрический смысл аргумента и модуля производной. Понятие конфорного отображения.
- •Вопрос 9. Общие степенная и показательная функции. Логарифм.
- •Вопрос 10. Понятие интеграла от функции комплекс. Переменного и свойства.
- •Вопрос 11. Понятие числового ряда в комплексной области. Сходимость. Критерий Коши.
- •Вопрос 12. Последовательности и ряды функций комплексного переменного
- •Вопрос 13. Изолированные особые точки и их классификация.
- •Вопрос 14. Бесконечно удаленная изолированная особая точка
Вопрос 9. Общие степенная и показательная функции. Логарифм.
Введем понятие степени с произвольным показателем.
Пусть
а0
–произвольное число. Если
 ,
то, как известно
,
то, как известно
an=|a|n(cos(nArga)+isin(nArga)),
если

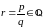 ,
где
,
где
 и
и

 - несократимая дробь, то
- несократимая дробь, то
 ,
,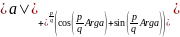
где
 -
единственное действительное положительное
значение степени числа |a|.
-
единственное действительное положительное
значение степени числа |a|.
Пусть

- иррациональное число. Зафиксируем
=Arga
и рассмотрим последовательность {rn}
рациональных чисел, сходящуюся к
тогда
- иррациональное число. Зафиксируем
=Arga
и рассмотрим последовательность {rn}
рациональных чисел, сходящуюся к
тогда
 .
.
Это
значение примем за одно из значений
степени a.
Чтобы получить остальные значения,
будем придавать Arga
различные значения. Так как два различных
значения  Arga
отличаются на
Arga
отличаются на 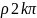 2k,
а это число не может быть целым кратным
2
(так как
2k,
а это число не может быть целым кратным
2
(так как  - иррациональное число), то все значения
a,
соответствующие различным значениям
Arga
различны.
- иррациональное число), то все значения
a,
соответствующие различным значениям
Arga
различны.
Итак, если 
 ,
то
,
то
a= (cos(Arga)+isin(Arga)
(cos(Arga)+isin(Arga) ), (21)
), (21)
Причем,
если
 ,
то получаем одно значение, если
,
то получаем одно значение, если
 ,то q
значений, и если
- иррациональное число, то бесконечное
множество значений.
,то q
значений, и если
- иррациональное число, то бесконечное
множество значений.
Пусть

 .
Формулу (21) можно записать в виде:
.
Формулу (21) можно записать в виде:
a=eln|a|(cos(Arga)+isin(Arga))=exp(ln|a|+iArga)=
=exp((ln|a|+iArga))=exp(Lna).
Определение.
Пусть
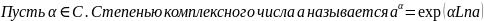 .
Степенью
комплексного числа а
называется
.
Степенью
комплексного числа а
называется
a= exp(Lna).
Замечание. Для степени с произвольным показателем, вообще говоря,
1)
 ,
,  2)
2)
 .
.
 ,
,

 .
.
С другой
стороны,
 .
Значит, в общем случае
.
.
Значит, в общем случае
.
Определение.
Степенной функцией комплексной
переменного
называется функция вида
f(z)=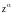 =exp(Lnz),
. (22)
=exp(Lnz),
. (22)
Она
определена вообще
 .
Степенная функция в общем случае (но не
всегда!) многозначна. Если
.
Степенная функция в общем случае (но не
всегда!) многозначна. Если
 ,
то –конечнозначна (
,
то –конечнозначна ( -значна),
если
-значна),
если ,
то- бесконечнозначна.
,
то- бесконечнозначна.
Каждому
значению независимой переменной z
соответствует счетное множество значений
степени z.
Если справа в (22) брать одну определенную
ветвь Lnz,то
будем получать
соответствующие
ветви степенной функции. Например,
 .
.
Отдельные
ветви, т.е. однозначные функции
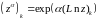 являются аналитическими функциями на
комплексной плоскости с разрезом вдоль
отрицательной действительной полуоси.
По правилу производной сложной функции:
являются аналитическими функциями на
комплексной плоскости с разрезом вдоль
отрицательной действительной полуоси.
По правилу производной сложной функции:
 .
.
Например, .
.
Определение.
Функция вида
 , (24)
, (24)
где
, ,
называется общей
показательной функцией.
,
называется общей
показательной функцией.
Эта
функция многозначна в силу многозначности
Lna.
Чтобы получить определенную однозначную
ветвь, надо фиксировать одно из значений
 .
.
Пусть ,тогда
,тогда ,
,


 .
.
При
 ,
т.е. когда берем главное значение Lne,
получим
,
т.е. когда берем главное значение Lne,
получим
 ,
т.е. это значение совпадает с изученной
нами функцией
,
т.е. это значение совпадает с изученной
нами функцией
 .
.
Зафиксируем
 функции
функции
 одно из значений логарифма:
одно из значений логарифма:
 .
Тогда мы получим однозначную ветвь
функции
.
Тогда мы получим однозначную ветвь
функции
 и можем рассмотреть обратную к ней
функцию. Получим
и можем рассмотреть обратную к ней
функцию. Получим
 .
.
Так
как
 ,
то w
можно рассматривать как логарифм z
по основанию a.
,
то w
можно рассматривать как логарифм z
по основанию a.
Определение.
Логарифмом
произвольного комплексного числа
 по некоторому основанию a
(
-комплексное
число) называется
по некоторому основанию a
(
-комплексное
число) называется
 ,
,
где в знаменателе стоит одно фиксированное значение Lna.
Вопрос 10. Понятие интеграла от функции комплекс. Переменного и свойства.
Пусть
на комплексной плоскости
задана кривая L,
которая является простой и гладкой,
т.е.
 ,
причем
,
причем
а) функции
x(t)
и y(t)
непрерывно дифференцируемы на [,]
и

 (гладкая кривая), б) различным значениям
параметра t
соответствуют различные точки кривой
L
(простая
кривая).
(гладкая кривая), б) различным значениям
параметра t
соответствуют различные точки кривой
L
(простая
кривая).
Точки
z()
и z()-
начало и конец кривой L.
Если z()=z(),
то кривая называется замкнутой.
 Пусть на кривой
Пусть на кривой
 (т.е.
в каждой ее точке) определена функция
комплексного переменного f(z).
Пусть T-
произвольное разбиение кривой L
точками
(т.е.
в каждой ее точке) определена функция
комплексного переменного f(z).
Пусть T-
произвольное разбиение кривой L
точками
 ,
взятыми в порядке возрастания параметра
t,
на частичные дуги
,
взятыми в порядке возрастания параметра
t,
на частичные дуги
 .
Обозначим через
.
Обозначим через
 длину дуги
.
На каждой частичной дуге
выберем произвольную точку
длину дуги
.
На каждой частичной дуге
выберем произвольную точку
 .
Обозначим
.
Обозначим
 ,
,
 ,
,
 .
.
Составим интегральную сумму для функции f(z) по кривой L,соответствующую данному разбиению T и выбору точек :
 . (1)
. (1)
Определение.
Если
существует конечный предел интегральной
суммы (1) при
 (или
при
(или
при
 ),
не зависящий ни от способа разбиения T
кривой L,
ни от выбора точек
,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
),
не зависящий ни от способа разбиения T
кривой L,
ни от выбора точек
,
то этот предел называется интегралом
от функции f(z)
по кривой L
и обозначается
 .
Таким образом,
.
Таким образом,
 .
.
В этом случае функция f(z) называется интегрируемой по кривой L.
Теорема
1 (достаточное
условие существования интеграла от
функции комплексного переменного).
Пусть L
– простая гладкая кривая на
,
f(z)=u(x;y)+iv(x;y)
непрерывна на L.
Тогда существует
 ,
причем справедливо равенство:
,
причем справедливо равенство: . (2)
. (2)
Доказательство.
Выберем произвольно разбиение T
кривой L
на дуги
,
на каждой
выберем произвольно точку
.
Составим интегральную сумму
.
Выделим в
 действительную и мнимые части:
действительную и мнимые части:
z=x+iy,
f(z)=u(x;y)+iv(x;y),
 ,
,
 ,
,
 ,
,
 ,
,
 .
Тогда
.
Тогда

 . (3)
. (3)
В правой
части (3) стоят интегральные суммы для
криволинейных интегралов II
типа двух действительных функций u(x;y)
и v(x;y).
Если
 и
и
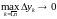 ,
то и
,
то и

 (или
).
(или
).
Т.к. L – гладкая кривая, а функции u(x;y) и v(x;y) непрерывны на L, то

 и
и  .
.
Тогда существует предел при левой части (3), т.е. существует .
Переходя в (3) к пределу при , получим (2).
Свойства:
1
Линейность интеграла
 .
.
2
Аддитивность. Если
 (
где
(
где
 и
и
 не имеют общих точек за исключением
начала
и конца
),
то
не имеют общих точек за исключением
начала
и конца
),
то .
.
3 ,
где
,
где
 -
кривая L,
пройденная в противоположном направлении.
-
кривая L,
пройденная в противоположном направлении.
4
 ,
где s
–длина дуги, отсчитываемая от начала
L
до произвольной точки в выбранном
направлении.
,
где s
–длина дуги, отсчитываемая от начала
L
до произвольной точки в выбранном
направлении.
 .
Т.к.
.
Т.к.
 -длина хорды, то
-длина хорды, то
 - где
- где
 длина дуги
длина дуги
 ,
следовательно,
,
следовательно,
 .
Переходя к пределу при
.
Переходя к пределу при
 ,
получим
,
получим
 .
.
5
Если
 ,
то
,
то
 ,
где L
–длина кривой L.
,
где L
–длина кривой L.
5
 .
.
