Вопрос 6. Понятие производной функции комплекс. Переменной. Определение функции диф. В точке и области. Теорема о непрерывности. Правила диф.

Пусть функция w=f(z) определена в окрестности точки z₀ U(z₀). Придадим точке z₀ произвольное приращение так, чтобы z₀+∆zU(z₀). Тогда функция получит приращение: .

Составим отношение (функция от ∆z).

Определение 1. Если существует конечный , то он называется производной функции f в точке z₀, и обозначается .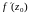

Определение 2. Функция f(z) называется дифференцируемой в точке z₀, если ее приращение в этой точке можно представить в виде , где (не зависит от ∆z), .

Определение 2 (эквивалентно определению 2). Функция f(z) называется дифференцируемой в точке z₀, если в этой точке она имеет конечную производную.

Определение. Функция f(z) называется дифференцируемой в области G, если она дифференцируема в каждой точке z этой области.

Теорема 2 (необходимое условие дифференцируемости). Если функция f(z) дифференцируема в точке z₀, то она непрерывна в этой точке.

Доказательство. Так как f(z) дифференцируема в точке z₀, то по определению

, .

Тогда . Значит, по определению, f(z) дифференцируема в точке z₀.

Основные правила дифференцирования:

1. .

2. .

3. .

4. , g(z)0.

5. Производная сложной функции. Пусть w=f(t), где t=g(z). Тогда

.

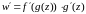6. Производная обратной функции.

w=f(z), D(f) – область определения, E(f) – множество значений. непрерывна на E. Пусть w₀=f(z₀). Если дифференцируема в точке z₀ и , то дифференцируема в точке w₀=f(z₀) и .

7. =с, . 8. =z, . 9. , n .

Вопрос 7. Определение функции диф. В точке и области. Необходимые и достаточные условия дифференцируемости функции.

Определение 2. Функция f(z) называется дифференцируемой в точке z₀, если ее приращение в этой точке можно представить в виде , где (не зависит от ∆z), .

Определение 2 (эквивалентно определению 2). Функция f(z) называется дифференцируемой в точке z₀, если в этой точке она имеет конечную производную.

Определение. Функция f(z) называется дифференцируемой в области G, если она дифференцируема в каждой точке z этой области.

Теорема 3. Пусть функция определена в некоторой области G. Для того, чтобы функция f(z) была дифференцируемой в точке z области G необходимо и достаточно, чтобы

1. функции u(x;y) и v(x;y) были дифференцируемы в точке z как функции двух действительных переменных;

2. в точке z выполнялись равенства

и . (1)

При выполнении всех условий теоремы производная может быть представлена в одном из следующих видов:

. (2)

Равенства (1) называются условиями Коши-Римана (или Даламбера-Эйлера).

Доказательство.

1) Необходимость.

Пусть функция f(z) дифференцируема в точке z области G. Тогда по теореме 1 ее приращение может быть представлено в виде

, где .

- комплексная функция от z. Следовательно, , где . - комплексное число, значит, , a,b . Тогда

f(z)=u+iv=(a+ib)(x+iy)+(₁+i₂)(x+iy)=ax-by+i(ay+bx)+

+₁x-₂y+i(₁y+₂x)=(ax-by+₁x-₂y)+i(ay+bx+₁y+₂x).

Отсюда

u=ax-by+₁x-₂y,

v=bx+ay+₂x+₁y, где . (3)

Из (3) следует, что

1) функции u(x;y) и v(x;y) дифференцируемы в точке (x;y),

2) их частные производные в точке (x;y):

, ,

, .

Отсюда , , т.е. удовлетворяют условиям Коши-Римана.

Тогда для производной получаем:

.

2) Достаточность.

Пусть в точке z области G выполнены условия 1) и 2) теоремы. Придадим точке z=(x;y) приращение z=x+iy0. По условию

где . (4)

Приращение функции , соответствующее приращению , имеет вид: . Разделим на :

. Используя условия Коши-Римана, перейдём к частным производным по x:

. (5)

Т.к. , , и , то и (огр.БМФ).

Следовательно, переходя в (5) к , получим:

, т.е. f(z) дифференцируема в точке z.

Определение. Производной второго порядка от функции комплексного переменного называется производная от ее производной первого порядка:

, и т.д, .