
- •Применение теории игр в экономических задачах
- •Оглавление
- •1. Теоретические сведения
- •1.1. Основные понятия теории матричных игр
- •1.2. Смешанные стратегии и теорема фон Неймана-Нэша
- •Теорема фон Неймана-Нэша
- •1.3. Метод решения игры
- •Приведение матричной игры к задаче линейного программирования
- •2. Пример выполнения задания
- •3. Задание к лабораторной работе
- •Согласно заданному варианту в таблице приводятся элементы платежной матрицы и вероятностей использования стратегий 2-ым игроком.
2. Пример выполнения задания
Игра задана платежной матрицей А.
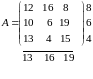
Для
определения нижней цены игры
выберем в каждой строке платежной
матрицы минимальный элемент, затем из
полученного столбца выберем максимальный
элемент. Получим нижнюю цену игры:
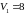 .
.
Для
определения верхней цены игры
выберем в каждом столбце матрицы
максимальный элемент, тогда минимальный
элемент из полученной строки и есть
верхняя цена игры:
 .
.
Из
условия
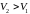 следует, что игру необходимо проводить
в смешанных стратегиях.
следует, что игру необходимо проводить
в смешанных стратегиях.
1) Пусть заданы вероятности использования противником своих стратегий: у = (0,2; 0,5; 0,3).
Необходимо определить оптимальное поведение и максимальный выигрыш первого игрока. Для этого рассчитаем его выигрыш в случае применения им всех своих стратегий по формуле:
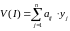

При заданных условиях первый игрок должен применить свою третью стратегию, в этом случае он получит максимальный выигрыш равный 15,1.
2) Необходимо решить задачу 2x2, вычеркнув из заданной платежной матрицы столбец и строку таким образом, чтобы полученные в новой матрице и не совпадали. Например, вычеркнем из исходной матрицы третью строку и первый столбец, получим новую матрицу:
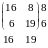
у
которой
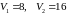 .
.
Решение задачи свелось к решению системы:
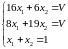
Используем формулу (1.3.2):
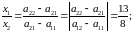
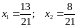 .
.
Вычислим выигрыш первого игрока:
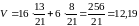 ;
;
 .
.
Отсюда
вывод: первому игроку следует использовать
свои стратегии с частотой
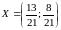 ,
при этом его гарантированный выигрыш
будет равен 12,19 ед., что существенно выше
чем
.
,
при этом его гарантированный выигрыш
будет равен 12,19 ед., что существенно выше
чем
.
Для второго игрока решение сведется к системе:
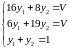
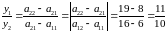 ;
; 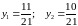 .
.
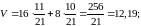
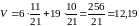 .
.
Используя
смешанные стратегии с частотой
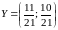 ,
второй игрок может понизить свой
гарантированный протгрыш с 16 ед. до
12,19 ед.
,
второй игрок может понизить свой
гарантированный протгрыш с 16 ед. до
12,19 ед.
3)
Игра
 .
.
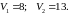
Любая
игра
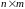 сводится к задаче линейного
программирования. Для первого игрока
ограничения и целевая функция выглядят
следующим образом:
сводится к задаче линейного
программирования. Для первого игрока
ограничения и целевая функция выглядят
следующим образом:
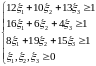
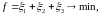
где
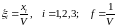
Для решения полученной задачи используем симплекс-метод, реализованный в программе LINPROG. При этом получим оптимальное решение:
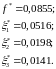
Перейдем к исходным переменным:
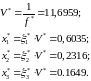
Из
полученных результатов следует, что
максимальный гарантированный выигрыш
первого игрока составит 11,6959 при условии,
что он будет применять свою первую
стратегию с частотой
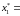 0,6035,
вторую − с частотой
0,6035,
вторую − с частотой
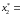 0,2316
и третью − с частотой
0,2316
и третью − с частотой
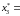 0,1649.
0,1649.
Для второго игрока задача линейного программирования является двойственной к предыдущей и имеет вид:
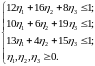
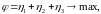
где
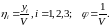
Для решения использовалась программа LINPROG. Полученное оптимальное решение имеет вид:
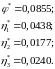
Перейдем к исходным переменным:

Из
полученных результатов следует, что
минимальный гарантированный проигрыш
второго игрока составит 11,6959 в случае
если он будет
использовать
свою первую стратегию с частотой
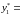 0,5123,
вторую − с частотой
0,5123,
вторую − с частотой
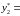 0,2070,
третью − с частотой
0,2070,
третью − с частотой
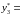 0,0240.
0,0240.
3. Задание к лабораторной работе
Игра задана платежной матрицей А. Получить решение задачи в случае, если:
1. Заданы стратегии противника;
Из платежной матрицы вычеркнуты строка и столбец таким образом, чтобы нижняя и верхняя цены игры не совпали (игра 2 х 2);
3. Решить задачу полностью (игра 3 х 3) с использованием персонального компьютера (программа LINPROG).
