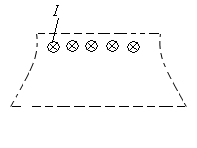
5. Циркуляция вектора магнитной индукции. Закон полного тока.

По определению циркуляция вектора равна интегралу . Вычислим этот интеграл в случае прямого тока.

	Пусть замкнутый контур лежит в плоскости, перпендикулярной к току (рис. 23.8). В каждой точке контура вектор направлен по касательной к окружности, проходящей через точку А. Расстояние от тока до т. А обозначим . Скалярное произведение , где – проекция на направление вектора . В силу малости угла , можно найти как длину дуги .
Рис. 23.8

Магнитная индукция, создаваемая бесконечным прямолинейным током . Тогда .

Интегрируя по контуру , получим:

.

Обобщая полученный результат на случай произвольного количества токов в силу принципа суперпозиции ( )

.

В результате получаем закон полного тока:

Циркуляция вектора магнитной индукции вдоль произвольного замкнутого контура прямо пропорциональна алгебраической сумме токов, охватываемых этим контуром.

Например, применительно к полю бесконечного прямого тока:

(очень просто!)

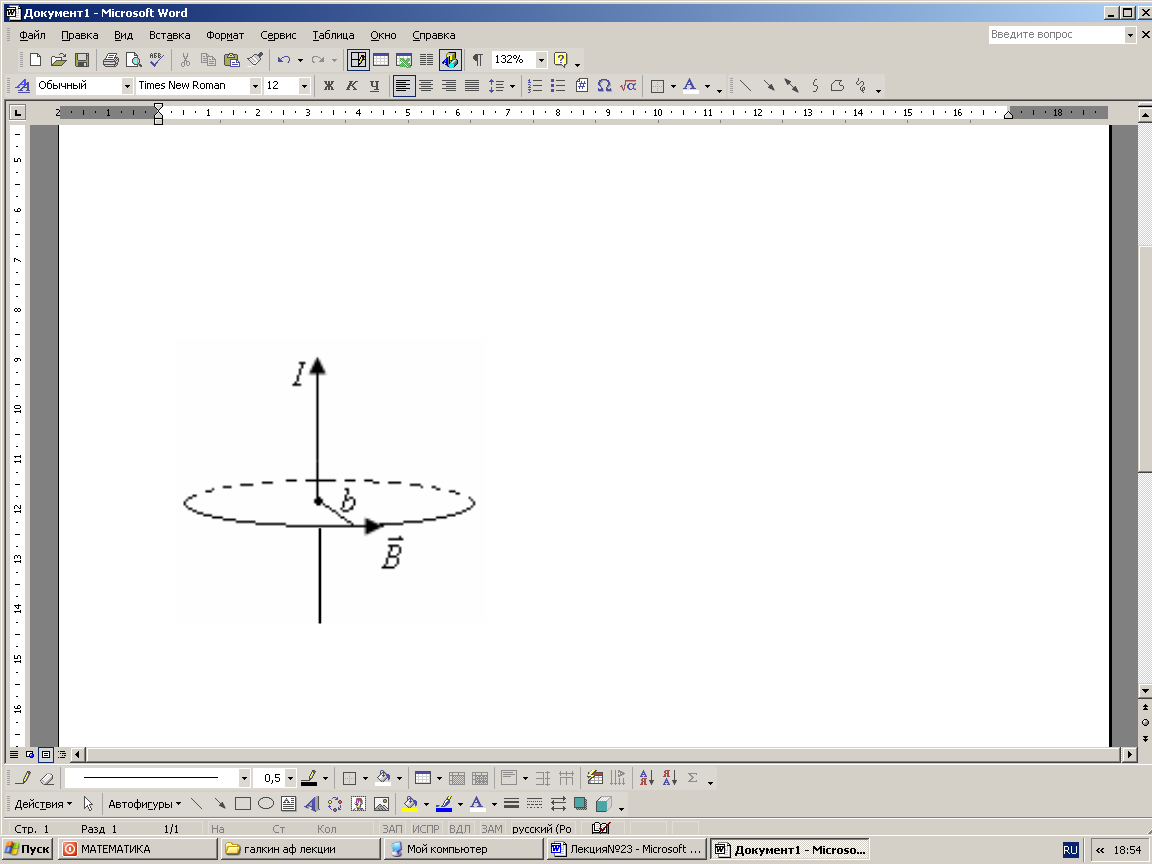
Магнитное поле длинного соленоида и тороида

а) Соленоид (от греч. «солен» - трубка) – провод, навитый в виде спирали на круглый цилиндрический каркас. Длинным можно считать соленоид, у которого длина в 5-6 раз больше диаметра. Пренебрегая концевыми эффектами, поле внутри соленоида можно считать однородным. Пусть число витков , длина соленоида , ток (рис. 23.9).

	Выберем контур таким образом, чтобы одна сторона была вдоль оси (1-2) соленоида, другая параллельна ей достаточно далеко (3-4), где , и две стороны (2-3) и (4-1) перпендикулярны силовым линиям (из соображений симметрии ясно, что они направлены вдоль оси). Циркуляция: В соответствии с законом полного тока , , итак, поле
Рис. 23.9
	соленоида: где – число витков на единицу длины.
Рис. 23.10

б

Рис. 23.11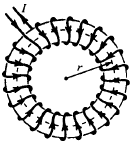

) Тороид представляет собой провод, навитый как каркас, имеющий форму тора (рис. 23.11). Из соображений симметрии нетрудно понять, что силовые линии вектора должны быть окружностями, центры которых расположены на оси тороида. Ясно, что в качестве контура следует взять одну из таких окружностей (показана пунктиром). Если контур расположен внутри тороида, он охватывает ток , где – число витков в тороидальной катушке; - ток в проводе. Пусть радиус контура , тогда по теореме о циркуляции , откуда следует, что внутри тороида .

Будем считать много больше толщины тороида, тогда – длина тороида , поле тороида:

где , как и для соленоида, число витков на единицу длины.

6. Магнитное взаимодействие токов.

П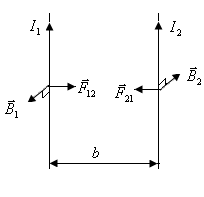 рименим закон Ампера для вычисления взаимодействия двух находящихся в вакууме параллельных бесконечно длинных прямых токов (рис. 23.12). Если расстояние между токами , то каждый элемент тока будет находиться в магнитном поле тока , индукция которого равна

У

Рис. 23.12

гол между элементами тока и вектором прямой. Следовательно, на элемент тока действует сила Ампера: , подставим , .

Разделим обе части на :

То есть сила, действующая на элемент тока со стороны другого тока пропорциональна произведению сил токов и обратно пропорциональна расстоянию между токами.

На основании полученного соотношения устанавливается единица силы тока в системе СИ – ампер – сила неизменяющегося тока, который, проходя по двум прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенными на расстоянии 1 м один от другого, вызвал бы между этими проводниками силу взаимодействия, равную на каждый метр длины.

Заметим, что при одинаковом направлении токи притягивают друг друга, а при различном – отталкивают.