Лекция 2.

Продолжение темы

«Выборочные характеристики и точечные оценки»

Покажем, что выборочная дисперсия является смещенной оценкой дисперсии ². Преобразуем формулу выборочной дисперсии к эквивалентному виду:

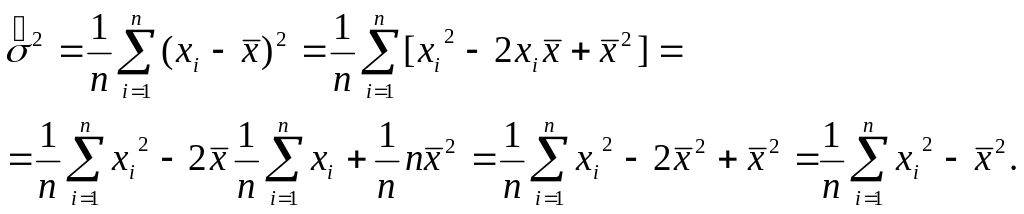
Поскольку выборочная дисперсия, как и теоретическая, не изменяется от прибавления к значениям случайной величины фиксированного числа, то ее можно записать в виде:

Действительно, доказательство утверждения вытекает из следующей цепочки равенств:

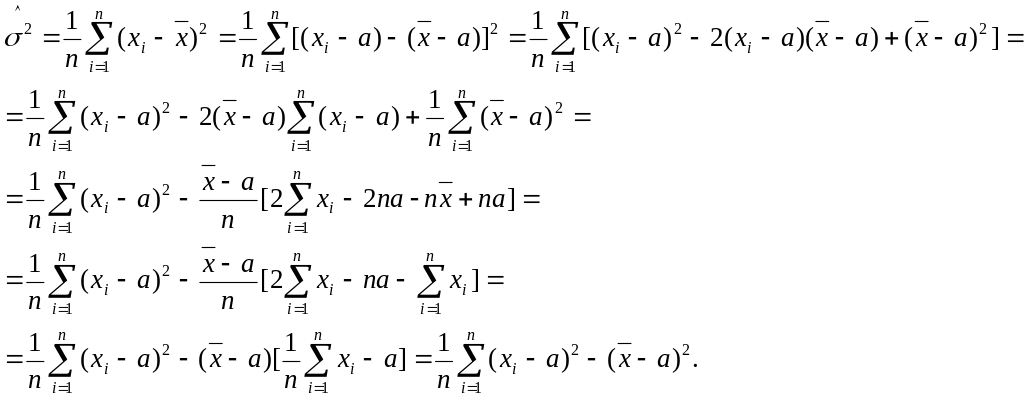
Вычислим математическое ожидание выборочной дисперсии:

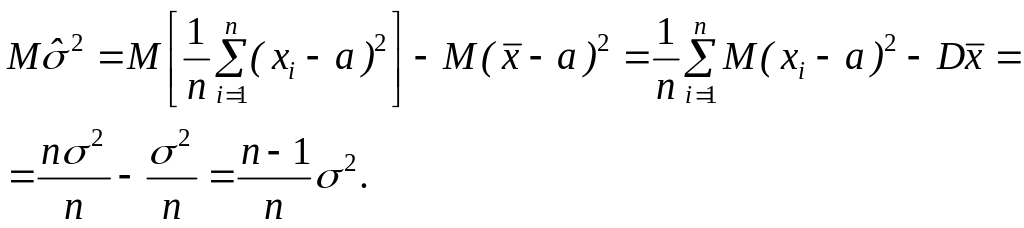
Отсюда следует, что является смещенной оценкой дисперсии.

Несмещенной оценкой дисперсии будет , так как

Поэтому оценку (при получении которой сумма делится на n) называют смещенной или неисправленной выборочной дисперсией, а оценку s² (при получении которой сумма делится на n–1) называют несмещенной или исправленной выборочной дисперсией. Выборочным средним квадратическим отклонением (исправленным или неисправленным) называют положительный корень из соответствующей выборочной дисперсии. Эта оценка теоретического среднего квадратического отклонения , к сожалению, в обоих случаях является смещенной.

Обычный закон больших чисел не применим к центрированным величинам, так как после центрирования они становятся зависимыми. Доказать, что выборочная дисперсия сходится по вероятности к теоретической дисперсии, если последняя существует, можно с помощью теоремы Слуцкого.

Теорема Слуцкого. Пусть функция f(x,y) непрерывна в точке (а,b) и случайные последовательности X_n и Y_n сходятся по вероятности соответственно к числам a и b. Тогда f(X_n,Y_n) сходится по вероятности к f(a,b).

Доказательство. Если f(x,y) непрерывна в точке (a,b), то для любого  >0 существует  такое, что при x-a< и y-b< выполняется неравенство f(x,y)–f(a,b)<. Тогда, если f(x,y)–f(a,b)≥, то справедливо одно из неравенств или x–a≥ или y–b≥. Рассмотрим событие :

{,f(x_n,y_n)–f(a,b)}{,x_n–a≥}{,y_n–b≥}.

Поскольку события {,x_n–a≥} и {,y_n–b≥} несовместны, то в силу теоремы сложения несовместных событий получим

P(f(x_n,y_n)–f(a,b))P(x_n–a)+P(y_n–b),

причем

P(x_n–a)0 и P(y_n–b)0 при n.

Следовательно, вся сумма стремится к нулю, т.е.

P(f(x_n,y_n)–f(a,b))=0 или f(x_n,y_n) f(a,b).

Для доказательства сходимости по вероятности выборочной дисперсии к теоретической достаточно рассмотреть функцию f(x,y)=x–y², положив

X_n= a²+², Y_n= a (при n),

и применить теорему Слуцкого.

Подобным образом доказывается сходимость по вероятности всех выборочных центральных моментов _k, если существуют _k=M(–a)^k, а также некоторых их модификаций – асимметрии, эксцесса и т.п.

Случайная последовательность ₁, ₂, ..., _n,… называется асимптотически нормальной, если существуют числовые последовательности А₁,А₂,... и В₁,В₂,... (В_i>0 для всех i) такие, что

при n.

Здесь Ф(х) – функция стандартного нормального распределения. Числа А_i и B_i называются параметрами асимптотически нормально распределенной случайной величины _i. Условие, что последовательность ₁, ₂, ..., _n,… асимптотически нормальна, записывается в виде _i N(A_i,B_i).

Используя введенный термин, центральную предельную теорему можно сформулировать следующим образом: пусть ₁,₂,...,_n,… – независимые одинаково распределенные случайные величины с конечными моментами первого и второго порядков: M_i=а; D_i=². Тогда если S_n =₁+₂+...+_n, то S_n N(na,n²), n.

Теорема 7.3.2. Если распределение генеральной совокупности имеет конечные математическое ожидание a и дисперсию ², то при n основные выборочные характеристики являются асимптотически нормальными:

1. ;

2. ;

3. .

Другими словами, при больших объемах выборки все основные выборочные характеристики можно считать практически нормально распределенными.

Теорема Доказать, что если – несмещенная оценка параметра  и при n, то оценка состоятельная.

Решение. Поскольку , то из неравенства Чебышева для любого  > 0 получаем:

при n. Следовательно, .