Лекция 3

Методы построения оценок. Метод моментов.

Метод моментов, предложенный английским статистиком Карлом Пирсоном в 1894 г., заключается в приравнивании определенного числа выборочных моментов к соответствующим теоретическим, которые являются функциями неизвестных параметров ₁, ₂, …, _k. Рассматривая количество моментов, равное числу k неизвестных параметров, подлежащих определению, и решая полученные уравнения относительно этих параметров, получаем искомые оценки. Иначе говоря, оценки параметров ₁,₂,…,_k являются решениями систем уравнений

или для некоторых .

Метод моментов содержит неопределенность, поскольку можно получить уравнения для неизвестных параметров, используя как начальные, так и центральные моменты, а также некоторые их модификации типа асимметрии или эксцесса.

Пример. Функция

задает плотность распределения Рэлея.

Найдем оценку параметра , приравнивая начальные выборочные и теоретические моменты. Первый теоретический начальный момент имеет вид:

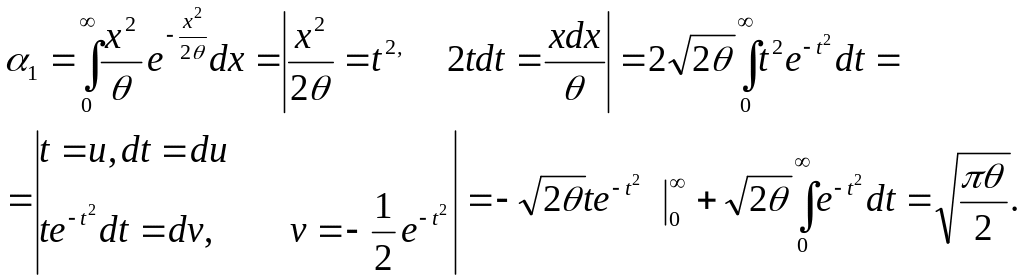
Приравнивая, первому эмпирическому моменту , получаем первую оценку параметра . Приравнивая вторые начальные моменты, можем получить другую оценку: , а из уравнения, которое возникает при использовании второго центрального момента (дисперсии), третью оценку: .

Рекомендуется для нахождения оценки одного параметра брать первый момент, для двух – первые два момента и т.п. Однако этот подход годится не всегда. Он не проходит, например, если некоторые моменты равны нулю или не зависят от нужных параметров.

Оценки, полученные методом моментов, часто оказываются смещенными. К достоинствам метода моментов следует отнести его простую вычислительную реализацию, а также то, что оценки являются функциями от выборочных моментов.

В силу теоремы Слуцкого любая непрерывная функция от выборочных моментов сходится по вероятности к постоянной, получаемой подстановкой в эту функцию теоретических моментов, если они существуют и если получаемая таким образом постоянная конечна. Для определенности рассмотрим функцию Н(₁,₂) от двух моментов (начальных или центральных), хотя результат можно обобщить на любое конечное число аргументов.

Теорема 7.6.1 (теорема Крамера). Пусть в некоторой окрестности точки (₁,₂) функция Н(₁,₂) непрерывна и имеет непрерывные частные производные первого и второго порядка. Обозначим

Н₁= , Н₂= и Н₀=Н(₁,₂) .

Тогда случайная величина асимптотически нормальна при n со следующими параметрами:

.

На практике часто возникает необходимость оценить не сами параметры распределения (которые представляют собой некие абстракции), а определенные экономически значимые показатели, зависящие от этих параметров функционально: G=g(₁,₂,…,_k). Самый простой (хотя и не самый точный) способ такого оценивания – подставить полученные оценки в соответствующую функцию: .

Задача Случайная величина  (число появлений события А в m независимых испытаниях) подчинена биномиальному закону распределения с неизвестным параметром р. Ниже приведено эмпирическое распределение числа появлений события в 10 опытах по 5 испытаний в каждом (в первой строке указано число х_i появлений события А в одном опыте; во второй строке указана частота n_i – количество опытов, в которых наблюдалось столько появлений события А):

xi	0	1	2	3	4
ni	5	2	1	1	1

Найти методом моментов точечную оценку параметра р биномиального распределения. Оценить вероятность p₀=P(=0).

Решение. Математическое ожидание биномиального распределения известно: M=mp. Приравняв математическое ожидание к выборочному среднему, получим уравнение: , откуда . Для рассматриваемого примера имеем:

;

= 1,1/5 = 0,22; (10,22)⁵0,29.

Задача Предполагается, что выполнение некоторой работы занимает случайное время с распределением Симпсона на отрезке [a, b]. Хронометраж 20 испытаний дал среднее время работы 30 мин и исправленную выборочную дисперсию 24 мин². Оценить параметры a и b методом моментов. Оценить, за какое время работа будет выполняться с вероятностью 98%.

Решение. Для распределения Симпcона (плотность которого имеет вид равнобедренного треугольника с основанием на заданном отрезке) имеем

; .

Параметры распределения можно выразить через математическое ожидание и дисперсию:

;

.

Подставляя вместо теоретических моментов выборочные, получаем оценки

; ,

откуда =18 (мин), =42 (мин).

Функция распределения Симпсона имеет вид:

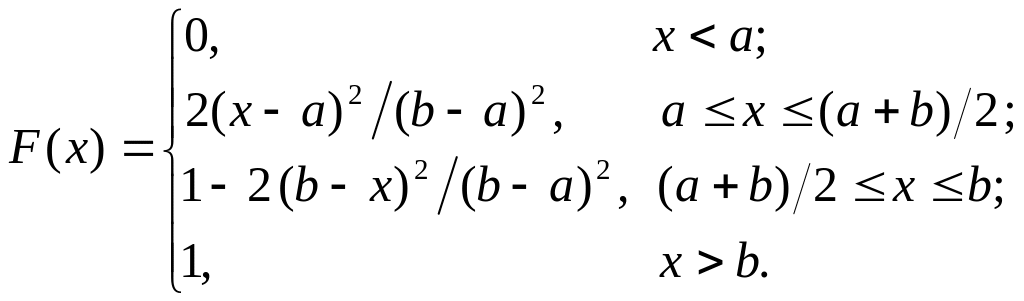
Решая уравнение F(x)=0,98, находим искомое время T=b0,1(ba).

Подставляя полученные оценки в формулу вместо теоретических параметров, получаем =420,1(4218)=39,6 (мин).

Иногда оценки, получаемые с помощью метода моментов, принимаются в качестве первого приближения, по которому можно построить другими методами оценки более высокой эффективности.