Б. Непрерывные распределения

Задача Методом максимального правдоподобия найти оценки параметров а и  нормального распределения, плотность которого: .

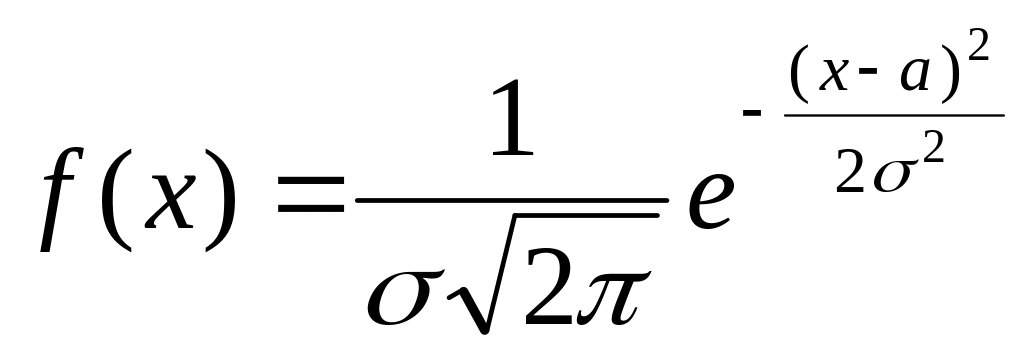Решение. Выпишем функцию правдоподобия:

.

Логарифмическая функция правдоподобия имеет вид:

.

Найдем точку максимума, решив систему из двух уравнений, получающихся путем приравнивания первых двух частных производных по неизвестным параметрам к нулю:

 

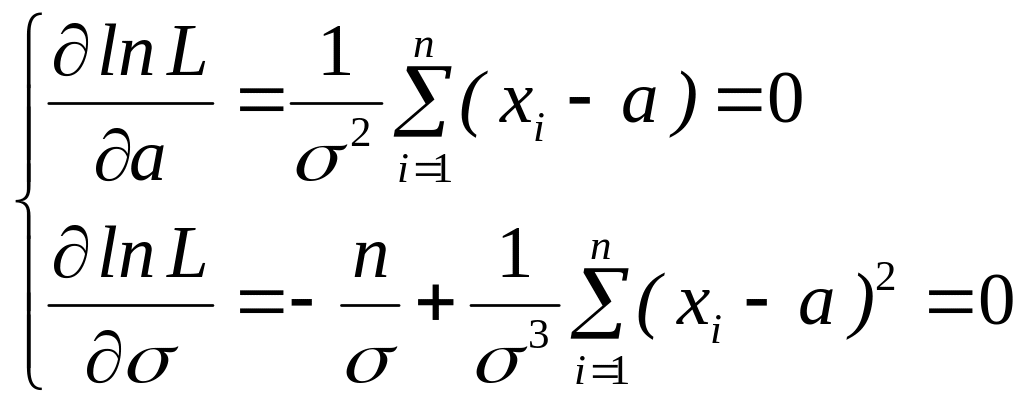
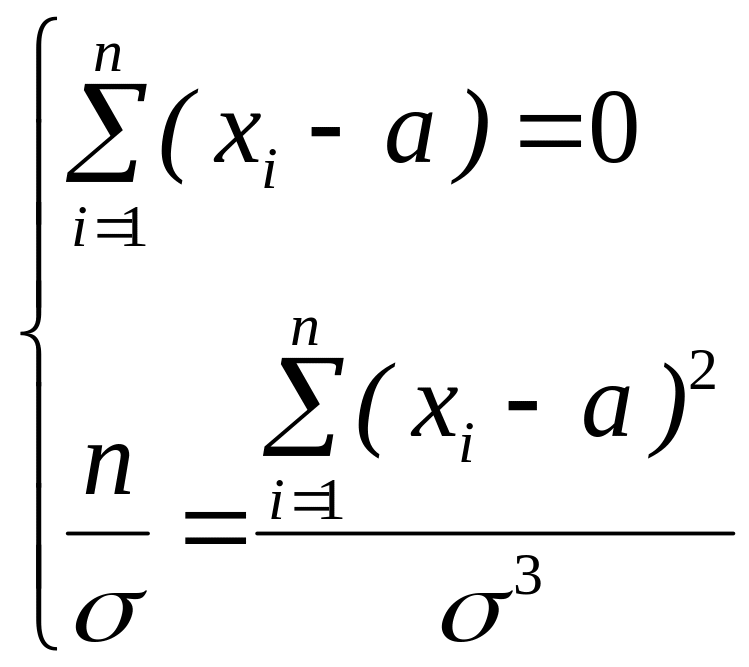
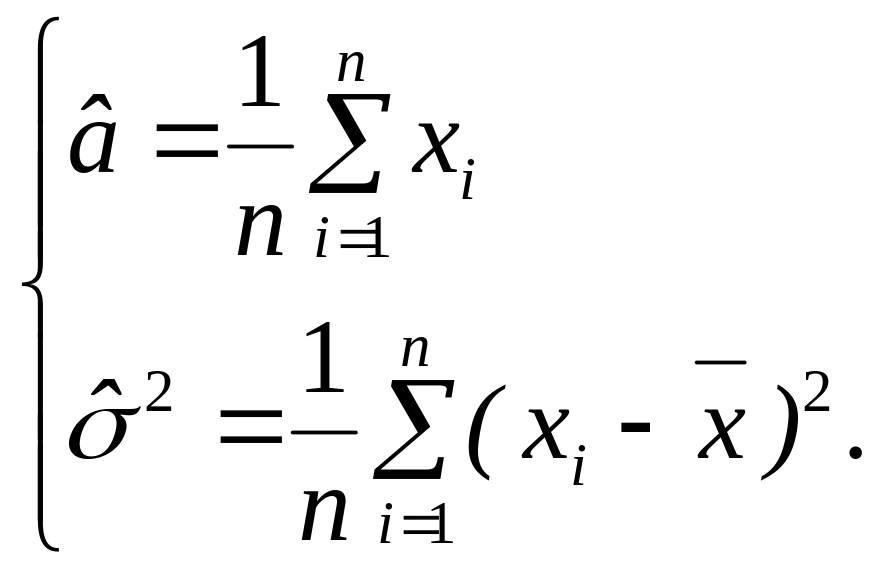
Проверим, является ли точка точкой максимума функции правдоподобия:

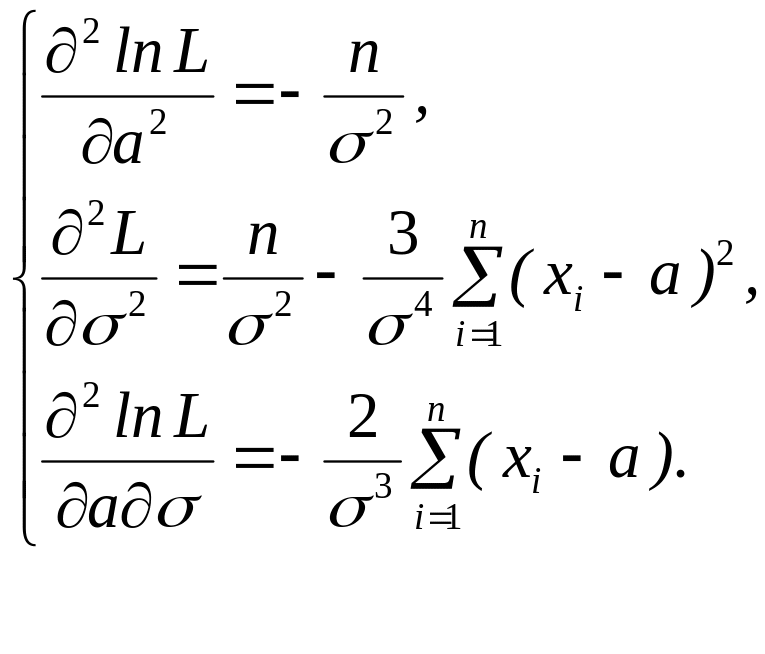
Как известно из математического анализа, чтобы функция

f(х₁, х₂,…, х_n) достигала максимума в некоторой точке, достаточно, чтобы матрица второго дифференциала функции d²f в этой точке была отрицательно определена. По критерию Сильвестра для этого необходимо и достаточно, чтобы ее главные миноры чередовались по знаку, а именно ₁ < 0, ₂ > 0. Рассмотрим матрицу производных:

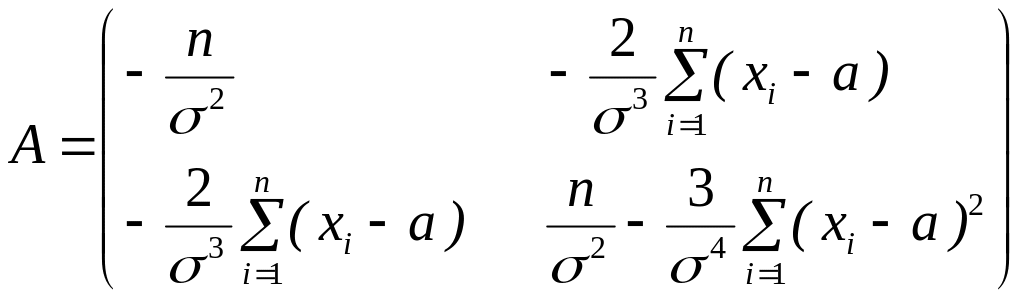
Отсюда

₁ = < 0;

₂ = .

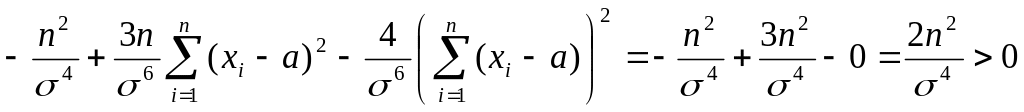Следовательно, точка – действительно точка максимума, и полученные оценки являются оценками максимального правдоподобия.

Задача Найти оценку максимального правдоподобия для параметра сдвига  распределения Коши, заданного плотностью , по выборке из двух наблюдений, если: а) x₁ = 1, x₂=1; б) x₁ = 2, x₂=2.

Решение. Функция правдоподобия для двух наблюдений имеет вид

.

Введем функцию . Тогда задача максимизации функции правдоподобия эквивалентна задаче минимизации R(θ).

а) Если x₁=1, x₂=1, то . Функция R достигает минимума в точке =0, так что это и есть оценка максимального правдоподобия.

б) Если x₁ = 2, x₂=2, то . В этом случае производная имеет три нуля: в точках =0 и = . При этом точка =0 оказывается точкой максимума функции R. Точкам = соответствует минимум функции R, причем в обеих этих точках величина R одинакова. Таким образом, оба значения являются в данном случае оценками максимального правдоподобия.

Замечание. Ни метод моментов, ни метод максимального правдоподобия не могут дать хороших оценок для параметра сдвига распределения Коши. Тем не менее, существует простая оценка для него – выборочная медиана: =x_med, поскольку F()=1/2.

В. Нерегулярные случаи

Задача Найти методом максимального правдоподобия оценки параметров а и b равномерного закона распределения:

Решение. Заметим, что в данном случае не выполняются условия регулярности, поскольку плотность не только недифференцируема, но даже разрывна (как функция от a и b).

Выпишем функцию правдоподобия для равномерного распределения:

L(x₁, x₂,…, x_n) = , если все x_i [a, b],

L(x₁, x₂,…, x_n) = 0, иначе.

Если брать частные производные и приравнивать их к нулю, то легко убедиться, что полученные уравнения правдоподобия не имеют решений. В данном случае нужно действовать другим способом.

Условие, что все наблюдения принадлежат отрезку [a, b], можно выразить через неравенства для крайних членов вариационного ряда: ax_min, bx_max. При фиксированном значении a функция правдоподобия убывает по b при bx_max и, следовательно, принимает максимальное значение при b=x_max. При фиксированном значении b функция правдоподобия возрастает по a при ax_min и, следовательно, принимает максимальное значение при a=x_min.Таким образом, оценками максимального правдоподобия будут крайние члены вариационного ряда : = x_min и = x_max.

Задача Построить оценку методом максимального правдоподобия параметра сдвига  для распределения Лапласа с плотностью .

Решение. Функция правдоподобия имеет вид

.

Логарифмируя, получаем:

.

Заметим, что эта функция недифференцируема во всех точках х₁, х₂,…, х_n, а в остальных точках производная имеет вид:

Отсюда следует, что функция правдоподобия возрастает, если слева от значения  находится меньше членов вариационного ряда, чем справа, и убывает в противном случае. Следовательно, максимума она достигает посередине вариационного ряда. Если n=2k+1, то это происходит в точке x_(k). Если n=2k, то функция постоянна на интервале (x_(k), x_(k+1)), где принимает наибольшее значение, и в качестве оценки можно взять середину этого интервала. Таким образом, оценкой максимального правдоподобия оказывается выборочная медиана: =x_med.