13. Мера сходства и ее свойства.

Для решения задач распознавания вводится мера сходства, которая опирается на систему аксиом. В зависимости от решаемой задачи и функции, определяющей меру сходства, аксиоматика, на которую она опирается, может быть различной. Рассмотрим следующую систему аксиом.

В качестве первой аксиомы примем аксиому о том, что меры сходства объектов x и y из множества А по совокупности свойств изменяются в конечном интервале. Эту аксиому, называемую аксиомой ограничения, запишем следующим образом: 0≤μ≤1.

В качестве второй аксиомы примем аксиому о том, что меры сходства объектов x и y из множества А по совокупности свойств должны быть равны. Эту аксиому, называемую аксиомой симметрии, запишем так:. .

В качестве третьей примем аксиому о том, что мера сходства объектов x и y из множества А по совокупности свойств достигает максимума, когда объекты x и y неразличимы по совокупности свойств. Эту аксиому, называемую аксиомой максимального сходства, запишем следующим образом: .

В качестве четвертой примем аксиому о том, что мера сходства объектов x и y из множества А по совокупности свойств в общем случае обращается в нуль лишь на некоторых заранее фиксированных парах противоположных граничных объектов x_гр, y_гр. Данная аксиома, называемая аксиомой минимального сходства, записывается следующим образом: .

В качестве пятой аксиомы примем аксиому о том, что мера сходства объектов x и y из множества А по совокупности свойств ψ должна быть функцией от мер сходства по отдельным свойствам ψ_i, входящим в совокупность свойств ψ.

14. Метрика и ее свойства.

В математике раньше появилось понятие метрики.

Метрика — это любая функция p(x, y), определяющая расстояние между двумя объектами и удовлетворяющая условиям:

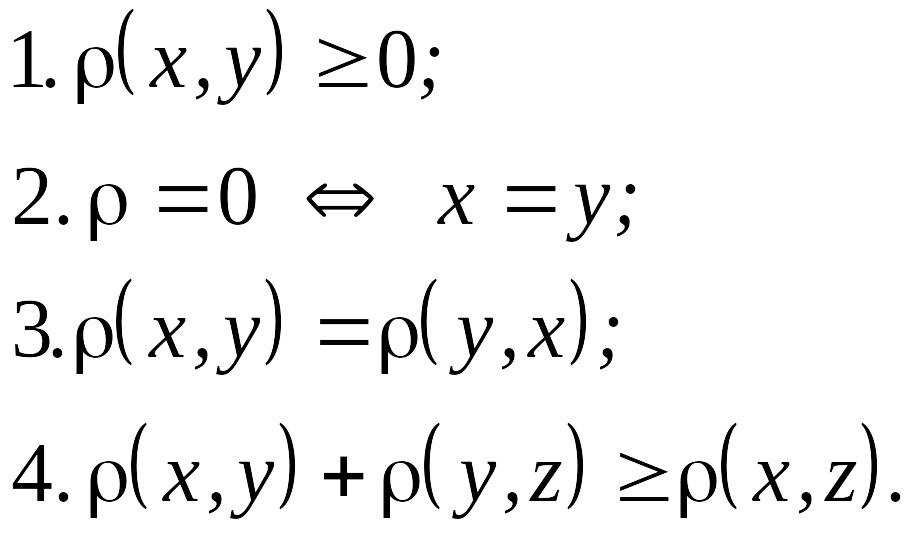
Чаще всего на практике мера сходства строится на основании метрики, т.к. метрика является хорошо изученным математическим объектом.

16. Алгоритм «Гол n»

Назначение — решение задач распознавания в ситуациях, когда в МО представлены объекты K образов (K=2,3..).

Постановка задачи. В исходных данных, представленных в виде ТОС, присутствуют представители всех образов. Для каждого объекта указана его принадлежность к образу. В процессе распознавания определяется принадлежность объектов экзамена к одному из образов. Распознавание проводится в двух режимах: с отказом и без отказа.

Метод решения задачи.

Пусть совокупность экспериментально изученных объектов a₁,a₂,..,a_n со свойствами представлена в виде таблицы «объекты-свойства»:

, ,

где m — число свойств, n — число объектов и для каждого объекта указана принадлежность к образу.

Свойства могут быть измерены в различных шкалах (арифметическая, логическая 1-го рода, логическая 2-го рода).

Данный алгоритм решается как алгоритм Голотип-1, но с некоторыми отличиями, которые состоят в следующем.

1. Постоянная для разбиения на компоненты связности выбирается так, чтобы связанными между собой оказались те объекты, для которых мера сходства не меньше средних мер сходства между объектами внутри образов и максимальных мер сходства между образами. По этой причине в одну компоненту связности всегда попадают только объекты, относящиеся к одному образу, т.е. компоненты связности однородны.

2. Радиусы компонент связности выбираются таким образом, чтобы в компонентах связности связи, описанные шарами, не попали объекты других образов.

Процедура экзамена проводится с отказом и без отказа. В режиме распознавания с отказом объект экзамена X относится к той компоненте связности, в которую он попадает ( , где q — номер компоненты, — ее голотип, R_q — ее радиус, и соответственно к тому образу, к которому относится голотип ). В режиме распознавания без отказа объект X относится к той компоненте связности, к голотипу которой он оказывается ближе всего в смысле величины меры сходства, и соответственно к тому образу, к которому относится этот голотип.

Условия применимости.

ТОС должна быть без пропусков; свойства — арифметические, логические 1-го и 2-го рода.