Тема 2.4. Обыкновенные дифференциальные уравнения.

1. Обыкновенные дифференциальные уравнения.

ДУ – ур-е, содержащее неизвестную ф-цию, независимую переменную и ее производные различных порядков.

Если искомая ф-ция зависит от одной переменной, то ДУ – обыкновенное ДУ (ОДУ).

Если искомая ф-ция содержит 2 и > независ переменных, то ДУ назывур-е в частных производных.

В общем виде ОДУ можно записать F(x,y,y’,у`` … , y⁽ⁿ⁾)=0 (1), где F – ф-я от (n+2) переменных, х – неизвестная переменная, y=y(x) –искомая ф-я

Порядок старшей производной, входящей в ур-е назывпорядком ур-я.

Если ур-е можно представить в виде y⁽ⁿ⁾ =f(x,y,y’,…,y^(n-1)), где f- ф-я, определенная в некоторой обл. DϲRⁿ⁺¹,то говорят, что это ур-е разрешено относительно старшей производной, и его называют диф.ур-ем в нормальной форме.

2. Понятие решения.

ф-ция у=у(х) назрешением ДУ если, будучи подставленным в соответствующур-е вместе со всеми своими произв-ми, она обр-т его в верное рав-во. Задача нах-я решения ДУ наз задачей интегрирования ДУ.

Общим решением ДУn-го порядка назыв ф-ция вида y=(x,c₁,c₂,…,c_n), которая зависит от переменной х и nпроизвольных постоянных

_{Частичным} реш ДУназреш, получ из общего при некот конкретных числовых значениях постоянных c₁,c₂,…,c_n

3. Дифференци­альные уравнения первого порядка.

_{Как следует из определения обыкновенным дифференциальным уравнением первого порядка называется уравнение F(x, y, y ') = 0,где x - независимая переменная, y(x) - неизвестная функция.}

_{В форме, разрешённой относительно производной, уравнение первого порядка записывается так: y '= f(x, y)}

Уравнения первого порядка часто записывают в дифференциальной форме:

M(x, y)dx + N(x, y)dy = 0.

Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .

Задача Коши.

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

Уравнения с разделяющимися пере­менными.называется дифференциальное уравнение вида f(x)dx + g(y)dy = 0с непрерывными функциями f(х) и g(y).

Равенство где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0 .

Уравнением с разделяющимися переменными называется дифференциальное уравнение вида f1(x)g1 (y)dx + f2(x) g2(y)dy =0 .

Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0 .

Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными

Общий интеграл этого уравнения имеет вид

Линейные дифференциальные уравнения первого порядка.

ДУ вида A(x)y’+B(X)y+C=0, где A(x)≠0, или после деления на A(x), приведённое к виду y’+p(x)y=q(x), называется линейным ДУ первого порядка. Если q(x)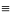 0, то уравнение называется линейным однородным, иначе – линейным неоднородным.

Линейное однородное уравнение – это уравнение с разделяющимися переменными, его общее решение выражается формулой .

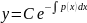Для решения линейного неоднородного уравнения можно применять метод вариации произвольной постоянной, тогда общее решение неоднородного уравнения получается в виде .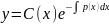

y(x) = u(x) v(x): из этого выражения находим u(x), и y(x) = u(x) v(x).

Линейное неоднородное уравнение может быть сведено к решению двух уравнений с разделяющимися переменными при помощи подстановки(метод Бернулли)y(x) = u(x) v(x) двух неизвестных дифференцируемых ф-и й u(x) и v(x).Тогда , и уравнение приводится к виду , или .

Найдем функцию v(x) как некоторое ненулевое частное реш-е однородного ур-я . затем находим u(x) из уравнения _{. после нахождения} v(x) определяем u(x) как реш-е ур-я . тогда . отсюда реш-е линейного неоднородного ур-я сводится к реш-ю двух ур-ей с раздедяющимися переменными и имеет вид .

Линейные диф ур-я второго порядка с пост коэф­фициентами. имеет вид

Линейным однородным уравнением второго порядка называется уравнение . Уравнение будем называть линейным неоднородным уравнением.

Общее реш-е линейного однородногодиф.ур-я имеет вид: y=C₁y₁(x)+C₂y₂(x)

Для неоднородного линейного ур-я общее реш-е имеет вид:y= C₁y₁(x)+C₂y₂(x)+µ(x)

Еслиp(x)≡p, q(x)≡q – постоянные, то линейное ур-е называется уравнением с постоянными коэффициентамии записывают его так: . Для нахождения y₁(x), y₂(x)этого ур-я при f(x)=0 составляет квадратноеур-е λ²λ+pλ+q=0, кот-е назыв. характеристическим.

Возможны 3 вар-та:

D>0 корни ур-яλ_1, λ₂различные. Общее реш-е однородногоур-я y=C₁e^λ₁^x+C₂e^λ₂^x

D=0 корниλ₁₌λ₂₌λодинаковые. тогдереш-е y=e^λx( C₁+C₂x)

D<0 корни ур-я λ_1,2=α^+/-iβ(i=корень из -1). реш-е y=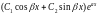

Понятие о комплексных числах.

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a = c и b = d.

Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d).

Произведением двух комплексных чисел a + ib и c + id называется комплексное число ac – bd + i(ad + bc).

Геометрическое представление комплексного числа

Комплексная экспонента.

Комплексная экспонента — математическая функция, задаваемая соотношением , где z есть комплексное число.

Однородные и неоднородные уравнения.

ДУ вида A(x)y’+B(X)y+C=0, где A(x)≠0, или после деления на A(x), приведённое к виду y’+p(x)y=q(x), называется линейным ДУ первого порядка. Если q(x) 0, то уравнение называется линейным однородным, иначе – линейным неоднородным.

Линейным однородным уравнением второго порядка называется уравнение . Уравнение будем называть линейным неоднородным уравнением.

Линейные диф ур-я высших порядков. Дифференциальное уравнение порядка n вида y(n)(х) + p1(x) y(n–1)(х) +… +pn–1(x) y'(х) + pn(x) y(х) = f(x), где коэффициенты уравнения pi(x)(i = 1, 2, ..., n) и правая часть f(x) – заданные функции, а у(х) – неизвестная функция, называется линейным.

Линейное уравнение (1) называется однородным, если f(x) = 0, и неоднородным в противном случае.

Если в линейном дифференциальном уравнении (1) все коэффициенты pi(x) (i = 1, 2, ..., n) и правая часть f(x) непрерывны в интервале (а, b), то при любом х₀ Î (a, b) существует единственное решение, удовлетворяющее начальным условиям: у(х₀) = у₀, у¢(х₀) = у₀1, ..., у(n–1)(х₀) = у₀(n–1).

Сис-мы линей­ных диф ур-ний второго порядка с пост коэффициентами.

Система дифференциальных уравнений

называется системой линейных дифференциальных уравнений с постоянными коэффициентами второго порядка.