
- •Тема 2.1. Введение в математический анализ.
- •Тема 2.2. Функции нескольких переменных.
- •Тема 2.3. Интегральное исчисление функции одной переменной.
- •Тема 2.4. Обыкновенные дифференциальные уравнения.
- •Обыкновенные дифференциальные уравнения.
- •Понятие решения.
- •Дифференциальные уравнения первого порядка.
- •Тема 2.5. Числовые и степенные ряды.
Тема 2.2. Функции нескольких переменных.
Сходимость последовательностей в пространстве An
n-мерным
арифметическим пространством наз
множ-во, сост из всевозможных пронумерованных
чисел от 1до n
(1,2…n). An
–
n-мерное
арифметич пространство. Сост из An=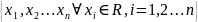 .
Элементы An
– точки (х=(
.
Элементы An
– точки (х=(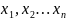 )
или М(
)).
Числа
)
или М(
)).
Числа
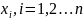 наз координатами точки х или М
наз координатами точки х или М
Расст-е
между точками. Пусть зад 2 точки М(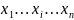 )
и N(
)
и N(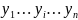 )
)
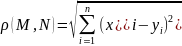
Если
n=2, то
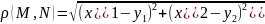
Если
n=3, то
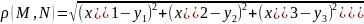
Можно считать, что A2 – обычная плоскость, A3 – обычное 3-х мерное пр-во
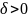 (
(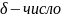 )
)
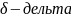
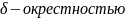 точки
М0(
точки
М0(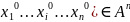 наз множ-во всех точек М с координатами
М(
),
расстояние от к-х до точки М0
строго меньше
наз множ-во всех точек М с координатами
М(
),
расстояние от к-х до точки М0
строго меньше
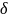 .
.
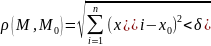
В
n-мерном
пр-ве пара точек М0(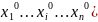 и М1(
)
определяет вектор с началом М0
и концом М1
(
и М1(
)
определяет вектор с началом М0
и концом М1
( )
)
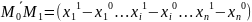
Введенные векторы в n-мерном арифм пр-ве облад всеми св-вами векторов 2-х и 3-х мерного пр-ва.
Понятие функции нескольких переменных.
Пусть
задано произв множ-во
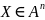 .
Говорят, что на X задана функция от n
переменных, если произв точке М(
)
.
Говорят, что на X задана функция от n
переменных, если произв точке М(
)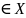 по некоторому правилу ставится в соотв
единственное число Z
по некоторому правилу ставится в соотв
единственное число Z
f
– условное обозначение ф-и от многих
переменных 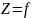 (
)
(
)
Х – обл-ть опред-я ф-ции – там где ф-я определена
Ef – область значений – те числа, к-м в соотв ставятся числа
Ef=
х1, х2… хn – независ-е переем-е (аргументы)
 – ф-я
2 переменных
– ф-я
2 переменных
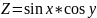
Однородные функции
Функция нескольких переменных наз однородной ф-ей этих переменных степени m, если при умножении этих переменных на произвольную величину t функция умножается на tm, т.е. имеет место тождество:
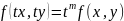 или
или
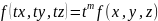 или
или
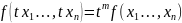 (1)
(1)
при любых допустимых значениях переменных x,y,z,t. Число m может быть любым фиксированным вещественным числом.
Примеры однородных функций:
Однородной
ф-ей третьей степени явл любой однородный
многочлен от x и y третьей степени, т.е.
функция вида
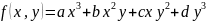
Дроби
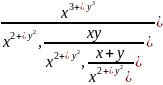 суть однородные ф-ции степеней 1,0 и -1
соответственно
суть однородные ф-ции степеней 1,0 и -1
соответственно
Если
m=0, то, положив в тождестве (1)
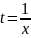 ,
получим
,
получим
 ,
или
,
или
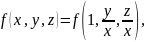 или
или
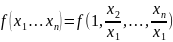 ,
т.е. однородная ф-я нулевой степени есть
ф-я отношения всех переменных, кроме
одной, к этой последней переменной.
Иногда однородную ф-ю нулевого измерения
наз просто однородной.
,
т.е. однородная ф-я нулевой степени есть
ф-я отношения всех переменных, кроме
одной, к этой последней переменной.
Иногда однородную ф-ю нулевого измерения
наз просто однородной.
Предел и непрерывность функции.
Пусть
задана точка
 .
Бесконечная послед-ность точек М1,
М2,…
Мk
.
Бесконечная послед-ность точек М1,
М2,…
Мk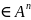 .
Говорят, что данная послед-ть сходится
в т. М0,
если при неогранич увеличении k
.
Говорят, что данная послед-ть сходится
в т. М0,
если при неогранич увеличении k
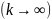

Z=f(M); М( )
Пусть
задана ф-я Z=f(М),
 Задана т
Задана т
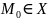 .
Число А наз
пределом данной ф-ции, если для любой
послед-ти точек сходящейся к
.
Число А наз
пределом данной ф-ции, если для любой
послед-ти точек сходящейся к
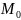 соответствующая послед-ть значений (
соответствующая послед-ть значений (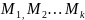 )
функции f(
)
функции f(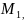 ),
f(
),
f(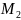 )…
f(
)…
f(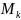 )
имеет своим пределом число А.
)
имеет своим пределом число А.
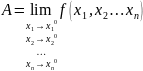 ,
где
,
где

Теорема1.
Пусть заданы 2 ф-ции Z=f(М),
Z=g(М),
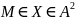 .
Задана точка
.
Если ф-ции f(М),
g(М)
имеют пределы A и B, то имеется предел
ф-ции
.
Задана точка
.
Если ф-ции f(М),
g(М)
имеют пределы A и B, то имеется предел
ф-ции
 ,
при этом
,
при этом

Аналогичные формулы справедливы для функции произведения и частного от 2 переменных. При вычислении предела константа выносится за знак предела.
Непрерывность ф-ции.
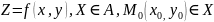
Ф-я Z наз непрерывной в т , если выполняется условие:
Ф-я определена в нек-й окрестности т
В т
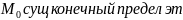 ой
ф-ции
ой
ф-цииПредел ф-ции в данной точке совпад с ее значением в этой точке
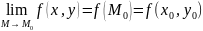
Точки, в к-х нарушается хотя бы одно из условий, наз точками разрыва ф-ции
При исслед ф-ции на непрерывность находят области непрерывности и область точек разрыва.
Ф-я
непрерывна если в области
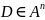 ,
если она непрерывна в каждой точке этой
области.
,
если она непрерывна в каждой точке этой
области.
Частные производные.
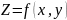 опред
в окрестности точки
опред
в окрестности точки
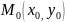
Частной производной (1-го порядка) ф-ции нескольких переменных по одной из этих переменных наз предел отношения соответствующего частного приращения ф-ции к приращению данной переменной, когда последнее стремится к нулю.
Пусть
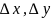 – приращения независимых переменных
x
и y
в некоторой точке
из области X. Тогда величина, равная
– приращения независимых переменных
x
и y
в некоторой точке
из области X. Тогда величина, равная
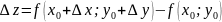 наз полным приращением ф-ции в точке
наз полным приращением ф-ции в точке
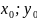 .
Если переменную х зафиксировать, а
переменно у дать приращение
.
Если переменную х зафиксировать, а
переменно у дать приращение
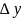 ,
то получим
,
то получим
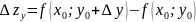 .
Аналогично определяется частная
производная от переменной у.
.
Аналогично определяется частная
производная от переменной у.
Частная
производная по х:
 .
Аналогично опред ч произ от y:
.
Аналогично опред ч произ от y:
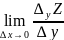 .
Част произв ф-ции
по переем х обазнач:
.
Част произв ф-ции
по переем х обазнач:
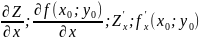 .
Аналогично для y.
.
Аналогично для y.
Правило
вычисл-я ч произв: Т.к. при вычисл ч произв
по перем х знач-е перем y счит фиксир, то
отнош
 явл ф-ей завис от х.
явл ф-ей завис от х.
Т.о. вычисл-е ч произв по х сводится к вычисл произв ф-ции 1 переменной, завис от х, при этом y=const
Для
функции ![]() одной
переменной производная n–го
порядка определялась следующим
образом:
одной
переменной производная n–го
порядка определялась следующим
образом: ![]() .
Аналогично определяются и частные
производные высших порядков.
.
Аналогично определяются и частные
производные высших порядков.
Частной производной n–го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n–1–го порядка той же функции.

Частная производная 2–го или более высокого порядка, взятая по нескольким различным переменным, называется смешенной частной производной.
Справедлива теорема:
Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.
Так, ![]()
Полный дифференциал и его применение в приближенных вычислениях.
Полное
приращ ф-ции
опред
в окрестности точки
– разность
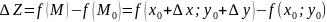
Если
полное приращ ф-ции
в т
представимо в виде
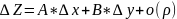 (1) ,
то ф-я наз дифференцируемой ф-ей в т
(1) ,
то ф-я наз дифференцируемой ф-ей в т
Гл
часть
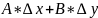 –
дифференциал ф-ции в данной точке
–
дифференциал ф-ции в данной точке
В
ф-ле (1) A и B – const,
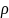 – расстояние между точками M
и M0
– расстояние между точками M
и M0

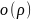 – бесконечно малое более высокого
порядка чем
.
– бесконечно малое более высокого
порядка чем
.
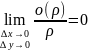
Дифференциал
ф-ции:
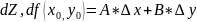
Теорема. Дифференциал ф-ции в т вычисл след обр
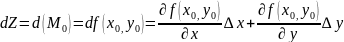 .
Если ввести обознач
.
Если ввести обознач
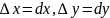 ,
то
,
то
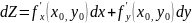 (2) Ф-ла
(2) опред дифференциал в заданной точке
(2) Ф-ла
(2) опред дифференциал в заданной точке
Док-во:Пусть
диференцируема в точке
.
Тогда полное приращ
.
Положим
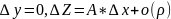
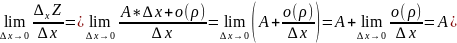
Из
этого следует, что A= .
Аналогичным образом доказывается, что
B
в ф-ле дифференциала (2)=
.
Аналогичным образом доказывается, что
B
в ф-ле дифференциала (2)=
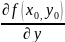
Полный
дифференциал и его применение в
приближенных вычислениях.
диференцируема в точке
,
т.е. сущ
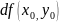 .
Придадим приращение
соответствующие x,y.
Получим точку (
.
Придадим приращение
соответствующие x,y.
Получим точку (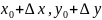 )
)
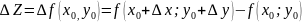 .
Т.к. ф-я дифференц, то:
.
Т.к. ф-я дифференц, то:
 .
Отбрасывая
в данной ф-ле, получим приближ рав-во:
.
Отбрасывая
в данной ф-ле, получим приближ рав-во:
 ,
при
–
достат
малые
,
при
–
достат
малые
Производная функции по направлению. Градиент функции и его свойства.
Производная
функции
в
точке M в
направлении вектора
в
направлении вектора ![]() называется
называется ![]() ,
где
,
где ![]() .
.
Если
функция ![]() дифференцируема,
то производная в данном направлении
вычисляется по формуле
дифференцируема,
то производная в данном направлении
вычисляется по формуле ![]() ,
где
,
где 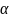 ,
,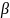 -
углы, образованные вектором
-
углы, образованные вектором 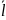 с
осями Ox
и Oy.
с
осями Ox
и Oy.
П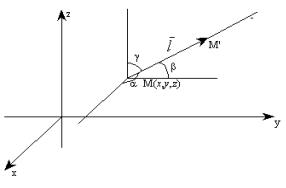 роизводная
по направлению
роизводная
по направлению ![]() дает
скорость изменения функции
Z в
направлении вектора
.
дает
скорость изменения функции
Z в
направлении вектора
.
Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).
Как известно, проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению.
Градиент функции в данной точке указывает напрвление наиболее быстрого возрастания функции.
Величина
градиента, т.е. | grad u | = обозначается
tg j и определяет крутизну наибольшего
ската или подъема поверхности u = f (x, y).
обозначается
tg j и определяет крутизну наибольшего
ската или подъема поверхности u = f (x, y).
Градиентом
функции
наз
вектор, проекциями к-го на координатные
оси явл соотв частные производные
функции
Z:
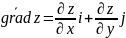 . Производная ф-ции в направлении l
связана с градиентом ф-ции след формулой:
. Производная ф-ции в направлении l
связана с градиентом ф-ции след формулой:
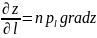 , т.е. производная в данном направлении
равна проекции градиента ф-ции на
направление дифференцирования.
, т.е. производная в данном направлении
равна проекции градиента ф-ции на
направление дифференцирования.
Градиент
ф-ции в каждой точке направлен по нормали
к соотв линии ур-ня ф-ции. Направление
градиента ф-ции в данной точке есть
направление наибольшей скорости
возрастания ф-ции в этой точке, т.е. при
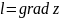 производная
производная
 принимает наибольшее значение, равное
принимает наибольшее значение, равное
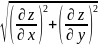 . Аналогично опред градиент функции 3
переменных u = f(x,
y,
z):
. Аналогично опред градиент функции 3
переменных u = f(x,
y,
z):
 . Градиент функции 3 переменных в каждой
точке направлен по нормали к поверхности
ур-ня, проходящей через точку.
. Градиент функции 3 переменных в каждой
точке направлен по нормали к поверхности
ур-ня, проходящей через точку.
Экстремум функции двух и более переменных.
Пусть
функция
определена
в некоторой области D
и точка 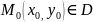 .
.
Функция
имеет
в точке
локальный
максимум,
если существует такая окрестность этой
точки, что для всех точек M (x,
y) этой
окрестности выполняется неравенство 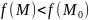 .
.
Функция
имеет
в точке
локальный
минимум,
если существует такая окрестность этой
точки, что для всех точек M (x,
y) этой
окрестности выполняется неравенство  .
.
Максимум и минимум функции называются экстремумами функции.
Необходимые и достаточные условия.
Теорема (необходимое условие экстремума). Если ф-я диференцируема в окрестности точки и в этой точке сущ экстремум ф-ции, то частные произв ф-ции по обоим переменным в этой точке =0.
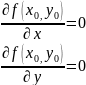
Замечание 1. Если ф-я u = f(x, y, z), то необход условием сущ экстремума ф-ции в точке явл рав-во нулю всех ее частных производных в этой точке.
Таким обр первый этап нахождения экстремума ф-ции сост в нахожд стацион точек.
Не дифференцир ф-я может принимать экстремальные значения в точках, в к-х производная не сущ.
Теорема(достаточное условие экстремума).
Пусть функция определена в некоторой окрестности точки и имеет в этой окрестности непрерывные частные производные до второго порядка включительно. Если выполняются условия:
1)
частные производные первого порядка в
точке
равны
нулю:
 .
.
.
.
2)
для чисел
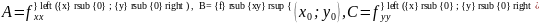 выполняется
неравенство:
выполняется
неравенство:
а)
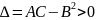 ,
то в точке функция имеет экстремум,
причем минимум, если A>0
и максимум, если A<0
,
то в точке функция имеет экстремум,
причем минимум, если A>0
и максимум, если A<0
б)
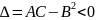 ,
то в этой точке экстремума нет.
,
то в этой точке экстремума нет.
Если Δ=0, то нужны дополнительные исследования.
Условный экстремум и методы его отыскания.
f(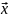 )
)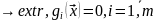 .
Ф-ции f(
)
и
.
Ф-ции f(
)
и
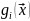 непрерывны вместе со своими производными.
непрерывны вместе со своими производными.
Точка
 наз точкой условного локального
экстремума, если при некотором
выполняется
наз точкой условного локального
экстремума, если при некотором
выполняется
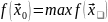 при
при
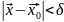
Пусть
дана ф-я
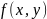 2 переменных при заданном уравнении
связи
2 переменных при заданном уравнении
связи
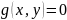
Для нахождения условного экстремума вводится ф-я Лагранжа
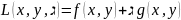 ,
где
,
где
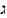 -
множитель Лагранжа, и затем исследуют
ее на безусловный экстремум.
-
множитель Лагранжа, и затем исследуют
ее на безусловный экстремум.
Записывая
необходимое условие экстремума для
ф-ции Лагранжа, получаем след:
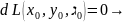
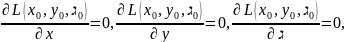 (1)
(1)
Достат
условие. Пусть
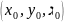 удовлетворяет уравнениям (1) (стационарная
точка ф-ции Лагранжа): если
удовлетворяет уравнениям (1) (стационарная
точка ф-ции Лагранжа): если
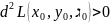 ,
то в точке
,
то в точке
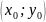 – условный локальный минимум, если
– условный локальный минимум, если
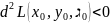 ,
то в точке
– условный локальный максимум.
,
то в точке
– условный локальный максимум.
Замечание.
Нужно иметь ввиду, что дифференциалы
переменных dx и dy в
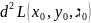 зависимы, и эта зависимость диктуется
уравнением связи. При определении знака
величины d
не учитываются, т.е. полагается
зависимы, и эта зависимость диктуется
уравнением связи. При определении знака
величины d
не учитываются, т.е. полагается
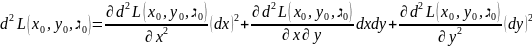
Выравнивание эмпирических данных по прямой и параболе.
Выравнивание экспериментальных данных по прямой
Пусть
для данных табл. 1.1 из теоретических или
практических соображений известно, что
эмпирическую функцию следует искать в
виде
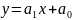 .
Тогда наилучшие значения параметров
.
Тогда наилучшие значения параметров
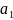 и
и
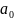 являются
решением нормальной системы метода
наименьших квадратов, которая в данном
случае имеет вид:
являются
решением нормальной системы метода
наименьших квадратов, которая в данном
случае имеет вид:
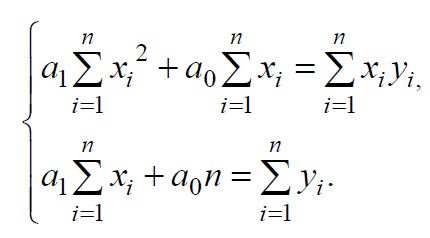
Выравнивание экспериментальных данных по параболе
Пусть
экспериментальные данные из табл. 1.1
располагаются вблизи некоторой параболы
так, что между переменными x
и y
можно предположить наличие зависимости,
которая выражается формулой
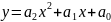 .
Тогда,
следуя методу наименьших квадратов,
надо найти минимум по
.
Тогда,
следуя методу наименьших квадратов,
надо найти минимум по
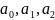 функции
трех переменных
функции
трех переменных
![]()
Вычисляя
частные производные
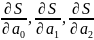 и
приравнивая их к нулю, получаем нормальную
систему метода наименьших квадратов
при выравнивании по параболе:
и
приравнивая их к нулю, получаем нормальную
систему метода наименьших квадратов
при выравнивании по параболе:
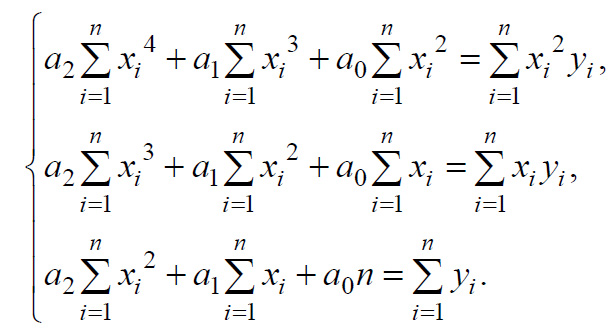
Решая
эту систему, находим требуемые
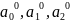 ,
так что искомое уравнение квадратичной
зависимости есть
,
так что искомое уравнение квадратичной
зависимости есть
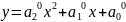 .
.
Метод наименьших квадратов.
Важное значение имеет следующая задача: требуется установить вид функциональной зависимости между двумя переменными величинами x и y по результатам n экспериментальных измерений, приведенных в таблице 1.1:
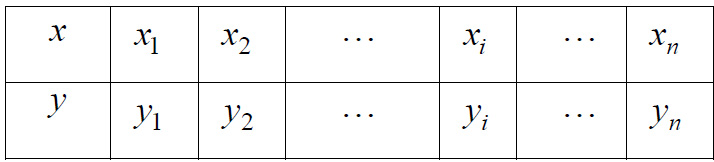
Иначе говоря, требуется выразить зависимость между x и y аналитически, т.е. указать формулу, связывающую между собой соответствующие значения переменных. Формулы, служащие для аналитического представления опытных данных, принято называть эмпирическими формулами.
Исходя
из некоторых теоретических или
практических соображений (например,
конфигурации расположения точек на
координатной плоскости) подбирается
наиболее простая формула, которая дает
наилучшее совпадение с опытными данными.
Наиболее типичными в экономических
исследованиях являются формы зависимостей
в виде линейной
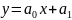 ,
квадратичной
,
квадратичной
 ,
степенной
,
степенной
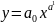 , логарифмической
, логарифмической
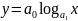 ,
показательной
,
показательной
 и
обратно-пропорциональной
и
обратно-пропорциональной
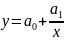 функций. Слова «наилучшее совпадение»
понимаются здесь в том смысле, что из
данного множества формул вида
функций. Слова «наилучшее совпадение»
понимаются здесь в том смысле, что из
данного множества формул вида
 наилучшей
считается та, для которой сумма квадратов
отклонений наблюдаемых значений
наилучшей
считается та, для которой сумма квадратов
отклонений наблюдаемых значений
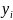 от
вычисленных по формуле значений
от
вычисленных по формуле значений
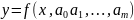 является наименьшей. Описанный третий
способ построения эмпирической формулы
называется методом
наименьших квадратов,
а вычисленные путем решения задачи
является наименьшей. Описанный третий
способ построения эмпирической формулы
называется методом
наименьших квадратов,
а вычисленные путем решения задачи
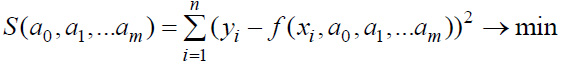
значения
параметров
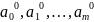 задают
наилучшую в смысле метода наименьших
квадратов формулу
задают
наилучшую в смысле метода наименьших
квадратов формулу
 .
Исходя
из необходимых условий экстремума
функций многих переменных, минимум
функции S
.
Исходя
из необходимых условий экстремума
функций многих переменных, минимум
функции S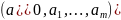 будет
в тех точках, где частные производные
будет
в тех точках, где частные производные
 обращаются
в нуль. Таким образом, получается система
(m+1)
уравнений с (m+1)
неизвестными
обращаются
в нуль. Таким образом, получается система
(m+1)
уравнений с (m+1)
неизвестными
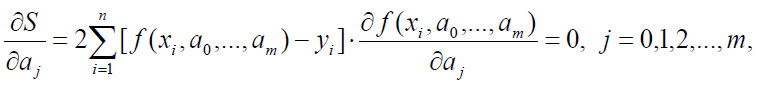
именуемую нормальной системой метода наименьших квадратов.
