Тема 2.1. Введение в математический анализ.

Дифференциальное исчисление функции одной переменной

Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций.

Понятие числовой последовательности

Если каждому числу n из множества N поставлено соответственно некоторое вещественное число X_n , то упорядоченное множество {x₁, x₂, x₃…x_n…} называется числовой последовательностью.

Виды последовательностей.

Критерий ограниченности числовой последовательности

Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.

Ограниченная сверху последовательность — это последовательность элементов множества Х, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

Ограниченная снизу последовательность — это последовательность элементов множества Х, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.

Неограниченная последовательность — это последовательность, которая не является ограниченной.

Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

Последовательность, у которой существует конечный предел, называется сходящейся. Если никакое число не является пределом последовательности, то она называется расходящейся.

Последовательность {x_n} называется возрастающей, если для любого n N выполняется неравенство

x_n + 1 > x_n. Последовательность {x_n} называется убывающей, если для любого n N выполняется неравенство x_n + 1 x_n. Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей. Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называют монотонными.

Сходящиеся последовательности и их свойства.

Последовательность {x_n} называется сходящейся, если существует такое вещественное число а, что последовательность {x_n−a} является бесконечно малой.

Если последовательность {x_n→a } является сходящейся и имеет своим пределом число a, то символически это записывают так: 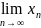= a.

Св-ва:

1. Сходящаяся последовательность имеет только один предел.

2. Всякая сходящаяся последовательность является ограниченной. Но Не всякая ограниченная последовательность является сходящейся.

3. Сумма сходящихся последовательностей {x_n} и {y_n} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {x_n} и {y_n}.

4. Разность сходящихся последовательностей {x_n} и {y_n} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {x_n} и {y_n}

5. Произведение сходящихся последовательностей {x_n} и {y_n} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {x_n} и {y_n}.

6. Частное двух сходящихся последовательностей {x_n} и {y_n}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {x_n} и {y_n}.

Теоремы о пределах последовательностей

Число А называется пределом последовательности , если для любого 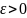существует число , такое, что при 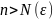выполняется неравенство .

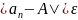Число 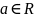называется пределом {x_n}, если с ростом n 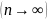величина x_n неограниченно приближается к при .

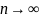1. Последовательность, имеющая предел, ограничена.

2. Последовательность может иметь только один предел.

3. Любая неубывающая (невозрастающая) и ограниченная сверху (снизу) последовательность имеет предел.

4. Предел постоянной равен этой постоянной:

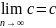
5. Предел суммы равен сумме пределов:

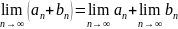
6. Постоянный множитель можно выносить за знак предела:

7. Предел произведения равен произведению пределов:

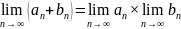
8. Предел частного равен частному пределов, если предел делителя отличен от нуля: ;

9. Если 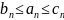и обе последовательности {b_n} и {c_n} имеют один и тот же предел а, то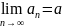

Числовые множества

1. Множество натуральных чисел N = {1,2,3,4,…..n,…..}

2. Множество целых чисел Z = {0, ±1,±2, ±3, …..±n,….}

3. Множество рациональных чисел Q =

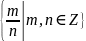
4. Множество действительных чисел R . Множество R содержит рациональные и иррациональные числа.

Числовые промежутки. Окрестность точки.

Интервал (a,b) =

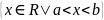
Отрезок

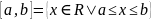
Полуинтервал

Полуинтервал

Окрестностью точки х₀ называется любой интервал (a; b), содержащий точку х₀. В частности, интервал (х₀-e, х₀+e), где e > 0, называется e - окрестностью точки х_0.

Понятие функции одной переменной

Пусть заданы множества X,Y R. Говорят на Х определена f со значениями Y, если для 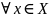по некоторому правилу f ставится в соответствие единственное число y Y. Обозначается y = f(x). х – независимая переменная, у – зависимая.

Область определения, способы задания функции.

Х называется областью определения функции, Y – областью значений. Для того чтобы для y = f(x) найти область определения надо из множества R удалить те значения х, для которых невозможно вычислить у. Невозможность вычисления исходит из невозможности выполнения арифметических или других операций.

Способы задания функции:

1) аналитический - задается формулой

2) графический – задается графиком

3) табличный – задается таблицей

4) описательный – задается словесным описанием

Основные характеристики функции одной переменной

1. Четность. Функция y=f(x) называется четной, если f(-x) = f(x), при этом х ОДЗ. Функция y=f(x) называется нечетной, если f(-x) = -f(x), при этом х ОДЗ.

2. Периодичность. Функция y=f(x) называется периодической с периодом Т 0, если для любого х из области определения значения х+Т и х-Т также принадлежат области определения и f(x) = f(x+T) = f(x-T)

3. Монотонность (возрастание, убывание). Функция у=f(x) называется возрастающей на интервале (а,b), если для любых х₁ и х₂ из этого интервала таких, что х₁ х₂ , справедливо неравенство f(x₁) f(x₂). Функция у=f(x) называется убывающей на интервале (а,b), если для любых х₁ и х₂ из этого интервала таких, что х₁ х₂ , справедливо неравенство f(x₁) f(x₂).

4. Экстремумы (максимумы и минимумы). Внутренняя точка х_max области определения называется точкой максимума, если для всех х из некоторой окрестности этой точки справедливо неравенство f(x) f(x_max ). Значение y_max = f(x_max ) называется максимумом этой функции. Внутренняя точка х_min области определения называется точкой минимума, если для всех х из некоторой окрестности этой точки справедливо неравенство f(x) f(x_min). Значение y_min = f(x_min ) называется минимумом этой функции.

5. Выпуклость, вогнутость. Функция f ( x ) называется выпуклой на интервале ( a, b ), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f ( x ) в любой точке ( x₀ , f ( x₀ ) ), x₀ ( a, b ). Функция f ( x ) называется вогнутой на интервале ( a, b ), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f ( x ) в любой точке ( x₀ , f ( x₀ ) ), x₀ ( a, b ).

Основные элементарные функции

1. Постоянная у = с, с = const R

2. Степенная

3. Показательная

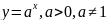
4. Логарифмическая

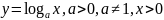
5. Тригонометрические

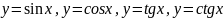
6. Обратные тригонометрические y = arcsin x, y = arccos x, y = arctg x, y = arcctg x

Понятие предельной точки множества

Точка x называется предельной точкой подмножества A в топологическом пространстве X , если всякая проколотая окрестность точки x имеет с A непустое пересечение.

Для пространств X, у которых все точки (одноточечные множества) замкнуты, есть равносильное определение: Точка x называется предельной точкой подмножестваA, если всякая окрестность точкиxимеет с Aбесконечное число общих точек.

Предел функции в точке

Пусть задана Z=f(х;у), тогда А – предел ф-ции в т.(х0,y0), если для любого сколь угодно малого положит. числа E>0 сущ-т полож-е число б>0, что для всех х,у удовл-щих |x-х0|<б; |y-y0|<б выполняется нерав-во |f(x,y)-A|<E

Предел функции на бесконечности

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.

Предел на бесконечности по Коши

Пусть числовая функция f(x) задана на множестве X , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного d в нём найдётся элемент, лежащий за границами отрезка [-d,+d] . В этом случае число A называется пределом функции f(x) на бесконечности, если для произвольного положительного числа e отыщется отвечающее ему положительное число dакое, что для всех точек, превышающих d по абсолютному значению, справедливо неравенство

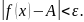
Пусть числовая функция f(x) задана на множестве X , в котором для любого числа d найдётся элемент, лежащий правее него. В этом случае число A называется пределом функции f(x) на плюс бесконечности, если для произвольного положительного числа e отыщется отвечающее ему положительное число d такое, что для всех точек, лежащих правее d , справедливо неравенство

Пусть числовая функция f(x) задана на множестве X , в котором для любого числа d найдётся элемент, лежащий левее него. В этом случае число A называется пределом функции f(x) на минус бесконечности, если для произвольного положительного числа e отыщется отвечающее ему положительное число dтакое, что для всех точек, лежащих левее (-d) , справедливо неравенство

Односторонний предел - это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.

Бесконечно малые и бесконечно большие функции

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M.

Основные правила вычисления пределов

Пусть — действительная константа и — целое положительное число. При условии,что существуют оба предела и , имеют место следующие десятьосновных правил для вычисления пределов. Правила даны в форме двустороннего

предела, но они остаются в силе и при вычислении односторонних пределов.

Правило суммы и разности: .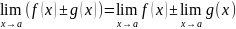

Правило постоянного множителя: .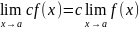

Правило произведения: .

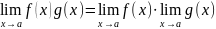Правило отношения: 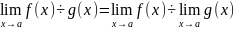, если .

Правило константы: .

Правило степени: .

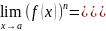Правило корня: .

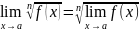Замечательные пределы

Первый : Второй:

Непрерывность функции в точке и на множестве

Z=f(х;у) непрерывна в т.(х0,y0), если: - она опред-на в этой т.; - имеет конеч. предел при х, стрем-ся к х0 и у к у0; - этот предел = знач-юф-ции в т.(х0,y0), т.е. limf(х;у)=f(х0,y0)

Если ф-ция непрерывна в кажд. т. мн-ва Х, то она непрерывна в этой области

Точки в которых нарушается условие называются точками разрыва данной функции

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

-Существуют левосторонний предел и правосторонний предел ;

-Эти односторонние пределы конечны.

При этом возможно следующие два случая:

-Левосторонний предел и правосторонний предел равны друг другу:

Такая точка называется точкой устранимого разрыва.

-Левосторонний предел и правосторонний предел не равны друг другу:

Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов называется скачком функции.

Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.

Свойства функций непрерывных на отрезке:

1. Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.

2. Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем m £ f(x) £ M

3. Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.

4. Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.

5. Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.

Производная функции – основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

Геометрический смысл: Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Механический смысл: производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).

Экономический смысл: Рассмотрим задачу о производительности труда. Пусть функция и = и (t) отражает количество произведенной продукции u за время ti необходимо найти производительность труда в момент t0. Производительность труда есть производная от объема произведенной продукции по времени.

Непрерывность функции, имеющей производную

Пусть функция f(x) дифференцируема (дифференцируема слева, дифференцируема справа) в точке x0 . Тогда f(x) непрерывна (соотв. непрерывна слева, непрерывна справа) в этой точке x0.

Правила дифференцирования.

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v2;

5) если y = f(u),u = j(x), т.е. y = f(j(x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций j и f, то , или ;

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем ≠ 0, то .

Логарифмическая произво́дная — производная от натурального логарифма функции.

часто применяется для упрощения нахождения производной некоторых функции, например сложнопоказательных.

Производная неявной функции

y=y(x) задана не явно , если она определена F(x,y)=0 гдеF(x,y) некоторая дифферен-ая функция

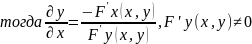
Производные основных элементарных функций

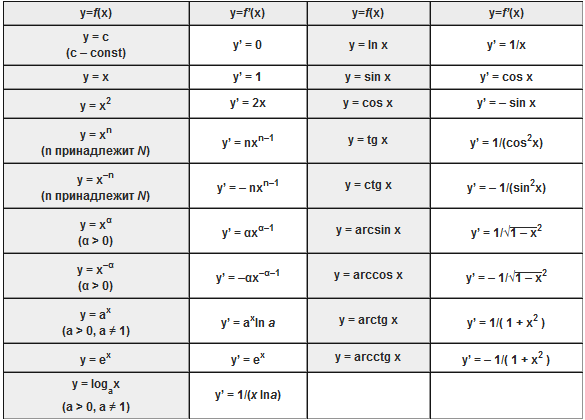
Производные высших порядков

Пусть функция y=f(x) дифференцируема на множестве Х. Производная f'(x) этой функции является функцией от х на Х. Следовательно, можно говорить о производной полученной функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции у= f(x) или , короче, второй производной и обозначают f''(x) или у''.

Понятие дифференциала функции в точке. Геометрический смысл дифференциала.

В настоящее время дифференциал чаще всего рассматривают как вторичное понятие, тесно связанное и определяемое через понятие производной.

Определение 8.8. Пусть функция у = f (х) определена в некоторой окрестности точки х₀. Функция f (х) называется дифференцируемой в точке х₀, если ее приращениe в этой точке можно представить в виде

(8.10)

где A (х₀) не зависит от , бесконечно малая при . Линейная относительно часть приращения функции в точке х₀ называется дифференциалом функции в точке х₀ и обо­значается df(х₀)или dy.

Если приращение аргумента обозначить через dx и назвать дифференциалом независимой переменной х, то дифферен­циал запишется в видеdy=A(х₀)dx.

Теорема 8.6. Для того, чтобы функция у = f (х) была дифферен­цируема в некоторой точке х₀, необходимо и достаточно, чтобы она имела в этой точке производную f'(х₀), при этом и (8.11)

Замечание. Разделив обе части выражения (8.11) на dх, получа­ется обозначение для производной (8.12)

До сих пор обозначение имело символический характер; сейчас это выражение можно рассматривать как дробь с числителем dу и знаменателем dх (отношение дифференциалов).

Формула (8.11) позволяет находить дифференциалы функций, ес­ли известны их производные и выписать по таблице производных таблицу дифференциалов.

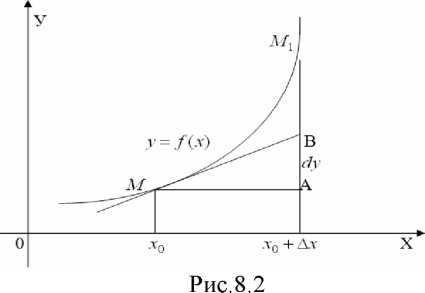
Геометрический смысл значения дифференциала в точке х₀ - это приращение ординаты касательной в этой точке при переходе к точке . На рис. 8.2. дифференциал равен отрезку AB.

Замечание. Если сопоставить определения производной и диф­ференциала, то можно заключить, что производная характеризует скорость изменения функции в рассматриваемой точке, а дифферен­циал доставляет наилучшую линейную аппроксимацию приращения функции в окрестности рассматриваемой точки. Строение дифферен­циала теоретически проще и практически удобнее, чем строение при­ращения функции — дифференциал dу есть линейная функция, опре­деленная на смещениях от рассматриваемой точки. Этот факт удобно использовать для вычисления приближенных значений функций.

Если предположить, что функция у=f(х) является сложной функцией, т.е. х=g(t), и, следовательно, у=f(g(t))≡g(t), то про­изводная (8.12) примет вид и тогда выражение для дифференциала (8.11) перепишется в виде , так как

Такое свойство дифференциала — равенство дифференциала про­изведению производной по некоторой переменной на дифференциал этой переменной (независимо от того, является ли эта переменная не­зависимой или, в свою очередь, функцией другой независимой пере­менной) - называется инвариантностью формы первого диффе­ренциала относительно выбора переменных.

Применение дифференциала к приближенным вычислениям.

Из равенств (8.10) и (8.11) следует, что являет­ся бесконечно малой более высокого порядка, чем . Значит, справедливо приближенное равенство или, в подробной записи,

(8.13)

Это равенство часто используется при приближенных расчетах. Для вычисления значения функции в точке берут в некоторой достаточно малой ее окрестности такую точку х₀, чтобы f(х₀ ) и f'(х₀ ) вычислялись легко.

Основные теоремы о дифференцируемых функциях.

Теорема 8.7 (Ферма). Пусть функция у=f(х) определена на некотором интервале (a, b) и в точке принимает наибольшее или наименьшее значение. Если существует производная в этой точке f'(c), то она необходимо равна нулю: f'(c) = 0.

Геометрически — касательная к графику в точке локального экстремума параллельна оси Ох, так как k_кас=f’(c)=0.

Теорема 8.8 (Ролля). Пусть функция f (х) удовлетворяет сле­дующим условиям:

1. непрерывна на отрезке [a, b];

2. имеет производную на интервале

3. на концах интервала принимает равные значения: f(a)=f(b). Тогда существует точка 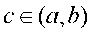, такая, что f'(c) = 0.

Геометрический смысл теоремы Ролля заключается в том, что на графике функции, удовлетворяющем условию теоремы, обязательно существует точка (по крайней мере, одна ) в которой касательная к графику параллельна оси Ох.

Теорема 8.9 (Лагранжа). Пусть функция у=f(х) непрерывна на отрезке [a,b] и имеет производную в каждой точке интервала (a, b). Тогда существует такая точка , что

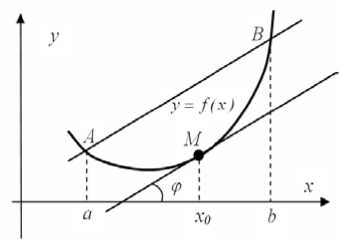
(8.14)

Если в равенстве (8.14) обозначить (c-a)/(b-a)=λ, откуда c=a+λ(b-a), где 0<λ<1 (ведь A<c<b), то (8.14) перепишется в виде

(8.15)

Положим теперь Тогда (8.16)

Формула (8.16) называется формулой конечных приращений в от­личие от приближенного равенства , кото­рое называется формулой бесконечно малых приращений.

Теорема 8.10 (Коши). Пусть функции f(х) и g(х) непрерывны на отрезке [a,b] и имеют производные в каждой точке интервала (a,b), причем для всех Тогда существует такая точка , что (8.17)

Формула (8.17) называется обобщенной формулой конечных при­ращений Коши.

Правило Лопиталя раскрытия неопределенностей.Используем понятие производной для раскрытия неопределенностей.

Теорема 8.11. Пусть имеется частное двух функций f(x)/g(x), где функции f(х) и g(х) определены в промежутке [a, b], имеют конечные производные f'(x) и g'(x) в этом промежутке, за исключением быть может точки х=a, причем . Тогда, если обе функции бесконечно малые или бесконечно большие при , т.е. если частное f(x)/g(x) при представляет неопределенность 0/0 или ∞/∞ то

(8.18)

Правило (8.18) применимо в тех случаях, когда предел отношения производных существует. Правило применимо и в тех случаях, когда a=∞.

Раскрытие неопределенностей ∞-∞, 0-∞ и 0⁰, ∞⁰ , 1^∞ тоже можно осуществлять с помощью правила Лопиталя, если только пре­образовать выражения к виду 0/0 и ∞/∞ с помощью алгебраических преобразований и логарифмирования.

Заметим, что правило Лопиталя применимо только тогда, когда справедливы условия теоремы, т.е. когда существует предел отношения производных.

Условия постоянства, возрастания и убывания функций.

Теорема 8.12. Пусть функция у=f(х) имеет конечную произ­водную при . Для того, чтобы эта функция сохраняла посто­янное значение f(х)=const при , необходимо и достаточно выполнения условия f' (х) = 0 при .

Теорема 8.13. Пусть функция у = f(х) дифференцируема на ин­тервале (a, b). Тогда если f'(х)>0 на (a, b), то f(х) строго возрас­тает на (a, b); если же f'(х) < 0 ,то f (х) строго убывает на (a, b).

Необходимые и достаточные условия экстремума функции.

Определение 8.12. Пусть функция у=f(х) определена в некото­рой окрестности точки х₀. Точка х₀ называется точкой максимума (минимума) функции f(х), если существует такое , что для всех , удовлетворяющих условию , выполняется неравен­ство . Если существует такое , , что для всех , удовлетворяющих условию , выполняется неравенство , то точка х₀ называется точкой строгого макси­мума (минимума). Точки максимума и минимума называются точ­ками экстремума.

Теорема 8.14 (необходимое условие экстремума). Если функция f(х) определена в некоторой окрестности точки х₀ и точка х₀ является точкой экстремума функции f(х), то либо производная f' (х₀) обращается в нуль, либо не существует.

Простые примеры показывают, что эти необходимые условия экстремума не являются достаточными.

Теорема 8.15 (первое достаточное условие экстремума). Пусть функция f(х) дифференцируема в окрестности точки , за исключением может быть самой точки х₀ , в которой она является непрерывной. Тогда:

а) если f'(х) > 0 при х < х₀ и f'(х) < 0 при х > х₀, то х₀ — точка строгого максимума;

б) если f' (х) < 0 при х < х₀ и f'( х) > 0 при х > х₀, то х₀ — точка строгого минимума;

в) если f'(х) в окрестности точки х₀ не меняет знак, то экстремума нет.

Коротко можно сказать, что если производная f'(х) при переходе через точку х₀ меняет знак с плюса на минус, то х₀ - точка строгого максимума, а если с минуса на плюс, то х₀ - точка строго минимума. Заметим сразу же, что эти условия, являясь достаточными, не являются необходимыми для экстремума. Иногда вызывает затруднение иссле­дование знака первой производной в окрестности заданной точки.

В ряде случаев бывает удобным применить при изучении точек экстремума следующую теорему.

Теорема 8.16 (второе достаточное условие экстремума). Пусть в точке х₀ для функции f(х) выполняются условия:

f'(х₀) = 0, . Тогда, если f''(х₀) > 0, то f (х) имеет в точке х₀ строгий минимум; если f"( х₀) < 0, то f(х) имеет в точке х₀ строгий максимум.

Выпуклость и вогнутость графика функции.

Определение 8.13. График функции называется выпуклым (или говорят еще выпуклым вверх) на отрезке [a, b], если он расположен ниже любой своей касательной на этом отрезке (рис. 8.3).

В этом случае выполняется неравенство

Определение 8.14. График функции называется вогнутым (гово­рят еще выпуклым вниз) на отрезке [a, b], если он расположен выше любой своей касательной на этом отрезке (рис.8.4). В этом случае

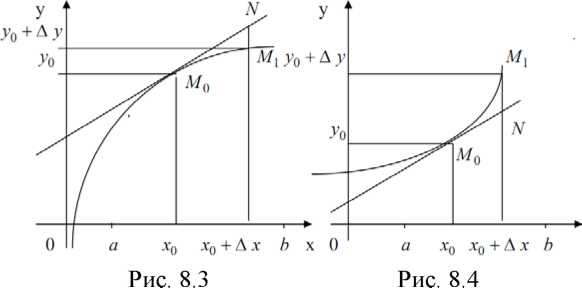
Определение 8.15. Точки графика, в которых выпуклость меняет­ся на вогнутость, называются точками перегиба.

Теорема 8.17. Пусть функция f(х) дважды дифференцируема на интервале (a, b). Тогда, если f"(х) < 0 на (a, b), то функция f(х) выпукла на этом интервале, а если f"(х) > 0 на интервале (a, b), то функция f (х) вогнута на этом интервале.

Теорема 8.18. Если функция f(х) дважды непрерывно дифференцируема на интервале (a, b) и точка х₀ из этого интервала является точкой перегиба, то выполняется неравенство f"(х) = 0 .

Теорема 8.19. Если функция f(х) дважды дифференцируема в некоторой окрестности точки х₀, за исключением может быть самой точки х₀, в которой функция f(х) непрерывна, то, если вторая производная f"(х) меняет знак при переходе аргумента х через точку х₀ , то точка х₀ является точкой перегиба функции.

Определение 8.16. Точки, в которых вторая производная равна нулю или не существует, называются критическими точками по вто­рой производной.

Асимптоты графика функции.Определение 8.17. Прямая L называется асимптотой кривой у = f (х), если расстояние между точками кривой и прямой стремится к нулю при неограниченном удалении точки от начала координат, т.е. . Прямая у= kх + b называется наклонной асимптотой графика у = f (х) .

Теорема 8.20. Для того, чтобы прямая у= kх + b была наклонной асимптотой графика у = f (х), необходимо и достаточно, чтобы существовали пределы

(8.19)

Определение 8.18. Если k=0, то асимптота у=b называется го­ризонтальной.

Определение 8.19. Пусть функция у=f(х) определена в некото­рой окрестности точки х₀ (может быть односторонней) и пусть хотя бы один из односторонних пределов равен бесконечности, т.е.

(8.20)

Тогда прямая х=х₀ называется вертикальной асимптотой функции у=f(х)

Общая схема исследования функций и построения графиков.

Для исследования функции и построение ее графика с помощью производной можно рекомендовать следующую схему:

1. Найти область определения функции.

2. Установить, является ли функция четной, нечетной или обще­го вида.

3. Установить, является ли функция периодической.

4. Исследовать функцию на непрерывность и установить харак­тер точек разрыва, найти вертикальные асимптоты.

5. Найти точки пересечения с осями координат и установить промежутки знакопостоянства.

6. Вычислить первую производную, найти точки, где она равна нулю или не существует (критические точки по первой производной), разбить область определения этими точками и определить участки возрастания, убывания и точки экстремума.

7. Вычислить вторую производную, найти точки, где она равна нулю или не существует (критические точки по второй производной) и определить точки выпуклости и вогнутости функции и точки пере­гиба.

8. Найти наклонные и горизонтальные асимптоты и начертить график, при необходимости вычислить несколько дополнительных точек графика.

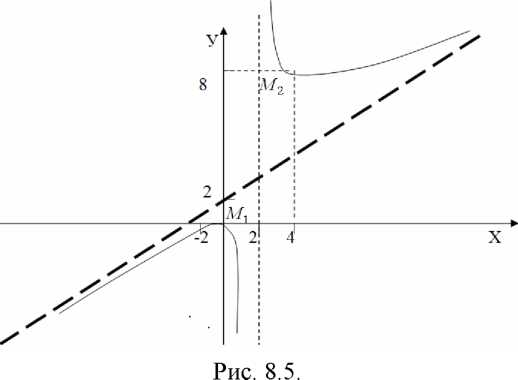
Пример 8.15. Построить график функции

1) Находим область определения функции:

2-3) Так как область определения несимметрична относительно начала координат, то функция свойством четности и нечетности, а также периодичности, не обладает.

4) Во всех точках области определения функция непрерывна, как элементарная функция. Так как , , то х=2 является точкой разрыва второго

рода. Прямая х=2 является вертикальной асимптотой графика.

5) Находим точки пересечения с осями координат: если х=0, то у=0; если у=0, то Откуда получаем х=0 . Значит, график проходит через начало координат и у>0, если х>2; у<0, если

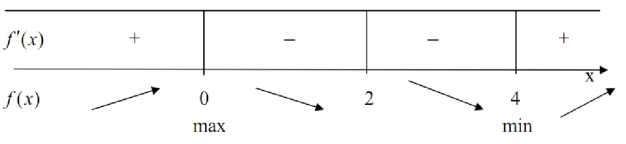
6) Находим первую производную

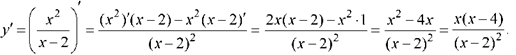
Решая уравнение х1=0, х2=4, находим критические точки по первой производной: х=0 и х=4 .

В окрестности точки х=0 производная меняет знак с плюса на минус. Это означает, что х=0 — абсцисса точки максимума. Тогда и следовательно M₁(0,0) — точка максимума. В

окрестности точки x=4 производная меняет знак минуса на плюс, значит х=-4 — абсцисса точки минимума, , M₂ (4,8) - точка минимума. Таким образом, на интервалах (-∞,0) и на (4,+ ∞) функция возрастает, а на интервалах (0; 2) и (2; 4) — убывает.

7) Находим y"

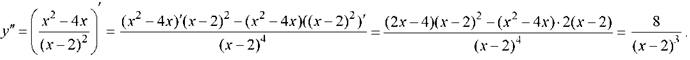
Так как у” >0 при х>2, то на интервале график во­гнутый; так как у"<0 при х<2, то на интервале график выпуклый.

8) Находим асимптоты графика:

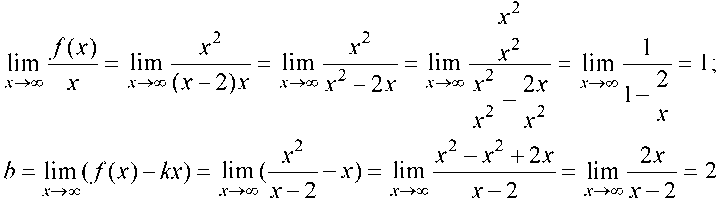
Таким образом, график имеет наклонную асимптоту у = х + 2. Строим график, который имеет в нашем случае вид (см. рис. 8.5).