1.Испытания и события. Виды случайных событий
Испытания и события. Выше событие названо случайным, если при осуществлении определенной совокупности условий S оно может либо произойти, либо не произойти. В дальнейшем, вместо того чтобы говорить «совокупность условий S осуществлена», будем говорить кратко: «произведено испытание». Таким образом, событие будет рассматриваться как результат испытания.
примеры испытаний и событий
Виды случайных событий. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.
События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое
2.Классическое определение вероятности
Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.
Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них красные, 3-синие и 1-белый. Очевидно, возможность вынуть наудачу из урны цветной (т.е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появление цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
(1)
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
Пример 1 Найти вероятность события А={появление не менее пяти очков при одном бросании игральной кости}.
Используем формулу (1). В нашем случае число возможных исходов n=6, а число, благоприятствующих этому событию исходов, m=2. То есть P(A)=2/6=1/3. Итак, вероятность появления не менее пяти очков при одном бросании игральной кости равна 0.33 или 1/3
3.сочетания перестановки размещения
Размещения.
Размещениями из 
элементов
по 
называются
соединения, которые можно образовать
из
элементов,
собирая в каждое соединение по
элементов,
при этом соединения могут отличаться
друг от друга как самими элементами,
так и порядком их расположения.
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие размещения:
ab, ac, ba, bc, ca, cb.
Число
всех возможных размещений, которые
можно образовать из
элементов
по
,
обозначается символом 
и
вычисляется по формуле:
,
(всего k множителей).
Пример: 
Перестановки.
Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.
Например, из 3 элементов (a,b,c) можно образовать следующие перестановки:
abc, bac, cab, acb, bca, cba.
Число
всех возможных перестановок, которые
можно образовать из n элементов,
обозначается символом 
(Произведение n первых целых чисел обозначается символом “n!” и читается “nфакториал”)
Пример: 
Сочетания.
Сочетаниями из n элементов по k называются соединения, которые можно образовать изn элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
Например, из 3 элементов (a,b,c) по 2 можно образовать следующие сочетания:
ab, ac, bc.
Число
всех возможных сочетаний, которые можно
образовать из n элементов
по k,
обозначается символом 
:
(В числителе и знаменателе по k множителей).
Пример: 
Полезные формулы:
Например: 
4
4.относительная частота
Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой
W (А) = m / n,
где m - число появлений события, n - общее число испытаний.
Сопоставляя определения вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.
5.геометрическая вероятность
Рассмотрим
какую-нибудь область |
в 
(на
прямой, на плоскости, в пространстве).
Предположим, что «мера»
(длина,
площадь, объем, соответственно) конечна.
Пусть случайный эксперимент состоит
в том, что мы наудачу
бросаем в эту область точку.
Термин «наудачу»
здесь означает, что вероятность
попадания точки в любую часть 
не
зависит от формы или расположения 
внутри
,
а зависит лишь от «меры»
области
(если
измеримо,
см. замечание 6).Определение 9.
Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можноизобразить точками некоторой области в так, что вероятность попадания точки в любую часть не зависит от формы или расположения внутри , а зависит лишь от меры области (и, следовательно, пропорциональна этой мере):
«Мерой» мы пока будем называть длину, площадь, объем и т.д.
Если для точки, брошенной в область , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области .
Пример 7.
Точка
наудачу бросается на отрезок [0,1].
Вероятность точке попасть в точку 
равна
нулю, так как мера множества, состоящего
из одной точки («длина точки»), есть 0.
Вместе с тем попадание в точку
не
является невозможным событием —
это один из элементарных исходов
эксперимента.
6.теорема сложения вероятностей
Теорема сложения вероятностей
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
Определение. Противоположными называются два несовместных события, образующие полную группу.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Определение. Событие А называется независимым от события В, вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
7.противоположные события
Противоположные события. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать
Теорема. Сумма вероятностей противоположных событий равна единице:
.
Доказательство базируется на том, что противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице (см. Теорему о полной группе событий).
З а м е ч а н и е 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы
p + q = l
З а м е ч а н и е 2. При решении задач на отыскание вероятности события А часто выгодно сначала вычислить вероятность противоположного события, а затем найти искомую вероятность по формуле
.
8.условная ,полная вероятность
Условная вероятность Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
Пусть 
—
фиксированное вероятностное пространство.
Пусть 
-
два случайных события, причём P(B)>0.
Тогда условной вероятностью события A при
условии события B называется
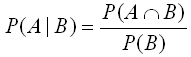
9.теорема умножения вероятностей
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Также можно записать:
Доказательство этой теоремы непосредственно вытекает из определения условной вероятности.
Если события независимые, то , и теорема умножения вероятностей принимает вид:
В случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились.
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.
Если в результате испытания может появиться п событий, независимых в совокупности, то вероятность появления хотя бы одного из них равна
Здесь событие А обозначает наступление хотя бы одного из событий Ai, а qi – вероятность противоположных событий .
Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.
Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.
Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.
Всего в колоде 13 червонных и 13 бубновых карт.
При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна , при вытаскивании второй карты - , третьей - , четвертой - .
Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна .
Тогда
Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей? Вероятность выпадения 6 очков при одном броске кости равна . Вероятность того, что не выпадет 6 очков - . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна .
Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна .
Пример. В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятности хотя бы одного выстрела, двух выстрелов, двух осечек.
Вероятность выстрела при первом нажатии на курок (событие А) равна , вероятность осечки - Вероятность выстрела при втором нажатии на курок зависит от результата первого нажатия.
Так если в первом случае произошел выстрел, то в барабане осталось только 3 патрона, причем они распределены по 5 гнездам, т.к. при втором нажатии на курок напротив ствола не может оказаться гнездо, в котором был патрон при первом нажатии на курок.
Условная вероятность выстрела при второй попытке - если в первый раз был выстрел, - если в первый раз произошла осечка.
Условная вероятность осечки во второй раз - , если в первый раз произошел выстрел, - если в первый раз была осечка.
Рассмотрим вероятности того, что во втором случае произойдет выстрел (событие В) или произойдет осечка (событие ) при условии, что в первом случае произошел выстрел (событие А) или осечка (событие ).
- два выстрела подряд
- первая осечка, второй выстрел
- первый выстрел, вторая осечка
- две осечки подряд
Эти четыре случая образуют полную группу событий (сумма их вероятностей равна единице)
Анализируя полученные результаты, видим, что вероятность хотя бы одного выстрела равна сумме
Теперь рассмотрим другой случай. Предположим, что после первого нажатия на курок барабан раскрутили и опять нажали на курок.
Вероятности первого выстрела и первой осечки не изменились - , Условные вероятности второго выстрела и осечки вычисляются из условия, что напротив ствола может оказаться то же гнездо, что и в первый раз.
Условная вероятность выстрела при второй попытке - если в первый раз был выстрел, - если в первый раз произошла осечка.
Условная вероятность осечки во второй раз - , если в первый раз произошел выстрел, - если была осечка.
Тогда:
- два выстрела подряд
- первая осечка, второй выстрел
- первый выстрел, вторая осечка
- две осечки подряд
В этом случае вероятность того, что произойдет хотя бы один выстрел, равна
10.независимость событий