Гистограмма

Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).

На рис. 6.2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.

Все население	В том числе в возрасте
	до 10	10-20	20-30	30-40	40-50	50-60	60-70	70 и старше	Всего
Численность населения	12,1	15,7	13,6	16,1	15,3	10,1	9,8	7,3	100,0

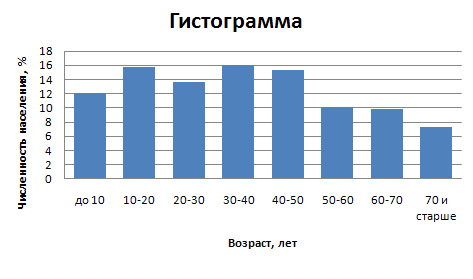
Рис. 6.2. Распределение населения России по возрастным группам

Условие: Приводится распределение 30 работников фирмы по размеру месячной заработной платы

Размер заработной платы руб. в месяц	Численность работников чел.
до 5000	4
5000 — 7000	12
7000 — 10000	8
10000 — 15000	6
Итого:	30

Задача: Изобразить интервальный вариационный ряд графически в виде гистограммы и кумуляты. Решение:

1. Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.

2. Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда. Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников.

3. Построим гистограмму:

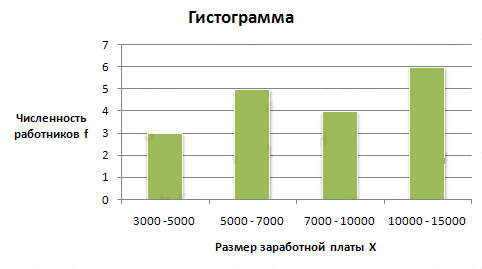
Для построения кумуляты необходимо рассчитать накопленные частоты (частости). Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше,чем рассматриваемое.

30.точечные распределения параметров распределения

Тема. Точечные оценки параметров распределения

8.1 Определения и основные свойства точечных оценок

Задача оценивания параметров распределения генеральной – одна из основных задач математической статистики. На содержательном уровне задача оценивания параметров распределения формулируется так: располагая выборкой реализаций случайной величины Х, необходимо получить оценку   неизвестного параметра генеральной совокупности а и ее статистические свойства.

Оценивание параметров распределения осуществляется в два этапа. На первом этапе, на основании выборки х1, х2, ... , ,хn ,строится статистика

,

значение которой при данной выборке х1, х2, ... , ,хn принимают за приближенное значение оцениваемого параметра а :

а .

Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку   называют точечной.

Для получения точечной оценки существует много статистик, которые могут быть использованы в качестве оценок. Поэтому второй этап оценивания состоит в выборе наилучшей оценки, что требует введения критерия качества получаемых оценок. Задача усложняется тем, что ввиду малого объема выборки требуется статистический подход к качеству оценки

По опытным данным (выборке) путем построения гистограммы или с помощью других средств можно попытаться выбрать вероятностную модель (определить закон распределения генеральной совокупности). При этом выборочные данные позволяют уточнить детали вероятностной модели. Знание вероятностной модели дает возможность прогнозировать будущие события, что важно для принятия решений. В приложениях обычно задаются определенным типом закона распределения генеральной совокупности (плотностью распределения)

f = f(x; a1, a2, ..., am)

и по данным случайной выборки х1, х2, ..., хn оценивают неизвестные параметры a1, a2, ..., am . Чаще всего параметрами являются генеральное среднее и дисперсия, а качестве оценки тогда используют выборочные характеристики: выборочное среднее и выборочную дисперсию.

Рассмотрим следующую задачу. Пусть имеется случайная величина Х и нам известен ее закон распределения f = f(x, a), который содержит один неизвестный параметр а. Требуется на основании выборочных данных х1, х2, ..., хn найти подходящую оценку параметра а. Для решения этой задачи построим следующую математическую модель. Пусть Х1, Х2, ..., Хn – независимые случайные величины, которые принимают соответствующие выборочные значения (для данной выборки значения х1, х2, ..., хn) и пусть случайная величина   получена на основе случайных величин Х1, Х2, ..., Хn, то есть   Будем считать, как и ранее, что случайные величины Х1, Х2, ..., Хn имеют один и тот же закон распределения с плотностью распределения величины Х (генеральной совокупности)f(x). Тогда   является случайной величиной, закон распределения которой зависит от n и от f(x). Для того чтобы оценка   имела практическую ценность она должна обладать следующими свойствами.

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

В противном случае оценка называется смещенной и допускает систематическую ошибку. Так, рассмотренное ранее среднее выборочное   является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия   - является смещенной оценкой генеральной дисперсии.

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

Это условие будет выполняться, если

и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

Такая оценка называется эффективной.

Заключение. При обработке экспериментальных данных необходимо руководствоваться сформулированными свойствами оценок.

В качестве примера покажем, что рассмотренные ранее оценки: выборочное среднее   и выборочная дисперсия  , будучи несмещенными, являются и состоятельными оценками. Действительно, так как согласно теореме Чебышева

то выборочное среднее  является состоятельной оценкой.

Для того чтобы доказать, что выборочная дисперсия   является состоятельной оценкой, покажем вначале, что смещенная оценка   - состоятельная оценка. С этой целью запишем:

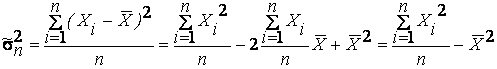 (8.1)

При n ® ¥ по вероятности случайная величина   стремится к М(Х2), а выборочное среднее   – к среднему генеральному mx. Тогда из соотношения (1) следует, что по вероятности   стремится при n ® ¥ к величине М(Х2)-mx2=D(X)=s2, которая является генеральной дисперсией. Тем самым доказана состоятельность оценки  . Если теперь рассмотреть несмещенную оценку генеральной дисперсии   то поскольку множитель   стремится к единице при n ® ¥, а   стремится по вероятности к  , то и оценка   стремится по вероятности к  , что доказывает состоятельность оценки  .

Замечание. Для простоты изложения формулы оценок математического ожидания и дисперсии, которые были использованы при доказательстве свойств оценок, были построены с использованием статистического ряда. Если данные выборки представлено в виде интервального вариационного ряда, то для вычисления соответствующих выборочных числовых характеристик используют следующие формулы.

1.Выборочное взвешенное среднее :

.

2. Выборочная взвешенная дисперсия :

,

которая является смещенной оценкой и несмещенная оценка

.

Здесь п – объем выборки, т – число разных вариант, nj – частоты вариант (п1+п2+…+пт=п).

8.2 Метод моментов

Метод моментов оценивания параметров распределения генеральной совокупности состоит в том, на основании выборки х1, х2, ..., хn вычисляются выборочные моменты (начальные или центральные). Полученные значения приравниваются соответствующим теоретическим моментам. Количество моментов должно ровняться числу оцениваемых параметров. Затем решают полученную систему уравнений относительно этих параметров.

Рассмотрим случай, когда метод моментов используется для нахождения оценки одного параметра. Положим, что плотность распределения f(x;a) случайной величины Х зависит только от одного параметраа, и необходимо найти оценку параметра а. Для нахождения оценки одного параметра достаточно иметь одно уравнение относительно этого параметра, используя, например, на основании выборки х1, х2, ... , ,хnпервый начальный момент

.

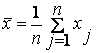Приравняем его значение первому теоретическому моменту

= ,

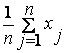рассматривая правую часть равенства как функцию от а. Решая это уравнение относительно неизвестного параметра а, получаем точечную оценку  , которая теперь является функцией от вариант выборки, то есть

.

Пример. Пусть Х – непрерывная случайная величина подчинена показательному (экспоненциальному) закону, плотность распределения которого зависит от одного неизвестного параметра  :

, х 0.

Используя полученные экспериментальные данные х1, х2, ... , хn, получить оценку параметра  .

Решение. На основании выборки х1, х2, ... , хn находим первый выборочный момент и приравниваем его первому моменту случайной величины Х, подчиненной показательному закону:

=  = .

Отсюда получаем оценку параметра  :

.▄

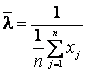Если функция плотности распределения случайной величины Х зависит от двух параметров, например  , то для отыскания оценок параметров   необходимо иметь уже два уравнения относительно этих параметров. Для этого можно воспользоваться, например, первым начальным моментом (математическим ожиданием) и вторым центральным (дисперсией).

Примеры.

1. По выборке х1, х2, ... , хп методом моментов найти точечные оценки параметров mx и   нормального распределения:

.

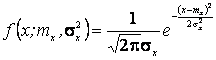Решение. Так как первый начальный момент нормального распределения равен параметру тх., а второй центральный момент равен параметру  ,

то

,  .

2. По выборке х1, х2, ... , хп методом моментов найти точечные оценки параметров а1, а2 равномерного распределения на интервале [а1, а2]:

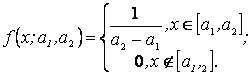
Решение. Используя выборку х1, х2, ... , хп, находим выборочные первый начальный и второй центральные моменты:

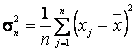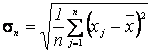, ,( ) (8.2)

Для равномерного распределения имеем теоретические моменты

,  .

Прировняем теоретические моменты выборочным и получаем систему двух уравнений с двумя неизвестными для нахождения оценок параметров а1, а2:

Решая эту систему, получаем в окончательном виде

,  ,

где величины  ,  определены соотношениями (2).