Билет 3. Позиционные системы счисления: их свойства, сравнительный анализ.

Определение. С.с позиционная, если количественный эквивалент каждой цифры в записи числа зависит не только от ее вида, но и от места в записи числа. Примером может послужить 10 с.с. Свойства позиционных систем счисления. 1) Мощность алфавита равна основанию IAI=s 2) Максимальная цифра в системе счисления равна 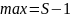3) Любое число в позиционной с.с. можно представить в виде полинома:

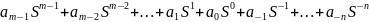
Система счисления

Непозиционная

Позиционная

Весомозначная

Невесомозначная

Без основания

С основанием

Целое

Дробное

Натуральное

Симметричное

Отрицательное

Положительное

Билет №4. Проблема выбора способов представления чисел в эвм.

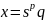
Формы представления чисел в ЭВМ 1) С фиксированной точкой (нормальная форма) а) перед старшим разрядом б) после младшего разряда преимущества: - использует меньшее количество оборудования для предоставления разряда числа - большая производительность - использование масштабов 2) С плавающей точкой – характеристика числа q - мантисса числа s – основание системы счисления p – порядок (положительное или отрицательное число) Пример. 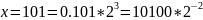Важнейшим условием при представлении числа в форме с плавающей запятой является условие нормализации // Условие нормализации Мантисса, удовлетворяющая данному условию называется нормализованной, а процесс приведения мантиссы в данное условие называется процессом нормализации мантиссы. Проблемы представления чисел в ЭВМ заключаются в следующем: 1) Неравномерное распределение чисел с плавающей запятой 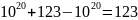На компьютере 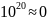2) Несоблюдение законов алгебры Пусть у нас есть верное математически тождество 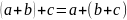Сначала выполняется действие в скобка, затем сложение скобок с полученным результатом в скобках, при сложении этих чисел с плавающей точкой верного тождества не получиться. Пусть основание равно 2.

Мантисса/Порядок	0	1	2	3
100	1/2	1	2	4
101	5/8	5/4	5/2	5
110	3/4	3/2	3	6
111	7/8	7/4	7/2	7

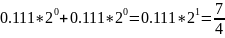
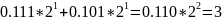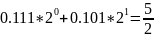
теперь с другой стороны 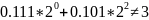3) Вычисление близких друг к другу величин получается с погрешностью

Билет №5. Преобразование чисел из одной позиционной системы счисления в другую Метод делении/умножения Xs=Xr(найти эквивалентную систему с основанием r) 1) Целая часть числа (деление) -Xs/r, остаток запоминается - Требуется проверить равно ли 0 частное, если нет, то Xs:=частное, переходим к предыдущему пункту, в противном случае переходим к следующему пункту - Запись результата: начиная со старшего разряда результата выписываем все заполненные остатки в порядке, обратном их очереди 2) Дробная часть числа (умножение) -Xs*r, целая часть результата запоминается -Требуется проверить равна ли нулю дробная часть, или достигнута ли заданная точность. Ежели нет, то Xs:=дробная часть, перейти к предыдущему пункту, в противном случае перейти к следующему пункту -Запись результата, начиная со старшего разряда выписываются все сохраненные целые части в порядке их получения. Преобразование чисел с основанием 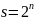-Преобразование двоичного числа в с.с. с 1) Разбиваем число на группы из n разрядов вправо и влево от запятой. 2) Каждая группа двоичных n разрядов заменяется эквивалентной цифрой из с.с Замечание. Если левые и правые крайние группы состоят менее чем из n разрядов, то они дополняются нулями слева и справа соответственно. -Преобразование из с.с. в двоичную с.с. 1) Каждая цифра в исходном числе заменяется двоичным числом из n разрядов Двоично-десятичные системы счисления Каждая десятичная цифра представляется четырехразрядным двоичным числом. Метод Рутисхаузера. 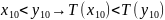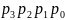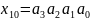Требования: 1) Единственность Каждой десятичной цифре должно соответствовать свое уникальное двоичное четырехразрядное число(тетрада) 2) Монотонность 3) Четность Если х10 четная, то Т(х10) тоже четная, также и с нечетностью 4) Весомозначность Существуют , такие, что если , то 5) Дополнительность Eсли х10+у10=9, то тетрады соответствующие им дополняют друг друга. 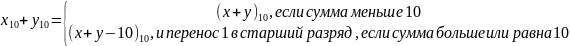Но выполняются не все требования 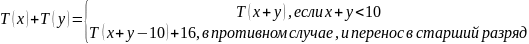Код прямого замещения (код 8421) 0-0000 1-0001 ………… 9-1001 При сложении чисел кода прямого замещения выполняются правила двоичного сложения. Результирующие тетрады корректируются прибавлением 0110 в следующих случаях: - если получена неправильная тетрада - если из рассматриваемо1й тетрады произошел перенос единицы в старшую тетраду. Код с избытком 3 Каждая десятичная цифра, представленная в двоичном эквиваленте увеличивается на 3 0-0011 1-0100 ………… 9-1100 В данном коде происходит коррекция на 3 (0011) в тех же случаях, что и в коде 8421. Билет №6. Кодирование отрицательных чисел в ЭВМ Для определения знака числа в двоичном коде используются 0 и 1. Нулем кодируется знак "+", Единицей кодируется знак "-". Для представления положительных и отрицательных чисел в вычислительной технике используются ПРЯМОЙ, ОБРАТНЫЙ и ДОПОЛНИТЕЛЬНЫЙ коды. Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково  -  двоичными кодами с цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например: 

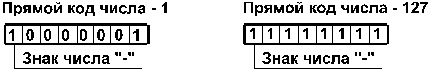
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа. В общем виде для любой системы счисления это выглядит следующим образом: Прямой код: ,где s-основание с.с. 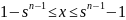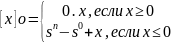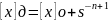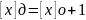Диапазон представления для прямого кода, при сетки из n разрядов: //дробные числа //целые числа Дополнительный код: // дробные числа //целые числа Обратный код: // дробные числа //целые числа Для положительных чисел обратный, дополнительный и прямые коды совпадают, а для отрицательных имеет место следующее соотношение: // дробные числа // целые числа Диапазон размещения чисел для дополнительного и обратного кода //дробные числа //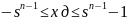целые числа 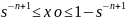//дробные числа //целые числа