50. Способ последовательного дифференцирования.

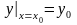
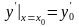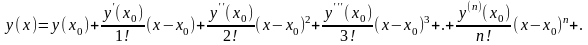
Если ур-ние имеет вид Имеем раз-ние в ряд Тейлора 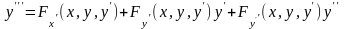Исследуем сходимость полученного ряда, в который подставляем начальные условия.Ряды можно использовать для решения алгебраических уравнений. Вида 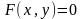. Решение таких уравнений осущ методом неопред коэф и послед дифференцированием.

51. Периодические функции. Тригонометрические. Определение коэффициентов методом Эйлера –Фурье.

Периодическая функция с периодом 2П, удовлетворяющая на интервале (-П, П) условиям Дирихле, может быть представлена рядом Фурье:

коэффициенты которого находятся по формулам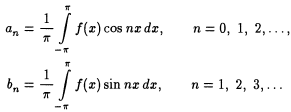

В точках непрерывности функции f(x) ряд Фурье сходится к f( ), а в точках разрыва — к . Разложение в ряд Фурье периодической функции f(x) с периодом 2l имеет вид где

53 Ортогональные системы функций. Ряд Фурье по произвольной ортогональной системе функций.Определение 1. Бесконечная система функций f₁(x), f₂(x)..f_n(x) (1) называется ортогональной на отрезке [а, b], если при любых n≠k выполняется равенство 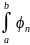(x)ϕ_k(x)dx=0(2) При этом предполагается, что dx≠0 Пусть функция ϕ(x)_, определенная на отрезке [а, b], такова, что она представляется рядом по функциям ортогональной системы (1), который сходится к данной функции на [а, b]: f(x)=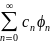 (x) (6). Определим коэффициенты с_п. Допустим, что ряд, полученный после умножения ряда (6) на любую ϕ_k(х), допускает почленное интегрирование. Умножим обе части равенства (6) на ϕ_k(x) и проинтегрируем в пределах от а до b. Учитывая равенства (2), получим 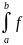(x)ϕ_k(x)dx=c_k 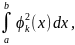откуда 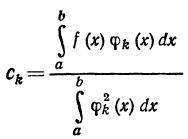(7) Коэффициенты с_к , вычисленные по формулам (7), называются⁵ ко­эффициентами Фурье функции f (х) по системе ортогональных функций (1). Ряд (6) называется рядом Фурье по системе функ­ций (1).

54. Условия Дирихле. Достаточное условие представления функции в ряд Фурье.Функция f(x) определенна и непрерывна в некоторой области значений х, называется не убывающей(не возрастающей) если из условия х₂>x₁ ; f(x₂)≥f(x₁) -не убывающая f(x₂)≤f(x₁)- не возрастающая Функция f(x) называется кусочно монотонной на отрезке [a;b] если этот отрезок можно разбить на конечное числом точек х₁, х₂, х₃….. х_n-1 на интервалы [a;x₁);(x₁;x₂);(x₂,x₃)…....(x_n-1,b] так что на каждом из интервалов функция монотонна, тоесть либо не убывает, либо не возрастает ,из этого следует что если функция f(x) кусочно монотонная и ограничена на отрезки [a;b] то она может иметь точки разрыва 1 рода. х=с 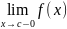=f(c-0) =f(c+0);f(c-0) f(c+0).Т.Дирихле.Если функция f(x) с периодом 2π кусочно монотонная и ограниченая на замкнутом промежутке х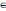 [-π;π], то ряд Фурье построеный на этой функции сходится во всех точках сумма полученного ряда S(х) равна значению f(x) в точках непрерывности этой функции, в точках разрыва функции f(x) сумма ряда равняется среднему арифмитическому приделу функции f(x) справа и слева.S(c)={f(c-0)+f(c+0)}/2.Условия данной теоремы называются условиями Дирикхле.

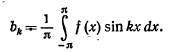
55.Разложение четных/нечетных функций в ряд Фурье.

Из определения четной и нечетной функции следует, что если ψ(х)-четная функция, то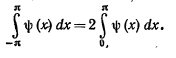 Действительно

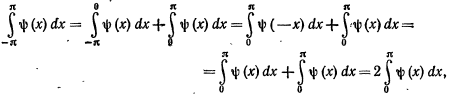Так как по определению четной функции ψ(-х)= ψ(х).

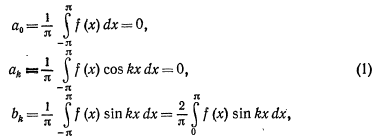Аналогично можно доказать, что если φ(х)-нечетная функция то Если в ряд Фурье разлагается нечетная функция f(x), то произведение f(x)cos(kx) есть функция также нечетная, а f(x)sin(kx)-четная; следовательно Тоесть ряд Фурье нечетной функции содержит “только синусы”

Если в ряд Фурье разлагается четная функция, то произведение f(x)sin(kx) есть функция нечетная, а f(x)cos(kx)-четная , следовательно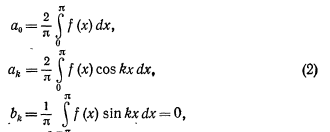

Тоесть ряд Фурье четной функции содержит “только косинусы” Полученные формулы позволяют упрощать вычисления при разыскании коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной. Очевидно, что не всякая периодическая функция является четной или нечетной.