45. Дифференцирование степенных рядов

Теорема 1. Если степенной ряд s(x) = a₀ + a₁x + a₂x² + a₃x³...+ а_nхⁿ +...(1) имеет интервал сходимости (— R_y R), то ряд ϕ(x) = a₁+ 2а₂х + 3а₃х² +... + nа_n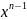 + ...,(2) полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимости (—R, R) при этом ϕ (х) = s' (х), если |x|<R_, т. е. внутри интервала сходимости производная от суммы сте­пенного ряда (1) равна сумме ряда, полученного почленным диф­ференцированием ряда(1) Доказательство.Докажем, что ряд (2) мажорируем на любом отрезке [—р, р]„ целиком лежащем внутри интервала сходимости.Возьмем точку Ɛ такую, что р < Ɛ < R (рис. 1). В этой точке ряд (1) сходится, следовательно, 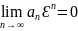, поэтому можно указать такое постоянное число М, что 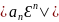<M(n=1,2,..) Если |х|<р, тo 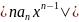≤ |=n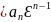 || |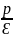^n-1<n q^n-1 где q=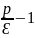 Таким образом, члены ряда (2) при |x|≤р по абсолютной величине меньше членов числового положительного ряда с посто­янными членами (1+2q+3q²+..+nq^n-1+..) Но последний ряд сходится, в чем можно убедиться, применяя признак Даламбера: =q<1 Следовательно, ряд (2) мажорируем на отрезке [—р, р], и на Основании теоремы его сумма есть производная от суммы данного ряда на отрезке [—р, р], т. е. ϕ(x)=s`(x) Так как всякую внутреннюю точку интервала (—R, R) можно заключить в некоторый отрезок [—р, р], то отсюда следует, что ряд (2) сходится в любой внутренней точке интервала (—R, R). Докажем, что вне интервала (—R, R) ряд (2) расходится. Допустим, что ряд (2) сходится при х₁ > R. Интегрируя его почленно в интервале (0, х₂), где R <x₂ < x₁ мы получили бы, что ряд (1) сходится в точке х₂ а это противоречит условиям теоремы. Таким образом, интервал (—R, R) есть интервал схо­димости ряда (2). Теорема полностью доказана. Ряд (2) снова можно почленно дифференцировать и продол­жать так сколь угодно раз. Таким образом, получаем вывод:Теорема 2. Если степенной ряд сходится в интервале (—R_, R), то его сумма представляет собой функцию, имеющую внутри интервала сходимости производные любого порядка, каж­дая из которых есть сумма ряда, получающегося в результате почленного дифференцирования данного ряда соответствующее число раз; при этом интервал сходимости каждого ряда, полу­чившегося в результате дифференцирования, есть тот же интер­вал (— R, R).

46. Ряды по степеням (x–a).К степенным рядам относятся: (1)Где есть постоянные коэффициенты степенного ряда.Находим область сходимости: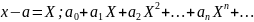 ; Для нахождения радиуса сходимости: ; ;

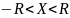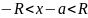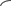
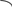
О 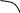тсюда:

a - R

a

a+R

|X| > R

47. Ряды Тейлора и Маклорена.Пусть задана фун. y=f(x) которая имеет все производные до (n+1) включительно в какой-то точки x₀ принадлежащей некоторому промежутку Найдем такой многочлен y=P_n(x) значения которого в точке x₀ равны значениям этой функции и причем производные любого порядка тоже равняются.P_n(x₀) =f(x₀); P_n ^/ (x₀) =f ^/ (x₀);…….. P_n⁽ⁿ⁾(x₀) =f⁽ⁿ⁾(x₀) (1) P_n(x)=C₀+C₁(x-x₀)+C₂(x-x₀)²………C_n(x-x₀)ⁿ ;P_n ^/ (x)= C₁+2C₂(x-x₀)………nC_n(x-x₀)^n-1………….

P_n⁽ⁿ⁾(x)= n!C_n ;С₀=f(x₀); 1*С₁=f ^/ (x₀); 1*2С₂=f ^// (x₀);…………… n!С_n=f ⁽ⁿ⁾ (x₀);P_n(x)=f(x₀)+( f ^/(x₀)(x-x₀) ) / (1!) +( f ^// (x₀)(x-x₀)² ) / (2!)+……..+( f⁽ⁿ⁾(x₀)(x-x₀)ⁿ ) / (n!) ….(2)

f(x)=P_n(x)+R_n(x) Можем показать что остаток R_n(x) при х→х₀ есть величина бесконечно малая большая чем (х-х₀)ⁿ ;R_n(x)=0*((х-х₀)ⁿ O малое.(3) Учитывая (2) и (3) получим f(x)= f(x₀)+( f ^/(x₀)(x-x₀) ) / (1!) +( f ^// (x₀)(x-x₀)² ) / (2!)+….+( f⁽ⁿ⁾(x₀)(x-x₀)ⁿ ) / (n!)+0*((х-х₀)ⁿ)… (4);(4)- формула Тейлора для фун. f(x) в окрестности точки х₀ с дополнением(остаточным членом в форме Пеано) Полученная формула является обобщенной формулой для приращения функции f(x)= f(x₀)+( f ^/(x₀)(x-x₀) ) +0*((х-х₀)ⁿ) (из (4) следует что n=1) Данное представление для f(x) в окрестности х₀ является единственным .Пусть в окрестности х₀ фун. f(x) имеет два представления f(x)=A₀+A₁(x-x₀)+A₂(x-x₀)²+……A_n(x-x₀)ⁿ +0*((х-х₀)ⁿ)………..(5);f(x)=A₀ ^/+A₁ ^/ (x-x₀)+A₂ ^/ (x-x₀)²+……A_n ^/ (x-x₀)ⁿ +0*((х-х₀)ⁿ)……….(6);приравняем (5) и (6) и устремим х→х_{0 ;}(5)=(6)………………..(7);А₀=А₀ ^/…….А_n=А_n ^/ х-х₀=∆х f(x)-f(x₀)= ∆y;∆y= (f ^/(x₀) ∆х ) / (1!)+ (f ^// (x₀) ∆х ² ) / (2!)+….+( f⁽ⁿ⁾(x₀) ∆х ⁿ ) / (n!)+0*(∆х ⁿ)…….(8) Соотношение (8) является обобщенной формулой приращения функции ∆f(x₀)=f ^/ (x₀) ∆х+0*(∆х ⁿ) Рассмотрим (4) с остаточным членом в форме Лангранжа f(x)= f(x₀)+( f ^/(x₀)(x-x₀) ) / (1!) +( f ^// (x₀)(x-x₀)² ) / (2!)+….+( f⁽ⁿ⁾(x₀)(x-x₀)ⁿ ) / (n!)+R_n(x)..(9);R_n(x)= {(x-x₀)ⁿ⁺¹ / ((n+1)!)}* fⁿ⁺¹(x₀+Q(x-x₀)) ……(10);0<Q(x-x₀)<1. Если f(x) имеет производные всех порядков в окрестности точки х₀ то в формуле Тейлора (9) число n можно брать сколь угодно большое, тогда ряд (9) сходится и фун. f(x) если 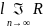_n(x)=0 Если в формулах (9) и (10) положить х₀=0 то данные формулы примут вид: f(x)= f(0)+(f ^/(0)x) / (1!) +( f ^// (0)x² / (2!)+….+( f⁽ⁿ⁾(0)xⁿ / (n!)+R_n(x)…….(11);R_n(x)= {(x)ⁿ⁺¹ / ((n+1)!)}* fⁿ⁺1(Q(x));0<Q<1;(11)-Ряд Маклорена.Существует такое х₀ и R что в интервале (х₀-R; x₀+R ) что данная функция разложиться в ряд Тейлора и Маклорена. Если для какой ни будь функции формально записан ряд Тейлора, то чтобы доказать что ряд представляет данную функцию необходимо доказать что остаточный член=0 либо иным способом доказать что написанный ряд сходится к данной функции

48. Разложение элементарных функций в ряд Маклорена.

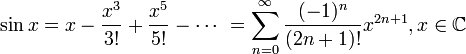
49. Интегрирование дифур с помощью рядов.1 способ:В исходный дифур. Подставляем y в виде степенного ряда.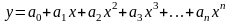 Приравнивая коэф-ты при одинаковых степенях х получаем систему уравнений для опр-я коэф-в.

2 способ(ур-е вида 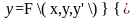; ; Продолжая этот процесс можно получить все слагаемые