14. Основные свойства двойных интегралов.

1. Двойной интеграл по области D = площади этой области.

2. Если область G содержится в D, а ф-ция ограничена и интегрируема в D, то она интегрируема и в G.

3. Аддитивное св-во. Если область D при помощи кривой L разбивают на 2 области D 1 и D 2, не имеющих общих внутренних точек, то:

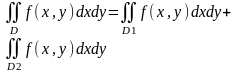
4. Константы выносятся за знак интеграла, а сумму в ф-ции можно представить в виде суммы интегралов:

5. Если ф-ции f и g интегрируемы в D, то их произведение также интегрируемо в D. Если g(x,y)  0 то и f/g интегрируема в D.

6. Если f(x,y) и g(x,y) интегрируемы в D и всюду в этой области f(x,y) <= g(x,y), то:

В частности: g(x,y) >=0 то и

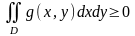
7. Оценка абсолютной величины интеграла: если f(x,y) интегрируема в D, то и |f(x,y)| интегрир. в D причем

обратное утверждение неверно, из интегрируемости |f| не следует интегрируемость f.

16. повторные интегралы Правильная область.Опр1. Пусть в обрасти G лежащей в плоскостях Оу яв-ся правильной в направлении оси Оу это значит ,

что всякая прямая и проходящая через эту точку пересекает границу этой области в 2х точках. х є [a,b] (x) ≥ (x ) Неправильная область аналогичным образом определим правильную опласть в направлении ося Ох. Если область правильная в Ох о Оу, то пространство правильное.

Всякую область всегда можно представить в виде суммы правильных областей в виде по оси Ох либо по Оу. I(по области G) (1) (интегрируется по у считаем что х Константа)I(x)=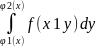 ; I(по G)= 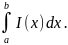Свойства: 1) если правильную область G разбить на 2 области и прямой то интеграл (1) равен сумме таких же интегралов по областям G1 и G2. 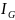= + (2)Док-ва Проведем прямую которая пересечет плоскость в точке. С формулой 2. (по области G) = (по свойству одномерных интегралов) С= Следствие1Если область Gразбить прямыми параллельными осями координат на любое число про областей G1иG2, Gn будет равняться повторный интеграл семе интегралов по соответствующ. Области 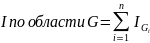(4) по области G= (4) Свойство2

повторн интеграл оценка двукратного интеграла пусть m и M соответственно наименьшим и наибольшим и наибольшем значением функции f от f(x,y) и S это площадь области G.Тогда справедлива след оценка m по области G (5) учитывая формулы 1 и 2 след:I= 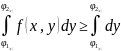=m Площадь области G G G

16. Замена переменных в двойном интеграле. Пусть непрерыв­но дифференцируемые функции х = х{и₎ v),

— якобиан отображения D_x на D.

у = у{и₎ и) взаимно одно­значно отображают область D_x плоскости и₎ v на область D плоско­сти х₎ у₎ а функция f{x₎ у) непрерывна в D. Тогда

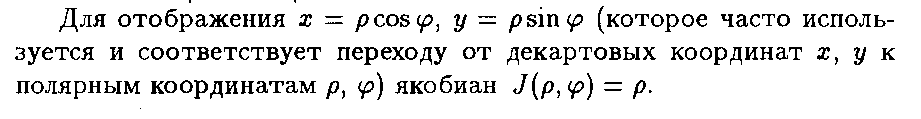
17. Вычисление криволинейного интеграла в полярной и обобщенной полярной системе координат

Полярная система координат :Функцию F(x,y) выражаем в полярной системе координат:X=ρcosφ,Y=ρsinφ.Якобиан перехода – ρ, т.е. интеграл, из получившихся в результате перехода функций мы умножаем на ρ. (1).Берем интеграл от полученной функции по dρ и dφ(предварительно расставив пределы интегрирования с помощью графика функции).Обобщенная полярная система координат:Функцию F(x;y) выражаем в обобщенной полярной системе координат:X=a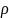 cosφ,Y=bρsinφ.Якобиан перехода – abρ (определение аналогично с 1).Дальнейшие действия аналогичны с теми, что производятся при вычислении в полярной системе координат.

18. Вычисление двойного интеграла.Пусть у1(х), у2(х) непрерывны на отрезке [a, b], у1(х)<= у2(х) на всем отрезке.D={x,y}: a<=x<=b; y1(x)<=y<=y2(x)

Отрезок [a,b] – проекция Д на ось ох. Для такой области людбая прямая, параллельная оу и проходящая через внутреннюю точку области Д пересекает границу области не более чем в 2 точках. Такая область наз. правильной в направлении оси оу. Если фция f(x,y) задана на Д и при каждом х  [a,b] непрерывна на у , на отрезке, [y1(x),y2(x)], то фц-ия F(x) = 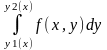, наз. интегралом, зависящим от параметра I, а интеграл : , наз повторным интегралом от ф-ции f(x,y) на области Д. Итак, повторный интеграл вычисляется путем последовательного вычисления обычных определенных интегралов сначала по одной., а затем по другой переменной.

19. Определение тройного интеграла.Р ассмотрим тело, занимающее пространственную область Q. И предположим, что плотность распределения массы в этом теле является непрерывной функцией координат точек тела:

δ = δ (х, у, z). Разобьем тело произвольным образом на n частей; объемы этих частей обозначим: ∆v₁, ∆v₂, …, ∆v_n. Выберем затем в каждой части по произвольной точке P_i(x_i, y_i, z_i).Полагая, что в каждой частичной области плотность постоянна и равна ее значению в точке P_i, мы получим приближенное выражение для массы всего тела в виде суммы (*).

_n

M_n = ∑ δ (х_i, у_i, z_i) ∆v_i (*)

ⁱ⁼¹

_n

M = lim ∑ δ (х_i, у_i, z_i) ∆v_i = ∫∫∫ δ (х, у, z) dv

^{i=1 Q}

Cумма (*) называется n-й интегральной суммой, а ее предел – тройным интегралом от функции δ = δ (х, у, z) по пространственной области Q.

_n

∫∫∫ f (х, у, z) dv = lim ∑ f(x_i, y_i, z_i) ∆v_i

^{Q i=1}

Где f(x, y, z) – произвольная непрерывная в области Q функция.

20. Свойства трехкратного интеграла.Если область V разбить на две области V₁ и V₂ плоскостью || какой-либо из координатных плоскостей, то трехкратный интеграл (1)Равен сумме трехкратных интегралов по обл. V₁ и V₂.Следствие:При любом разбиении обл. V на конечное число обл. V₁, V₂, …, V_nПлоскостями || координатным плоскостям, то будем иметь:I_v=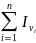 Теорема об оценке трехкратного интегралаПусть М и m соотв. Наибольшее и наименьшее знач-е ф-и в обл. V.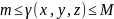 В этом случае справедливо:mV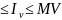 (2)Док-во:Запишем (1) ->

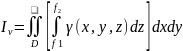(3)Учитывая огр. m и M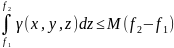 (4) Подставим,

Аналогично доказывается и левая часть док-ва (2)Теорема о среднем Трехкратный интеграл I_v от неприрыв. по замкнут обл. V равен произведению объема обл. на значение ф-и в нек-ой точке Р, принадлеж. V. (5)Док-во:Из (2) имеем По теореме (Больцана – Коши) Веерштрассе: Существует хотя бы одна точка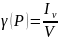 , P

21. Трехмерная область V, ограниченная замкнутой поверхностью S, называется правильной, если:любая прямая, параллельная оси Оz и проведенная через внутреннюю точку области, пересекает S в двух точках;вся область V проектируется на плоскость Оху в правильную двумерную область D;любая часть области V, отсеченная от нее плоскостью, параллельной какой-либо из координатных плоскостей, обладает свойствами 1 и 2. Назовем трехкратным интегралом от функции f(x, y, z) по области V выражение вида:                                      Св-ва:Если область V разбить на две области V1 и V2 плоскостью, параллельной какой-либо из координатных плоскостей, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V1 и V2. Если известны наименьшее m и наибольшее M значения непрерывной функции f(x;y;z), (x;y;z) U в области U, то тройной интеграл оценивается так:

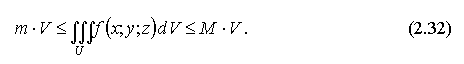
1. (о среднем значении для тройного интеграла):

2. где M_* – некая "средняя" точка области U, f(x; y; z) – непрерывна в U.ДоказательствоИспользуем свойство : 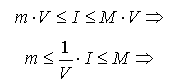  Число I/U – является промежуточным значением непрерывной функции f(x ;y; z), поэтому существует точка M_*, такая, что   в итоге  ,Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области: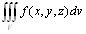 .     (9.3)Доказательство.Разобьем область V плоскостями, параллельными координатным плоскостям, на п правильных областей . Тогда из свойства 1 следует, что 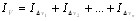        ,где 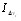- трехкратный интеграл от функции f(x,y,z) по области 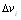.Используя формулу (9.2), предыдущее равенство можно переписать в виде:           .Из условия непрерывности функции f(x,y,z) следует, что предел интегральной суммы, стоящей в правой части этого равенства, существует и равен тройному интегралу . Тогда, переходя к пределу при 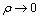, получим:                         IV = ,что и требовалось доказать. Замечание изменение порядка интегрирования не меняет значения трехкратного интеграла.Всякую область можно разбить на правильные подобласти

22. Вычисление тройного интеграла в цилиндрических и сферических координатах. Цилиндрические

Введем в пространстве цилиндрические координаты. Для этого на плоскости  используем полярные координаты, а третья координата произвольной точки  остается  . Учитывая связь полярных координат с декартовыми, получим выражение декартовых координат через цилиндрические:  . Тогда   и тройной интеграл в цилиндрических координатах вычисляется по формуле:  . Элемент объема в цилиндрической системе координат есть   . Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где ρ − длина радиуса-вектора точки M;φ − угол, образованный проекцией радиуса-вектора   на плоскость Oxy и осью Ox;θ − угол отклонения радиуса-вектора   от положительного направления оси Oz (рисунок 1). Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга. Сферические координаты точки связаны с ее декартовыми координатами соотношениями

Якобиан перехода от декартовых координат к сферическим имеет вид:

Раскладывая определитель по второму столбцу, получаем Соответственно, абсолютное значение якобиана равно Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:

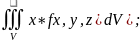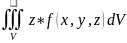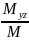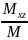23. Приложение тройного интеграла1) Объем ϕ(x,y,z)≡1;2) Масса ϕ(x,y,z)= , M= 3)Статический момент относительно координатных плоскойтей M_yz= M_xz= ;M_xy= ;4) Центр тяжести тела V с плотностью ϕ . X_c= , y_c= , z_c=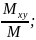 5) Момент инерции Y_xx=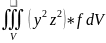

25. Сведение криволинейного интеграла первого рода к обыкновенному.Предположим, что на кривой (К) произвольно установлено направление (одно из двух возможных), так что положение точки М на кривой может быть определено Длиной дуги s= , отсчитываемой от начальной точки А. Тогда кривая (К) параметрически выразится уравнениями вида:x=x(s), y=y(s), (0≤ s ≤S) ,а функция f(x,y) заданная в точках кривой, сведется к сложной функции f(x(s), y(s)) от переменной s.Если через s_i(i=0, 1,……,n) обозначить значения дуги, отвечающие выбранным на дуге АВ точкам деления А_i , то очевидно σ_i= s_i+1 - s_i=∆s_i . Обозначив через _i значения s, определяющие точки М_i (причем очевидно, s_i ≤ _i ≤ s_i ), видим что интегральная сумма для криволинейного интеграла 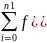_i)σ_i = 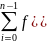_i), y( _i))∆s_i является в то же время интегральной суммой для обыкновенного определенного интеграла, так что сразу имеем: Причем существование одного из интегралов влечет за собой существование другого.

Интеграл, очевидно, существует, например в случае непрерывности функции f(M),что мы будем впредь предполагать Пусть теперь кривая (К) задана произвольными параметрическими уравнениями

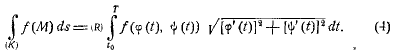Где функции φ и ψ непрерывны со своими производными и ; предположим, сверх того, что кратных точек на кривой нет. Тогда кривая заведомо спрямляема, и если возрастание дуги s= =s(t) отвечает возрастанию параметра t, то Заменяя переменную в интеграле (3) справа, получим Таким образом для вычисления криволинейного интеграла первого типа надлежит заменить в под интегральной функции переменные x и y выражениями координат через параметр, а множитель ds-дифференциалом дуги как функции параметра.В случае кривой заданным явным уравнением:y=y(x) (a ≤ x ≤ b);формула (4) примет вид