Физический маятник

Физическим маятником называется тело, закрепленное на оси, не проходящей через центр масс этого тела.

На маятник действует сила тяжести , и под действием этой силы маятник совершает колебания на рис.

При отклонении маятника на некоторый угол от положения равновесия возникает возвращающий момент силы тяжести, который стремится вернуть маятник в положение равновесия. Этот момент равен (в скалярном виде):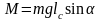 , где расстояние – плечо силы.Запишем основное уравнение динамики вращательного движения для маятника:

,где I – момент инерции тела;

– угловое ускорение тела; – момент внешних сил, действующих на тело.

Запишем уравнение в скалярном виде. Для этого спроецируем векторы момента сил и углового ускорения на произвольную ось, перпендикулярную плоскости колебаний маятника.Видно,что указанные векторы направлены в противоположные стороны, поэтому их проекции имеют разные знаки. Получаем:

.Рассмотрим небольшие колебания маятника, при которых . Для таких колебаний уравнение можно записать в виде:

.Разделив уравнение на момент инерции I и перенося все слагаемые в левую часть уравнения, запишем (с учетом того, что 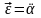): .Полученное уравнение совпадает с уравнением гармонического осциллятора. Собственная частота физического маятника: , период колебаний:

Решением уравнения будет являться выражение, описывающее зависимость от времени угла отклонения маятника от положения равновесия:

.Рассмотрим физический смысл собственной частоты в данном примере. Для получения выражения поступим таким же образом, что и при выводе выражения . Домножим и разделим возведённое в квадрат уравнение на угловое смещение  :

.Полученное выражение имеет тот же физический смысл, что и выражение для собственной частоты в случае пружинного маятника.

Математический маятник.

Математическим маятником называется точечная масса m, подвешенная на невесомой нерастяжимой нити на рис.

Математический маятник представляет собой частный случай физического маятника, вся масса которого сосредоточена в одной точке. На маятник действует сила тяжести ,и, следовательно, возникает возвращающий момент силы. Модуль момента с учетом малости колебаний составит

.Запишем основное уравнение динамики вращательного движения с учетом разнонаправленности векторов углового ускорения и момента силы тяжести :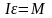 .Момент инерции I маятника равен моменту инерции материальной точки массы m, находящейся на расстоянии l от оси вращения:

.Учтем, что угловое ускорение и перепишем уравнение с использованием:

.Деля уравнение на ml² и перенося все слагаемые в левую часть, получим: , или .Видно, что полученное уравнение аналогично уравнению гармонических колебаний (1.13). Итак, математический маятник является (при небольших колебаниях) гар-моническим осциллятором, колеблющимся с собственной частотой: и периодом

,причем ни частота ни период не зависят от массы маятника. Решением уравнения будет являться уравнение вида с учетом того, что собственная частота определяется с помощью .Физический смысл собственной частоты математического маятника,как частного случая физического маятника, не изменился. Чтобы пояснить это, умножим и разделим квадрат уравнения на :

Полученное выражение совпадает по физическому смыслу с рассмотренным ранее выражением для собственной частоты пружинного и физического маятника.Между физическим и математическим маятником существует дополнительная связь. 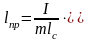Приравняем выражения и,описывающие периоды колебаний обоих маятников: Сократим на 2π и возведем в квадрат: Видно, что физический маятник, обладающий массой m, моментом инерции I и имеющий расстояние l_c от точки подвеса до центра масс, колеблется с тем же периодом, что и математический маятник длиной Длина l_пр называется приведенной длиной физического маятника.

Если в физическом маятнике продолжить линию, связывающую точку подвеса О и центр масс С, и на расстоянии l_пр от точки подвеса поставить точку О΄, то окажется, что физический маятник, подвешенный за эту точку, будет колебаться с той же частотой, как и будучи подвешенным за точку О на рис.

Точка О΄, называется центром качания физического маятника. Точка подвеса и центр качания обладают свойс-твом взаимности: если физический маятник подвесить за центр качания, то прежняя точка подвеса станет центром качания, и наоборот.