8.. Размерность и базис векторного пространства

 Векторное пространство   называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.

Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.

Размерность пространства   условимся обозначать через dim.

Например, размерность множества всех плоских векторов равна 2, размерность множества пространственных векторов равна 3.

Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.

Совокупность n линейно независимых векторов n- мерного векторного пространства   называется его базисом.

Теорема 5.1. Каждый вектор   линейного n- мерного пространства   можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

Доказательство. Пусть   - произвольный базис пространства   и  . Так как любые n+1 векторов пространства   линейно зависимы, то зависимы, в частности, и векторы  , т.е. существуют не равные одновременно нулю числа  , такие, что

.

При этом  , в противном случае хотя бы одно из чисел   было бы отлично от нуля, и вектора   были бы линейно зависимы. Следовательно,

.

Полагая  , будем иметь  .

Это представление   через   единственно. Доказывается от противного. Числа   называются координатами вектора   в базисе  .

Теорема 5.2. Если   - линейно независимые векторы пространства   и любой вектор   линейно выражается через  , то эти векторы образуют базис в  .

Доказательство. Векторы  , по условию, линейно независимы. Покажем, что в пространстве   нет более чем n линейно независимых векторов. Выберем произвольные   векторов из  :  . По условию, каждый из них можно линейно выразить через  :

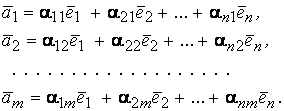
Рассмотрим матрицу:

.

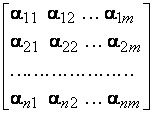Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то mстолбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы  . Итак, пространство   n – мерно и   - его базис.

 

9. Пусть в пространстве имеется два базиса: и .

Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 5.1, можно линейно выразить через векторы старого базиса:

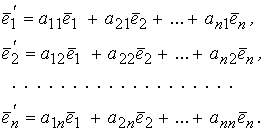(5.1)

Новые базисные векторы получаются из старых с помощью матрицы

При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица   называется матрицей перехода от базиса   к базису  .

Определитель матрицы   не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы  , были бы линейно зависимы.

Обратно, если  , то столбцы матрицы линейно независимы, и следовательно векторы  , получающиеся из базисных векторов   с помощью матрицы  , линейно независимы и значит образуют некоторый базис. Таким образом, матрицей перехода может служить любая квадратная матрица порядка n с отличным от нуля определителем.

Рассмотрим теперь, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть   в старом базисе и   - в новом. Подставляя в последнее равенство вместо   их выражение из (5.1), получим, что

        Таким образом, старые координаты вектора   получатся из новых его координат с помощью той же матрицы  , только коэффициенты соответствующих разложений образуют строки этой матрицы.