Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Осетинский государственный университет им. К. Хетагурова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Копия алгебра.doc

Скачиваний:

Добавлен:

26.09.2019

Размер:

873.47 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

6. Вектор – это направленный отрезок прямой.

То есть, в качестве вектора мы принимаем отрезок на плоскости или в пространстве, считая одну из его граничных точек началом, другую – концом.

Для обозначения векторов будем использовать строчные латинские буквы со стрелочкой над ними, например . Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как .

Определение.

Нулевой вектор – это любая точка плоскости или пространства.

Будем считать, что нулевому вектору можно придать любое направление на плоскости и в пространстве.

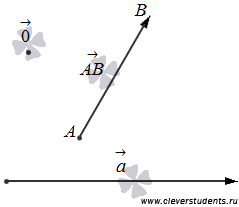
Определение.

Длина вектора - это неотрицательное число, равное длине отрезка АВ.

Длину вектора будем обозначать как .

Так как обозначение длины вектора в точности совпадает со знаком модуля, то можно услышать, что длину вектора называют модулем вектора. Все же рекомендуем использовать термин "длина вектора". Длина нулевого вектора равна нулю.

Определение.

Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Определение.

Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.

Нулевой вектор коллинеарен любому другому вектору.

Определение.

Два коллинеарных вектора и называют сонаправленными, если их направления совпадают и обозначают .

Определение.

Два коллинеарных вектора и называют противоположно направленными, если их направления противоположны и обозначают ).

Будем считать, что нулевой вектор сонаправлен с любым другим вектором.

Определение.

Два вектора называются равными, если они сонаправленные и их длины равны.

Определение.

Два вектора называются противоположными, если они противоположно направлены и их длины равны.

Понятие равных векторов дает нам возможность рассматривать векторы без привязки к конкретным точкам. Другими словами, мы имеем возможность заменить вектор равным ему вектором, отложенным от любой точки.

Пусть и два произвольных вектора на плоскости или в пространстве. Отложим от некоторой точки O плоскости или пространства векторы и . Лучи OA и OBобразуют угол .

Определение.

Угол называется углом между векторами и .

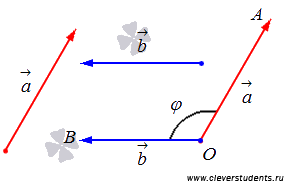
Угол между сонаправленными векторами равен нулю градусам (или нулю радиан), а угол между противоположно направленными векторами равен 180 градусам (или радиан).

Определение.

Два вектора называются перпендикулярными, если угол между ними равен 90градусам (или радиан).

7. ВЕКТОРНОЕ ПРОСТРАНСТВО

матем. понятие, обобщающее понятие совокупности всех (свободных) векторовобычного трёхмерного пространства.

Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действит. числа (см. Векторное исчисление).В применении к любым векторам

x, у, z и любым числам альфа, бета эти правила удовлетворяют след, условиям (условия А):

1) х+у=у+х (перестановочность сложения);

2) (x+y)+z=x+(y+z) (ассоциативность сложения);

3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию

x + 0=x для любого вектора х;

4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0;

5) 1*х=х;

6) (ассоциативность умножения);

7) (распределит, свойство относительно числового множителя);

8) (распределит, свойство относительно векторного множителя).

Векторным (или линейным) пространством наз. множество R, состоящее из элементов любой природы (называемых векторами), в к-ром определены операции сложения элементов и умножения элементов на действит. числа, удовлетворяющие условиям А (условия 1-3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу).

Выражение

(1)

наз. линейной комбинацией векторов e1, е2, ..., еn с коэффициентами a1, a2, ..., an. Линейная комбинация (1) наз. нетривиальной, если хотя бы один из коэффициентов a1, a2, ..., an отличен от нуля. Векторы e1, е2, ..., еn наз. линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e1, е2, ..., еn равна нулевому вектору) векторы e1, е2, ..., еnназ. линейно независимыми.

Векторы (свободные) трёхмерного пространства удовлетворяют след, условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми).

В. п. наз. n-мерным (или имеет "размерность n"), если в нём существуют п линейно независимых элементов e1, е2, ..., еn а любые n+ 1 элементов линейно зависимы (обобщённое условие В). В. п. наз. бесконечномерным, если в нём для любого натурального п существует п линейно независимых векторов. Любые п линейно независимых векторов n-мерного В. п. образуют базис этого пространства. Если e1, е2, ..., еn- базис В. п., то любой вектор х этого пространства может быть представлен единств, образом в виде линейной комбинации базисных векторов:

При этом числа a1, a2, ..., an наз. координатами вектора х в данном базисе.

Примеры В. п. Множество всех векторов трёхмерного пространства образует, очевидно, В. п. Более сложным примером может служить т. н. п-мерное арифметич. пространство. Векторами этого пространства являются упорядоченные системы изп действит. чисел: Сумма двух векторов и произведение на число определяются соотношениями:

Базисом в этом пространстве может служить, напр., след, система из п векторов e1=(l,0,...,0), е2 = (0,1, ..., 0), ..., еn = (0, 0, ..., 1).

Множество R всех многочленов a0 + a1u +... + anun (любых степеней п) от одного переменного с действит. коэффициентами а0, at, ..., сел с обычными алгебр, правилами сложения многочленов и умножения многочленов на действит. числа образует В. п. Многочлены 1, n, n2, ..., nn (при любом п) линейно независимы в R,поэтому R - бесконечномерное В. п.

Многочлены степени не выше п образуют В. п. размерности n + 1; его базисом могут служить многочлены 1, u, u2, ..., un.

Подпространства В. п. В. п. R’ наз. подпространством R, если (то есть каждый вектор пространства R’ есть и вектор пространства R) и если для каждого вектора и для каждых двух векторов v1 и v2 вектор (при любом ) и вектор v1 и v2 один и тот же независимо от того, рассматриваются ли векторы v, v1, v2 как элементы пространства R’ или R. Линейной оболочкой векторов x1, x2, ..., xp наз. множество всевозможных линейных комбинаций этих векторов, т. е. векторов вида a1x1+a2x2+ ... + apxp. В трёхмерном пространстве линейной оболочкой одного ненулевого вектора x1будет, очевидно, совокупность всех векторов, лежащих на прямой, определяемой вектором x1 Линейной оболочкой двух не лежащих на одной прямой векторов x1 и x2 будет совокупность всех векторов, расположенных в плоскости, к-рую определяют векторы x1 и x2. В общем случае произвольного В. п. R линейная оболочка векторов x1, x2, ..., xр этого пространства представляет собой подпространство пространства R размерности р. В n-мерном В. п. существуют подпространства всех размерностей, меньших р. Всякое конечномерное (данной размерности k) подпространство R’ В. п. R есть линейная оболочка любых k линейно независимых векторов, лежащих в R’. Пространство, состоящее из всех многочленов степени (линейная оболочка многочленов 1, u, u2, ..., un), есть (n+1)-мерное подпространство пространства R всех многочленов.

Евклидовы пространства. Для развития геом. методов в теории В. п. нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т. п. Один из возможных путей заключается в том, что любым двум векторам х и уиз R ставится в соответствие число, обозначаемое (х, у) и наз. скалярным произведением векторов х и у. При этом требуется, чтобы выполнялись след, аксиомы скалярного произведения:

1) (x,y) = (x,y) (перестановочность);

2) (x1+x2,y) = (x1,y) + (x2,y) (распределит, свойство);

4) (х,х)>=0 для любого х, причем (х, x)=0 только для х=0.

Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. В. п., в к-ром определено скалярное произведение, удовлетворяющее перечисленным аксиомам, наз. евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно наз. гильбертовым пространством. Длина вектора х и угол между векторами х и у евклидова пространства определяются через скалярное произведение формулами

Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мерное (арифметическое) пространство Еn получим, определяя в

и-мерном арифметич. В.п. скалярное произведение векторов и у - соотношением

(2)

При этом требования 1) -4), очевидно, выполняются.

В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у наз. ортогональными, если их скалярное произведение равно нулю: (х, у) = 0. В рассмотренном пространстве Еn условие ортогональности векторов и как

N-мерные векторы и действия над ними

Множество чисел пронумерованное с помощью натуральных числе и расставленных в порядке возрастания их номеров называется числовой последовательностью.

Общая характеристика вектора

N-мерным вектором называется последовательность чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора.