5. Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура сла́у) в линейной алгебре — это система уравнений вида
|
(1) |
Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.
Здесь — количество уравнений, а — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения втождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть
записана в виде:
x1
+
x2 
+
… + xn 
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Однородные системы линейных уравнений
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:
Тогда n - r линейно независимыми вектор-решениями будут:
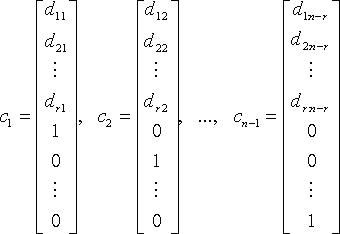
а любое
другое решение является их линейной
комбинацией. Вектор-решения 
образуют
нормированную фундаментальную систему.
В
линейном пространстве 
множество
решений однородной системы линейных
уравнений образует подпространство
размерности n - r;
-
базис этого подпространства.
Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.
линейной
однородной системы обыкновенных
дифференциальных уравнений - базис
векторного пространства действительных
(комплексных) решений этой системы.
(Система может состоять и из одного
уравнения.) Более подробно это определение
формулируется следующим образом.
Множество
действительных (комплексных) решений
{x1(t),...,xn(t)}(заданных на нек-ром множестве
Е)линейной однородной системы обыкновенных
дифференциальных уравнений наз. Ф. с.
р. этой системы уравнений (на множестве
Е) при выполнении совокупности
следующих двух условий: 1) если
действительные (комплексные) числа
С 1,..., С n таковы, что функция
C1x1(t)+...+Cnxn(t) тождественно равна нулю
на Е, то все числа С 1,..., С n равны
нулю; 2) для всякого действительного
(комплексного) решения х(t)рассматриваемой
системы уравнений найдутся действительные
(соответственно комплексные) числа
С 1,..., С n (не зависящие от
t)такие, что x(t) = C1x1(t)+...+Cnxn(t) при
всех 
Если 
-произвольная
невырожденная 
-матрица,
а {x1(t), ..., х п(t)}есть Ф. с. р., то 
также
есть Ф. с. р.; всякая Ф. <с. <р. получается
таким преобразованием из данной Ф. с.
р.
Если система дифференциальных
уравнений имеет вид
где 
(или 
а 
(соответственно 
причем
отображение 
суммируемо
на каждом отрезке, содержащемся в 
-
конечный или бесконечный интервал
в 
то
векторное пространство решений этой
системы изоморфно 
(соответственно 
Следовательно,
система (1) имеет бесконечно много Ф. с.
р., и каждая такая Ф. с. р. состоит из пре
шений. Напр., для системы
уравнений
произвольная
Ф. с. р. имеет вид
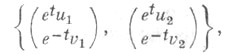
где 
-произвольные
линейно независимые векторы-столбцы.
Всякая
Ф. с. р. системы (1) имеет вид
где 
- Коши
оператор системы (1), 
-
произвольное фиксированное число из
интервала 
а
x1, . . ., х п - произвольный
фиксированный базис
пространства 
(соответственно 
Если
система дифференциальных уравнений
состоит из одного уравнения
где
функции
суммируемы
на каждом отрезке, содержащемся
в 
(где 
-
конечный или бесконечный интервал
в 
то
векторное пространство решений этого
уравнения изоморфно 
(соответственно 
Следовательно,
уравнение (2) имеет бесконечно много Ф.
с. р., и каждая из них состоит из kрешений.
Напр., уравнение 
имеет
Ф. с. р. 
общее
действительное решение этого уравнения
дается формулой 
где
C1, С2 - произвольные действительные
постоянные.
Если система
дифференциальных уравнений имеет вид
где 
(или 
)
и при всяком i = l, ..., k-1 отображение
суммируемо
на каждом отрезке, содержащемся
в 
(где 
-конечный
или бесконечный интервал в 
то
пространство решений этой системы
уравнений изоморфно 
(соответственно 
Ф.
с. р. системы (3) существуют, и каждая из
них состоит из kn решений.
Для
линейных однородных систем дифференциальных
уравнений, не разрешенных относительно
старших производных, даже если коэффициенты
системы постоянные, число решений,
входящих в Ф. с. р. (т. е. размерность
векторного пространства решений),
вычисляется иногда не столь просто, как
в вышеприведенных случаях. (В [1], з 11
рассмотрено такое вычисление для
линейных систем дифференциальных
уравнений с постоянными коэффициентами,
не разрешенных относительно старших
производных.)