
- •Движение свободного твердого тела.
- •Задание движения свободного твердого тела.
- •Скорости и ускорения точек свободного твердого тела.
- •17. Основные аксиомы статики. Сложение сходящихся сил.
- •2)Центр параллельных сил
- •2)Определение координат тяжести однородного тела
- •Теоретическая механика кинематика
- •1.2. Первая задача динамики свободной точки
- •1.3. Вторая задача динамики свободной точки
- •2) Импульс силы
1.2. Первая задача динамики свободной точки
Первой или прямой называется задача, в которой заданы масса точки и закон ее движения в декартовых координатах или в естественной форме. Необходимо определить модуль и направление силы, действующей на точку.
Для решения задачи надо выполнить следующие операции:
– построить расчетную схему, на которой в соответствии с условием задачи изобразить систему осей координат, нарисовать траекторию точки и отметить на траектории то положение точки, для которого требуется найти действующую силу. Эту силу следует представить составляющими на выбранные оси координат;
– по заданному движению материальной точки определить проекции ее ускорения на принятые оси координат;
– составить дифференциальные уравнения движения материальной точки в форме (1.2) или (1.3) и из полученных уравнений определить проекции искомой силы, а затем ее модуль и направляющие косинусы.
1.3. Вторая задача динамики свободной точки
Второй или обратной называется задача, в которой по заданным силам и массе материальной точки определяется ее движение. Для решения задачи надо выполнить следующие операции.
● Построить
расчетную схему. Для этого прежде всего
надо выбрать систему координат. В случае
произвольного движения точки в
пространстве следует выбрать систему
координат
![]() .
Положение начала координат
.
Положение начала координат
![]() указывается
в условии задачи или выбирается в
начальном положении движущейся
материальной точки.
указывается
в условии задачи или выбирается в
начальном положении движущейся
материальной точки.
● Затем
в принятой системе координат надо
изобразить предполагаемую траекторию
точки и отметить на ней начальное
положение точки
![]() ,
изобразить начальную скорость
,
изобразить начальную скорость
![]() .
Следует отметить также произвольное
положение точки
.
Следует отметить также произвольное
положение точки
![]() ,
обозначить ее координаты
,
обозначить ее координаты
![]() ;
изобразить все силы, действующие на
материальную точку в этом произвольном
положении. Если точка движется по
плоскости, то следует выбирать систему
координат
;
изобразить все силы, действующие на
материальную точку в этом произвольном
положении. Если точка движется по
плоскости, то следует выбирать систему
координат
![]() .
Для прямолинейного движения материальной
точки достаточно выбрать одну координатную
ось, которая совмещается с траекторией
точки; при этом за положительное
направление оси следует принять
направление начальной скорости
.
.
Для прямолинейного движения материальной
точки достаточно выбрать одну координатную
ось, которая совмещается с траекторией
точки; при этом за положительное
направление оси следует принять
направление начальной скорости
.
Уточнить
начальные условия движения точки, т. е.
из условия задчи при
![]() определить
определить
![]() –
координаты точки в начале движения;
–
координаты точки в начале движения;
![]() –
проекции начальной скорости на оси
координат.
–
проекции начальной скорости на оси
координат.
Составить дифференциальные уравнения движения точки в форме (1.2):
![]()
– это дифференциальные уравнения второго порядка.
Определить законы движения вдоль координатных осей; т. е. найти вторые интегралы уравнений (1.2):
![]()
![]()
![]()
Постоянные
интегрирования
![]() находятся
с использованием начальных условий
обычными для теории дифференциальных
уравнений способами.
находятся
с использованием начальных условий
обычными для теории дифференциальных
уравнений способами.
Основные виды дифференциальных уравнений и их интегрирование даны в приложении.
В некоторых задачах, особенно при исследовании прямолинейного движения точки, требуется определить закон изменения скорости. В таких случаях достаточно найти только первые интегралы дифференциальных уравнений движения точки (см. задачу 1.2 (1)).
Задача
1.2 (1).
Материальная точка массой
![]() движется
вдоль горизонтальной прямой под действием
силы, изменяющейся по гармоническому
закону
движется
вдоль горизонтальной прямой под действием
силы, изменяющейся по гармоническому
закону
![]() и
направленной вдоль этой прямой. Найти
закон движения точки, если при
скорость
точки равна нулю.
и
направленной вдоль этой прямой. Найти
закон движения точки, если при
скорость
точки равна нулю.
Решение
Расчетная
схема дана на рис. 1.2. Примем за координатную
ось
![]() горизонтальную
прямую, а положение точки при
–
за начало координат
.
горизонтальную
прямую, а положение точки при
–
за начало координат
.
|
Изобразим материальную
точку в произвольном положении на
расстоянии
На
точку действуют
Начальные
условия:
Составим дифференциальное уравнение движения в форме (1.2):
|
Это уравнение относится к виду (1) приложения.
Так
как
![]() ,
то
,
то
![]() .
.
Разделив
переменные, получим
![]() .
Интеграл этого уравнения
.
Интеграл этого уравнения
![]() .
.
Используя
начальные условия
![]() ,
найдем
,
найдем
![]() .
.
Теперь
будем иметь
![]() .
.
Заменив
![]() на
на
![]() и
разделив переменные, получим
и
разделив переменные, получим
![]() .
.
Интегрирование последнего уравнения дает:
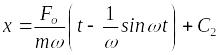 .
.
Используя
начальные условия
![]() ,
найдем
,
найдем
![]() .
.
Окончательно будем иметь
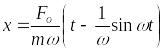 .
.
№32 Теорема об изменении количества движения мат. точки, Импульс силы.

