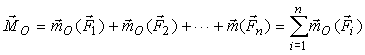17. Основные аксиомы статики. Сложение сходящихся сил.

Система сил, приложенная к телу или материальной точке, называется уравновешенной или эквивалентной нулю, если тело под действием этой системы находится в состоянии покоя или движения по инерции.^[1]

1. Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.

2. О действии и противодействии. При всяком действии одного тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению.

3. О двух силах. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.

4. О равнодействующей. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.

5. Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его затвердевания.

6. Аксиома о связях. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.

Следствия

1. При переносе силы вдоль её линии действия, действие этой силы на тело не меняется.

2. Сумма всех внутренних сил равна нулю.

18. Сложение параллельных сил. Пара сил

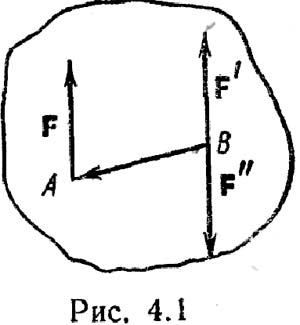
Пара сил. Если на тело действует несколько сил, равнодействующая которых равна нулю, а результирующий момент относительно какой-либо оси не равен нулю, то тело не останется в равновесии. Так будет, например, если на тело действуют две равные и противоположные силы, не лежащие на одной прямой.

Такие две   силы,   совместно действующие  на  тело, называют парой сил. Если тело закреплено на оси,   то при действии на него пары сил оно начнет вращаться вокруг этой оси. При этом, вообще говоря, со стороны оси на тело будет действовать сила. Можно показать, однако, что если ось проходит через определенную точку тела, то сила со стороны оси отсутствует. Поэтому, если пара сил будет действовать на свободное тело, то оно начнет вращаться вокруг оси, проходящей через эту точку. Можно доказать, что эта точка — центр тяжести тела (см. следующий параграф).

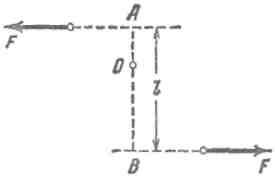
Рис. 122. Момент пары сил M=Fl.

Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Действительно, пусть О — произвольная ось, перпендикулярная к плоскости, в которой лежит пара (рис. 122). Суммарный момент М равен

M = F•OA + F•OB = F(OA + OB) = F•l,

где l — расстояние между силами, составляющими пару. Этот же результат получится и при любом другом положении оси. Можно показать также, что момент нескольких сил, равнодействующая которых равна нулю, будет один и тот же относительно всех осей, параллельных друг другу, и поэтому действие всех этих сил на тело можно заменить действием одной пары сил с тем же моментом.

19. Момент силы относительно точки и момент силы относительно оси.

 

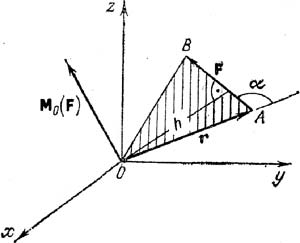
Моментом силы относительно  точки (центра) на­зывается вектор, численно равный произведению модуля силы на плечо, т. е. на кратчайшее расстояние от указанной точки до линии дей­ствия силы. Он направлен перпендикулярно плоскости, проходя­щей через выбранную точку и линию действия силы. Если мом силы по часов стрелки, то момент отрицательный, а если против, то положительный. Если O— точка, относ кот находится момент силы F, то момент силы обозначается символом М_о(F). Если точка приложения силы F определяется радиусом-вектором r относительно О, то справедливо соотношение М_о(F)=г х F. (3.6) Т.е. момент силы равен векторному произ­ведению вектора r на вектор F. Модуль   векторного   произведения   равен М_о(F)=rF sin a=Fh, (3.7) где h — плечо силы. Вектор М_о(F) направлен перпендикулярно плоскости, проходящей через векторы r и F, и против часовой стрелки. Таким образом, формула (3.6) полностью определяет модуль и направление момента силы F. Формулу (3.7) можно записать в виде M_O(F)=2S, (3.8) где S– площадь треугольника ОАВ. Пусть x, у, z — координаты точки приложения силы, a F_x, F_y, F_z — проекции силы на координатные оси. Если т. О нах. в начале координат, то момент силы:

Значит, проекции момента силы на координатные оси определяются ф-ми: M_ox(F)=yF_z–zF_y, M_oy(F)=zF_x–xF_z, M_oz(F)=xF_y–yF_x (3.10).

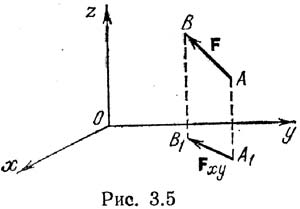
Введем понятие проекции силы на плоскость. Пусть дана сила F и нек-ая пл-ть. Опустим из начала и конца вектора силы перпендикуляры на эту плоскость (рис. 3.5). Проекцией силы на плоскость называется вектор, начало и конец которого совпадают с проекцией начала и проекцией конца силы на эту  плоскость. Проекцией силы F на пл-ть xOy будет F_xy.Момент силы F_xy отн. т. О (если z=0, F_z=0) будет M_o(F_xy)=(xF_y–yF_x)k. Этот момент направлен вдоль оси г, а его проек­ция на ось z в точности совпадает с проекцией на ту же ось момента силы F относительно точки О.Т.е, M_Oz(F)=М_Оz(F_xy)=xF_y–yF_x. (3.11). Тот же результат мож­но получить, если спроектировать силу F на любую другую плоскость, парал­лельную плоскости хОу. При этом точка пересечения оси с плоскостью будет уже иной (обозначим О₁). Однако все входящие в правую часть равенства (3.11) величины х, у, F_x, F_y останутся неизменными: M_Oz(F)=M_Olz(F_xy). Проекция момента силы относительно точки на ось, проходящую через эту точку, не зависит от выбора точ­ки на оси. Вместо M_Oz(F) запишем M_z(F). Эта проекция момента называется моментом силы относительно оси z. Перед вычислениями силу F проецируют на пл-ть, перп оси. М_z(F)=М_z(F_xy)=±F_xyh (3.12). h- плечо. Если по часовой стрелки, то +, против –. Для вычисления мом. сил нужно: 1) выбрать на оси произвольную точку и построить плоскость,  перпендикулярную оси; 2)  спроектировать   на эту плоскость силу; 3)  определить плечо проекции силы h. Момент силы относительно оси равен произведению модуля про­екции силы на ее плечо, взятому с соответствующим знаком. Из (3.12) следует, что момент силы относительно оси равен нулю: 1) когда проекция силы на плоскость, перпендикулярную оси, равна нулю, т. е. когда сила и ось параллель­ны; 2) когда плечо проекции h равно нулю, т. е. когда линия действия силы пересекает ось. Или: мо­мент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось находятся в одной плоскости.

20. Теоремы об эквивалентности пар

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Доказательство: Пусть на твердое тело действует пара сил .

Перенесем силу  в точку , а силу  в точку . Проведем через точки две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки  отрезком прямой и разложим силы в точке  и  в точке  по правилу параллелограмма.

Так как , то

и

Поэтому эквивалентна системе , а эта система эквивалентна системе , так как эквивалентна нулю.

Таким образом мы заданную пару сил  заменили другой парой сил . Докажем, что моменты у этих пар сил одинаковы.

Момент исходной пары сил  численно равен площади параллелограмма , а момент пары сил  численно равен площади параллелограмма . Но площади этих параллелограммов равны, так как площадь треугольника равна площади треугольника .

Что и требовалось доказать.

Выводы:

1.      Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.

2.      У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.

№21.Сложение пар на плоскости и в пространстве.(?)

№22. Теорема о параллельном переносе силы.

Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, параллельно перенести в любую другую точку тела, добавив при этом пару сил с моментом, равным моменту переносимой силы относительно ее новой точки приложения. Докажем эту теорему.

Пусть в точке А приложена сила, которую мы хотим перенести в точку В. Приложим в точке В уравновешенную систему двух сил, равных по величине переносимой силе, как показано на рисунке. Заменив образовавшуюся при этом пару сил   (которую называют присоединенной) ее моментом и перенеся данный момент, как свободный вектор, в точку В, получаем формулируемое в теореме утверждение.

  Рис. 1.24. Эквивалентные преобразование при параллельном переносе силы

Задание на контрольную работу Техническая механика

Пример 1.

 На барабан 1 радиуса r намотаны в противоположных направлениях две нити, к концам которых прикладывают силы   и  . На барабан 2 того же радиуса намотана одна нить, к которой прикладывают силу  (рис. 1.29). Рассмотрим, чем будут отличаться действия этих сил.

 

 Рис. 1.29. Примеры действия пар сил

На барабан 1 действует только пара сил   с моментом, численно равным 2rF, вращающим барабан. Силу, действующую на барабан 2, можно заменить силой  , приложенной к оси барабана, и парой сил   с моментом 2rF . Итак, оба барабана будут вращаться одинаково. Но при этом ось второго барабана будет испытывать давление, равное 2F, а ось первого барабана никакого давления не испытывает.

№ 22 Теорема о параллельном переносе силы

Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.(№22)

№23

Пусть на тело действует система произвольно направленных, лежащих в одной плоскости сил .

Выберем в плоскости произвольную точку О, которую назовем центром приведения и перенесем в эту точку все силы (рис. 29, а )

В результате получим новую систему сил:

с моментами присоединенных пар:

Систему сил перенесенную в точку О заменим одной силой приложенной в той же точке О:

Сложение пар дает одну пару с моментом:

Вектор , равный геометрической сумме всех сил называют главным вектором системы. Величину , равную сумме всех моментов относительно центра О, называют главным моментом системы относительно центра О.

Итак: Всякая плоская система сил, действующая на твердое тело при приведении к произвольно взятому центру О заменяется одной силой , равной главному вектору системы и приложенной в Центре приведения О, и одной парой с моментом , равным главному моменту системы сил относительно центра О.

Для задания плоской системы сил достаточно задать ее главный вектор и главный момент относительно некоторого центра О. Главный вектор не зависит от положения центра приведения O (рис. 29, б).

Главный момент зависит от положения центра приведения О и его всегда нужно указывать.

При приведении произвольно расположенных сил на плоскости к данному центру возникают стандартные случаи, называемые приведением системы к простейшему виду. Рассмотрим эти случаи, имея в виду, что определено согласно (4.2.3), а согласно (4.2.4):

Все силы, приложенные к твердому телу, уравновешиваются.

Все силы приводятся к одной паре сил.

Все силы приводятся к равнодействующей.

Заданная система сил так же приводится к равнодействующей.

№23(Главный вектор.)

Рассмотрим плоскую систему сил (F₁, F₂, ..., F_n),действующих на твердое тело в координатной плоскости Oxy.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F₁ + F₂ + ... + F_n = F_i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О:

L_O = M_O(F₁) + M_O(F₂) + ... + M_O(F_n) = M_O(F_i).

Вектор R не зависит от выбора центра О, а вектор L_O при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом L_O плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

№23 Приведение различных пространственных систем к центру.

Теорема о приведении системы сил:

Любая система сил, действующих на абсолютно твердое тело, может быть заменена одной силой R, равной главному вектору этой системы сил и приложенной к произвольно выбранному центру О, и одной парой сил с векторным моментом L_O, равным главному моменту системы сил относительно центра О.

Такая эквивалентная замена данной системы сил силой R и парой сил с моментом L_O называют приведением системы сил к центу О.

В результате приведения пространственной системы сил к произвольному центру О возможны следующие случаи, зависящие от векторов R и L_O:

1. если R = 0, L_O = 0, то заданная система является равновесной;

2. если хотя бы одна из величин R или L_O не равна нулю, то система сил не находится в равновесии. При этом:

   • E сли R = 0 и L_O 0, то система сил приводится к одной паре сил с моментом L_O. В этом случае величина момента L_O не зависит от выбора центра О.

   • Eсли R 0, L_O = 0, то система сил приводится к равнодействующей силе R^* = R, линия действия которой проходит через центр О.

   • Eсли R 0, L_O 0 и эти векторы взаимно перпендикулярны, то система сил также приводится к равнодействующей силе R^* = R, но линия ее действия не проходит через центр О.

№24 Перемена центра приведения пространственной системы сил.

До формулировки и доказательства теоремы дадим понятия главного вектора и главного момента системы сил.

Главным вектором системы сил называют вектор, равный сумме всех сил системы:

(2)

Главным моментом системы сил относительно центра называют вектор, равный сумме моментов всех сил системы относительно центра:

(3)

Сформулируем основную теорему статики.

Произвольная система сил, приложенная к твердому телу, эквивалентна одной силе, приложенной в центре приведения и равной главному вектору, и одной паре сил, момент которой равен главному моменту относительно центра приведения:

(4)

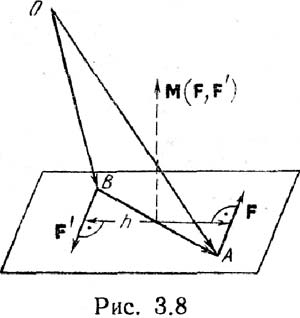
Докажем теорему. Пусть к твердому телу приложена произвольная система сил (F₁, F₂, ..., F_n). Какую либо точку тела выберем за центр приведения и обозначим буквой O. Следуя лемме, силы системы переносим в эту точку и получаем систему пар сил и пучок сил в центре приведения. Складывая все силы пучка и пары сил, получаем одну силу в центре приведения и одну пару сил. Силы пучка по величине и направлению равны силам исходной системы, поэтому полученная сила равна главному вектору системы R. Моменты пар равны моментам соответствующих сил относительно центра O, поэтому момент полученной пары сил (F,F') равен главному моменту системы M_O. Теорема доказана.

Заметим, что при параллельном переносе сил к центру приведения не изменились ни модули, ни направления сил, поэтому главный вектор не зависит от выбора центра приведения. Главный вектор является инвариантом (неизменной величиной) данной системы сил. В отличие от главного вектора, главный момент зависит от выбранного центра приведения и не является инвариантом.

№25 Привидение системы сил к одной силе, к одной паре

Проси другой билет.(

№26 Условие равновесия произвольной пространственной системы сил.

Теорема.Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю.Достаточность: при F_o=0 система сходящихся сил, приложенных в центре при­ведения О, эквивалентна нулю, а при М_о=0 система пар сил эквивалентна нулю. Следовательно, исходная система сил эквива­лентна нулю. Необходимость: Пусть данная система сил эквивалентна нулю. Приведя систему к двум силам, заметим, что система сил Q и Р (рис. 4.4) должна быть эк­вивалентна нулю, следовательно, эти две силы должны иметь общую линию действия и должно выполняться рав-во Q=–Р. Но это может быть, если линия действия силы Р проходит через точку О, т. е. если h=0. А это значит, что главный момент равен нулю (М_о=0). Т.к. Q+Р=0, a Q=F_o+P', то F_o+P'+P=0, и, следовательно, F_o = 0. Необх и дост усл равнов про­странственной сист сил им вид: F_o=0, M_o=0 (4.15),

или, в проекциях на координатные оси, Fox=åF_kx=F_1x+F_2x+…+F_nx=0; F_Oy=åF_ky=F_1y+F_2y+...+F_ny=0; F_oz=åF_kz=F_1z+F_2z+…+F_nz=0 (4.16). M_Ox=åM_Ox(F_k)=M_Ox(F₁)+М_ox (F₂)+...+M_Ox(F_n)=0, M_Oy=åM_Oy(F_k)=M_oy(F₁)+M_oy(F₂)+…+M_oy (F_n)=0, М_oz=åМ_Оz(F_k)=М_Оz(F₁)+M_oz (F₂)+...+М_oz(F_n)=0. (4.17)

Т.о. при решении задач имея 6 ур-ий можно найти 6 неизвестных. Замечание: пару сил нельзя привести к равнодействующей. Частные случаи: 1) Равновесие пространственной системы параллельных сил. Пусть ось Z параллельна линиям действ силы (рис 4.6), тогда проекции сил на x и y равны 0 (F_kx=0 и F_ky=0), а остаётся только F_oz. А что касается моментов, то остаются только M_ox и M_oy, а M_ozотсутствует. 2) Равновесие плоской системы сил. Остаются ур-я F_ox, F_oy и момент M_oz (рис 4.7). 3) Равновесие плоской системы параллельных сил. (рис. 4.8). Остаются только 2 ур-я: F_oy и M_oz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка.

№27 Теорема от 3х непараллельных силах

Вначале сформулируем теорему, а затем ее докажем.

Если под действием трех сил твердое тело находится в равновесии и линии действия двух сил пересекаются в одной точке, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

П усть на твердое тело действует система трех сил F₁, F₂ и F₃, причем линии действия первых двух пересекаются в точке A (рис. 11, a). Согласно следствию из второй аксиомы, силы F₁, F₂ переносим в точку A(рис. 11, b). Следуя третьей аксиоме, сложим их, заменив их одной силой, равной R=F₁+F₂. Таким образом, исходная система сил приведена к двум силам R и F₃ (рис. 11, c).

Тело находится в равновесии. Поэтому, по первой аксиоме силы R и F₃ должны иметь общую линию действия. Это может быть только тогда, когда исходные три силы лежат в одной плоскости, а линии действия сил пересекаются в одной точке. Теорема доказана.

Теорема о трех силах позволяет в ряде задач найти линию действия неизвестной силы, приложенной к твердому телу.

Система сходящихся сил.

Напомним определение системы сходящихся сил. Система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Используя только аксиомы статики, рассмотрим приведение системы сходящихся сил и найдем условия равновесия твердого тела под действием этой системы сил.

Приведение системы сходящихся сил.

Пусть система сходящихся сил (F₁, F₂,...,F_n) приложена к твердому телу (рис. 12, a).

Согласно следствию второй аксиомы, п ереносим все силы системы в точку пересечения линий действия A и получаем систему сил, приложенных в одной точке (рис. 12, b). По аксиоме параллелограмма сил, начиная с сил F₁ и F₂, последовательно складываем силы, добавляя каждый раз к полученной сумме по одной силе системы. Дойдя до последней силы F_n, выясняем, что система сил (рис. 12, b) эквивалентна одной силе или равнодействующей R^* (рис. 12, c), равной геометрической сумме сил системы.

Таким образом, система сходящихся сил приводится к равнодействующей (эквивалентна равнодействующей), которая равна геометрической сумме сил системы и приложена в точке пересечения линий действия сил:

(F1, F2,...,Fn) ~ R*; R* = F1 + F2 + ... + Fn

(1)

Условия равновесия системы сходящихся сил.

Эти условия определяют, когда твердое тело находится в равновесии под действием системы сходящихся сил. Сформулируем условие, а затем докажем его.

Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы геометрическая сумма всех сил системы была равна нулю:

(2)

Необходимость условия сразу следует из (1). При выполнении условия (2) получим R^* = 0, следовательно F₁, F₂,..., F_n ~ 0.

Достаточность условия равновесия докажем методом от противного. Предположим, что условие (2) не выполняется, а твердое тело находится в равновесии. Но если (2) не выполняется, то система сходящихся сил приводится к одной силе, а тело под действием одной силы не может находиться в равновесии. Таким образом, достаточность условия равновесия доказана.

В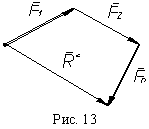 ыражение (2) представляет собой условие равновесия в векторной или геометрической форме. Вспомнив суммирование векторов по правилу векторного многоугольника (рис. 13), формулируем условие равновесия иными словами. На рисунке вектор R^* является суммой векторов и не равен нулю. Но если R^* = 0, то конец последнего вектора попадет в начало первого вектора, и векторный многоугольник, который в нашем случае можно назвать силовым многоугольником, окажется замкнутым.

Следовательно, для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник системы был замкнутым.

Применение условия равновесия в геометрической форме ограничено трудностью построения силового многоугольника в пространстве. Более универсальными являются условия равновесия в аналитической форме. Для получения этих условий выберем систему координат OXYZ, связанную с поверхностью Земли . Проектируя на оси координат векторное равенство (2), имеем F_1x + F_2x +...+ F_nx = 0; F_1y + F_2y +...+ F_ny = 0; F_1z + F_2z +...+ F_nz = 0. Записав эти выражения в компактной форме, получаем

(3)

По математической записи формулируем условия равновесия в аналитической форме для системы сходящихся сил.

Для равновесия твердого тела под действием системы сходящихся сил необходимо и достаточно, чтобы суммы проекций сил системы на оси координат были равны нулю.

В плоской системе сходящихся сил все силы лежат в одной плоскости, например XOY, и третье условие в (3) вырождается в тождество . Отбрасывая его, имеем условия равновесия для плоской системы сходящихся сил в аналитической форме:

№29 Теорема Вариньона. Центр параллельных сил.

Теоре́ма Вариньо́на — одна из теорем механики, устанавливающая зависимость между моментами сил данной системы и моментом их равнодействующей силы относительно какого-либо центра или оси. Сформулирована для сходящихся сил Пьером Вариньоном в 1687, либо, ещё раньше, Симоном Стевином.

Теорема Вариньона:

Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

Векторная запись теоремы: .