12) Способы задания движения точки
В кинематике точки изучаются движения как мат. Тел, так и отдельных точек этих тел
Способы задания:
1)Прямой
– текущее положение M
т.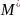
задана как ф-ция времени M=M(t)
2)Векторный-
радиус вектор
текущего положения точки задан как
ф-ция времени
=
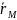(t),
относительно полюса О.
3)Координатный- координаты заданы как ф-ции от времени
=
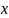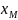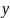(t),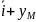
=
(t),
(t)=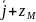
(t)
(t)
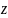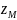(t)
=
(t),
Траектория – ГМ положений движущейся точки в выбранной у.н.С.О. те линия описываемая концом радиус-вектора с изменением t.
Уравнение траектории получается исключением t
4)Естественный-
задают траекторию, начало отсчета,
направление отсчёта, закон изменения
линейной координаты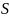
=
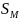(t)
Из аксиомы движения следует, что любая из функций времени в 1)-4) непрерывна
13) Скорость точки в в-ом и координатном способах задания движения
Пусть
t и
,
=
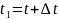(t)-текущий
рад в-р. М и
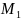положения т.
в моменты t
и
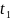
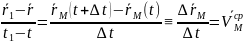средняя скорость
т. на указ врем промеж
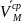направлена вдоль
секущей. Придел
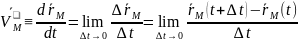-скорость т.
в момент t,
направлена по касательной к траектории
Для
прямого способа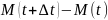
=
,
,
+
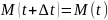Из
последней ф-лы для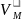
следует, что она не зависит от выбора
полюса О
Иная
запись
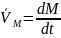
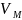(t)=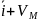
(t)
(t)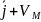
(t)
,
дифференцируя по t
р-во
(t)=
(t)
(t)
(t)
получим
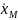(t)=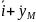
(t)
(t)
(t)
,
в координатном способе
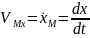и
тд.
Модуль
скорости
14)Скорость при естественном способе задания движения точки
Пусть
траэктория точки- гладкая кривая и при
t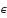
[
]
линейная координата S=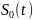
монотонно меняется с изменением t,
тогда можно выразить t,
как ф-цию t=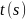
,
тогда можно выразить
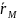представить, как сложную ф-цию
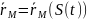тогда:
(*)
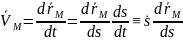Обозначим
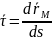
Заметим
что
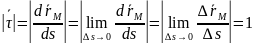
Итак
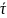еденичный касательный в-р; он направлен
вдоль траэктории, в направлении роста
S.
Из ф-лы (*) получаем: (**)
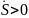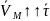(при
,
,
при
,
)
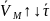Скалярная
величина
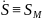алгебраическая
скорость Т(мгновенная алгебраическая
скорость),
;
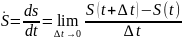под знаком Lim-средняя
алгебраическая скорость на t
[
]
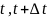Следствие(Эйлера)-модуль скорости точки = модули её алгебраической скорости
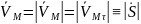Значит
,
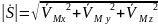так как
,
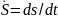то
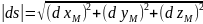Формула
Клеро для дыф-ла линейной координаты
17)Лемма об уравнениях сближения двух точек по экспоненте
Пусть
т
и
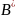сближаются по экспоненте:
(1)
,
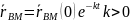те
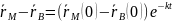при
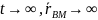
В силу (1) линия визирования MB остаётся || первоначальному направлению => || сближение. Если движение в плоскости Oxy, то
(
)
x=x(0)
,
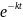y=y(0)
Точки и сближаются по экспоненте их скорости удовлетворяют уравнениям сближения по экспоненте
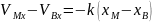
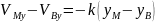
Док-во: 1) Пусть точки сближаются по экспоненте, дифференцируя (1) по t
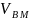=-k
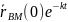Итак,
,
в координатной записи это сводится к
(*)
2) Пусть ур-я (*) выполнены, представим их в виде
(**)
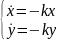
Поставив
для системы дифур (**) задачу Кош(нач
условия x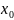(0)=
,
y(0)=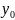
)
Прямой подстановкой (1’) в (**) убеждаемся что ф-лы(1’) дают решение поставленной задачи Коши
x(0)(-k) =-kx(0)
y(0)(-k) =-ky(0)
В силу (1’) т. и сближаются по экспоненте