3. Если сходятся числовые ряды   и  , их суммы равны A и B соответственно, то ряды будут сходящимися, причем их суммы будут равны A + B и A - B соответственно.

4. Остаточные признаки сходимости знакоположительного ряда.

При использовании достаточных признаков для исследования числовых рядов на сходимость постоянно приходится сталкиваться с вычислением пределов, так что рекомендуем обращаться к этому разделу при затруднениях. Необходимое и достаточное условие сходимости знакоположительного числового ряда. Для сходимости знакоположительного числового ряда   необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. Начнем с признаков сравнения рядов. Их суть заключается в сравнении исследуемого числового ряда с рядом, сходимость или расходимость которого известна. №31. Достаточные признаки сходимости (и расходимости) неотрицательных рядов: ограниченность частичных сумм, признаки сравнения, признаки Даламбера и Коши, интегральный признак Коши.

Первый, второй и третий признаки сравнения.

Первый признак сравнения рядов. Пусть   и   - два знакоположительных числовых ряда и выполняется неравенство   для всех k = 1, 2, 3, ... Тогда из сходимости ряда   следует сходимость  , а из расходимости ряда   следует расходимость  . Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть  , разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом  , то есть, гармонический ряд. Рассмотрим несколько примеров. Второй признак сравнения. Пусть   и   - знакоположительные числовые ряды. Если  , то из сходимости ряда  следует сходимость  . Если  , то из расходимости числового ряда   следует расходимость  . Следствие. Если   и  , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость. Исследуем ряд   на сходимость с помощью второго признака сравнения. В качестве ряда  возьмем сходящийся ряд  . Найдем предел отношения k-ых членов числовых рядов: 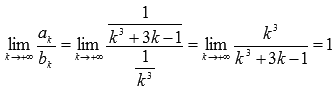  Таким образом, по второму признаку сравнения из сходимости числового ряда   следует сходимость исходного ряда.

Третий признак сравнения. Пусть   и   - знакоположительные числовые ряды. Если с некоторого номера N выполняется условие  , то из сходимости ряда   следует сходимость  , а из расходимости ряда   следует расходимость  .

Признак Даламбера.

Пусть   - знакоположительный числовой ряд. Если  , то числовой ряд сходится, если  , то ряд расходится. Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если  , то ряд расходится. Если  , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Радикальный признак Коши.

Пусть   - знакоположительный числовой ряд. Если  , то числовой ряд сходится, если  , то ряд расходится. Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если  , то ряд расходится. Если  , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Интегральный признак Коши.

Пусть   - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции  . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале  , где  ). Тогда в случае сходимости несобственного интеграла 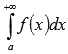  сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.

№32. Знакопеременные ряды. Признак Лейбница для знакочередующегося ряда. Оценка остатка ряда Лейбница.

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда являетсязнакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки.

Признак Лейбница

Для знакочередующихся рядом действует достаточный признак сходимости Лейбница.  Пусть {a_n} является числовой последовательностью, такой, что

1. a_n+1 < a_n для всех n;  2.  .

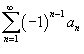Тогда знакочередующиеся ряды   и   сходятся.

Абсолютная и условная сходимость

Ряд   называется абсолютно сходящимся, если ряд   также сходится.  Если ряд   сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.  Ряд   называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. 

Остаток ряда и его оценка

Рассмотрим сходящийся числовой ряд

           (23)

Вычисление суммы ряда S=  обычно технически очень сложно. Поэтому в качестве S берут S≈S_n. Точность этого равенства возрастает с увеличением n.

Определение 7. Если числовой ряд сходится, то разность R_n=S-S_n называется n-м остатком ряда.

Таким образом, R_n представляет собой сходящийся числовой ряд:

R_n= u_n+1+u_n+2+… .

Заметим, что  R_n= ( S-S_n)=S-S=0.

Абсолютная погрешность при замене суммы ряда S его частичной суммой S_n равна |R_n|=|S-S_n|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа nпервых членов ряда, чтобы выполнялось условие |R_n|<E. Однако в общем случае находить точно R_n не удаётся.

№33. Абсолютная и условная сходимость знакопеременных рядов. Формулировка свойств абсолютно и условно сходящихся рядов. Признаки Даламбера и Коши для знакопеременных рядов.

Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.

Знакопеременный ряд  сходится, если сходится ряд .

В этом случае знакопеременный ряд  называют абсолютно сходящимся.

Сходящийся знакопеременный ряд  называют условно сходящимся, если ряд  расходится.   1) Теорема. Для абсолютной сходимости ряда необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.

 

  Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами.

1. В абсолютно сходящемся ряде последовательность членов может быть изменена любым образом, при этом характер сходимости ряда и величина его суммы не изменятся. Сходящиеся ряды, суммы которых не зависят последовательности членов, называют безусловно сходящимися.

Если ряд сходится условно, а σ — любое заданное число, то члены ряда можно так переупорядочить, что преобразованный ряд будет сходится, и число σ будет его суммой (теорема Римана).

2. Под произведение двух бесконечных рядов 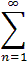a_n и b_n понимают ряд, образованный из всевозможных произведений a_n b_k (n, k = 1, 2, …). Эти произведения a_n b_k можно упорядочить многими способами и получить тем самым различные ряды. Следующая теорема Коши дает условие того, чтобы все эти ряды сходились и имели одну и ту же сумму.

Теорема Коши. Если ряды a_n и b_n сходятся абсолютно и имеют суммы A и B соответственно, то все их произведения также сходятся абсолютно и имеют сумму A·B. В этом случае справедлива формула

             a_n b_n = a_m b_{m – n}

(формула умножения Коши).

Формула умножения Коши имеет место и тогда, когда один из двух рядов a_n или b_n сходится абсолютно, а другой ряд просто сходится. Ряд–произведение в этом случае просто сходится, но не абсолютно.

Признак Даламбера.

Пусть   - знакоположительный числовой ряд. Если  , то числовой ряд сходится, если  , то ряд расходится. Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если  , то ряд расходится. Если  , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

№34. Степенные ряды. Теорема Абеля. Теорема об области сходимости степенного ряда. Свойства степенных рядов в области сходимости. Арифметические операции над степенными рядами.

Определение

Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:

Теорема 1.1. (теорема Абеля). Если степенной ряд (1.2) сходится при некотором  , где -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что   Наоборот, если ряд (12) расходится при  , то он расходится при всех значениях x таких, что   

Доказательство. Пусть числовой ряд

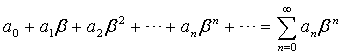   (1.3) 

сходится. Поэтому   Но любая последовательность, имеющая предел, ограничена, значит, существует такое число M, что   для всехn=0,1,2,…

Рассмотрим теперь ряд

   (1.4) 

предполагая, что   Так как 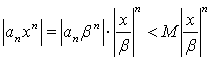  и при этом   то члены ряда (3.4) не превосходят соответствующих членов сходящегося ряда

 

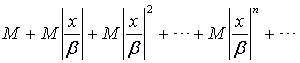
(геометрической прогрессии). Следовательно, ряд (1.4) сходится, а ряд (1.2) абсолютно сходится.

Предположим теперь, что ряд (1.3) расходится, а ряд (1.2) сходится при    Но тогда из сходимости ряда (1.2) следует сходимость и ряда (1.3), что противоречит предположению. Теорема доказана.

Теорема Абеля позволяет дать описание области сходимости степенного ряда.

Теорема (Область сходимости степенного ряда).

«Если существует предел , то степенной ряд

(1) сходится абсолютно в области ( внутри круга радиуса r с центром в точке z₀ на комплексной плоскости; внутри отрезка (х₀-r, х₀+ r) – на числовой прямой)

и (2) расходится в области .»

Док-во теоремы следует из признаков Коши и Даламбера абсолютной сходимости числового ряда : 

Замечания.

1. Неотрицательное число r=1/q называется «радиусом сходимости степенного ряда».

Очевидно, что , т.е. существуют степенные ряды, сходящиеся только в одной точке(r=0), сходящиеся внутри круга конечного радиуса (0<r<)и сходящиеся на всей комплексной плоскости ( на всей числовой оси) (r=).

2. Сходимость числовых рядов в точках окружности или на концах интервала – в точках х1=x₀ - r; x2=x₀ + r, необходимо исследовать отдельно.

№35. Ряды Тейлора и Маклорена. Теорема о единственности разложения. Теорема о необходимых и достаточных условиях разложимости; теорема о достаточных условиях разложимости функции в ряд Тейлора.

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

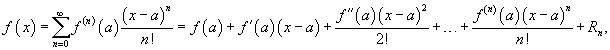
где R_n − остаточный член в форме Лагранжа определяется выражением

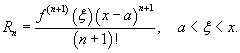
Если приведенное разложение сходится в некотором интервале x, т.е.  , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.  Если a = 0, то такое разложение называется рядом Маклорена:

Теорема 1 (необходимое условие разложимости функции в степенной ряд). Если функция  раскладывается в степенной ряд (Тейлора), то она имеет непрерывные производные всех порядков внутри интервала сходимости.  

{Степенной ряд  можно почленно дифференцировать произвольное число раз.   При этом непосредственной подстановкой получаем: 

Таким образом, разложение функции в степенной ряд является рядом Тейлора этой функции,

в коэффициенты которого входят производные всех порядков}

Следствие. Разложение функции в степенной ряд единственно.

Замечание. Условие не является достаточным:

функция 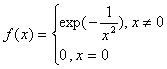   имеет все  производные в нуле равными нулю:

 Остальные производные вычисляются аналогично. Ряд Маклорена имеет вид:   0 + 0х +0х² + … = 0 ≠ 

  Теорема 2 (необходимое и достаточное условие разложимости). Бесконечно дифференцируемая

на интервале сходимости функция раскладывается в ряд Тейлора тогда и только тогда, когда остаточный член в формуле Тейлора 

{ По формуле Тейлора:

}

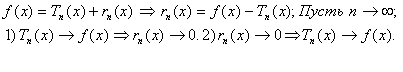  Следствие.  Для разложимости  в степенной ряд бесконечно дифференцируемой на интервале сходимости функции достаточно, чтобы все ее производные были ограничены одним числом.

{  }

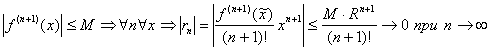№36. Разложение в ряды Маклорена основных элементарных функций.

Разложение некоторых функций в ряд Маклорена











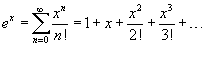
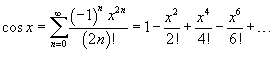
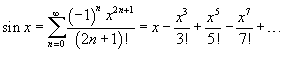
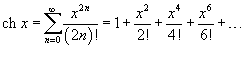
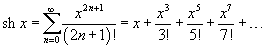
№38. Комплексные ряды. Сходящиеся, абсолютно сходящиеся и условно сходящиеся ряды. Формулы Эйлера.