
- •2. . Он называется сходящимся, если существует конечный предел частичного интервала . В противном случае он расходящийся.
- •14.Достаточные условия экстремума функции многих переменных с использованием второго дифференциала и критерия Сильвестра.
- •15. Определение двойного интеграла
- •1.2. Основные свойства двойного интеграла
- •1.4. Геометрическая трактовка двойного интеграла
- •20. Интегрируемые типы уравнений первого порядка
- •Однородные дифференциальные уравнения
- •Линейные дифференциальные уравнения первого порядка
- •Дифференциальные уравнения в полных дифференциалах. Интегрирующий множитель
- •Дифференциальные уравнения первого порядка, не разрешённые относительно производной .
- •24 Метод вариации произвольных постоянных
- •Остаточные признаки сходимости знакоположительного ряда.
- •Сходящиеся, абсолютно сходящиеся и условно сходящиеся комплексные ряды
- •Функции комплексной переменной как суммы абсолютно сходящихся степенных рядов. Формула Эйлера
24 Метод вариации произвольных постоянных
Рассмотрим
ЛНДУ (5.1). Его общим решением является
функция (5.3), т. е.![]()
Частное
решение![]() уравнения
(5.1) можно найти, если известно общее
решение
уравнения
(5.1) можно найти, если известно общее
решение![]() соответствующего
однородного уравнения (5.2), методом
вариации произвольных постоянных (метод
Лагранжа), состоящим в следующем. Пусть
соответствующего
однородного уравнения (5.2), методом
вариации произвольных постоянных (метод
Лагранжа), состоящим в следующем. Пусть![]() -
общее решение уравнения (5.2).Заменим в
общем решении постоянные c1 и
с2 неизвестными
функциями c1(x)
и с2(х)
и подберем их так, чтобы функция
-
общее решение уравнения (5.2).Заменим в
общем решении постоянные c1 и
с2 неизвестными
функциями c1(x)
и с2(х)
и подберем их так, чтобы функция
![]()
была решением уравнения (5.1). Найдем производную
![]()
Подберем функции c1(x) и с2(х) так, чтобы
![]()
Тогда
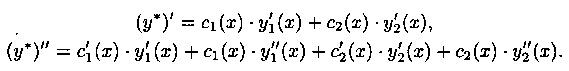
Подставляя
выражение для ![]() в
уравнение (5.1), получим:
в
уравнение (5.1), получим:
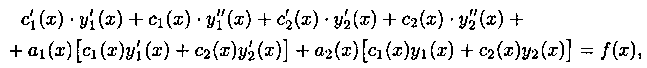
или
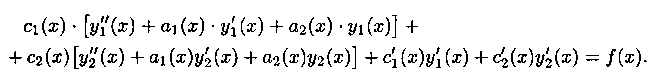
Поскольку y1(x) и у2(х) - решения уравнения (5.2), то выражения в квадратных скобках равны нулю, а потому
![]()
Таким образом, функция (5.6) будет частным решением у* уравнения (5.1), если функции c1(x) и с2(х) удовлетворяют системе уравнений (5.7) и (5.8):
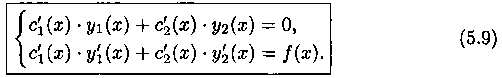
Определитель
системытак как это определитель Вронского
для фундаментальной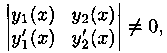 системы
частных решений у1 (х)
и у2 (х)
уравнения (5.2). Поэтому система (5.9) имеет
единственное решение: с'1(х)= j1(x)
и с'2(х)=j2(х),
где j1(x)
и j2(х)
- некоторые функции от х. Интегрируя эти
функции, находим c1(x)
и с2(х),
а затем по формуле (5.6) составляем частное
решение уравнения (5.1).
системы
частных решений у1 (х)
и у2 (х)
уравнения (5.2). Поэтому система (5.9) имеет
единственное решение: с'1(х)= j1(x)
и с'2(х)=j2(х),
где j1(x)
и j2(х)
- некоторые функции от х. Интегрируя эти
функции, находим c1(x)
и с2(х),
а затем по формуле (5.6) составляем частное
решение уравнения (5.1).
Метод подбора

№25. Некоторые понятия, связанные с системами дифференциальных уравнений, и постановка задачи Коши для нормальной системы дифференциальных уравнений. Линейные уравнения дифференциальных уравнений. Векторно-матричная форма записи. Связь между линейными системами и дифференциальными уравнениями.
Рассмотрим систему дифференциальных уравнений y'1 = f1(x, y1, y2 , ..., yn), y'2 = f2 (x, y1, y2 , ..., yn), .............................. y'n = fn (x, y1, y2 , ..., yn), где x — независимая переменная, а y1(x), y2(x), ..., yn(x) — неизвестные функции, n — порядок системы.
Обозначив
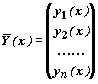
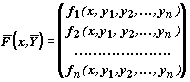 запишем
систему в векторной форме
Y '=F(x,Y ).
запишем
систему в векторной форме
Y '=F(x,Y ).
Решением системы называется вектор-функция Y , которая определена и нерерывно дифференцируема на интервале (a, b) и удовлетворяет системе, т.е. для всех x0 (a, b) справедливо Y '(x) =F(x,Y (x)).
Задачей Коши (задачей с начальными условиями) называется следующая задача: найти такое решениеY (x) системы Y '=F(x,Y ), что Y (x0) =Y 0, где x0 — заданное число, а Y 0 — заданный вектор.
Интегральной кривой системы называется кривая в (n+1) -мерном пространстве Rn+1x,y, заданная уравнением Y =Y (x), где Y (x) - решение системы.Таким образом, решить задачу Коши — это значит найти интегральную кривую, проходящую через заданную точку пространства Rn+1x,y.
Для нормальных систем обыкновенных дифференциальных уравнений справедлива следующая теорема существования и единственности решения задачи Коши.
Если вектор-функция F(x,Y (x)) и ее частные производные по переменным yi , i = 1, 2, ...,n, непрерывны в области G пространства Rn+1x,y, то на некотором интервале (x0 -h, x0+h) существует единственное решение системы Y '(x) =F(x,Y (x)) , удовлетворяющее начальному условию Y (x0) =Y 0, т.е. через каждую точку области G проходит единственная интегральная кривая системы.
Подробнее геометрическая интерпретация систем обыкновенных дифференциальных уравнений и их решений рассмотрена в разделе, посвященном изучению автономных систем.
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
![]()
где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
Использование интегрирующего множителя;
Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
![]()
Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение диффференциального уравнения выражается в виде:
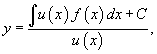
где C − произвольная постоянная.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
![]()
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме y(x0) = y0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y(x0) = y0.
№26. Линейные однородные системы дифференциальных уравнений (ЛОСУ) и свойства их решений.
Линейные однородные системы дифференциальных уравнений
Простейшая однородная
система дифференциальных уравнений
имеет следующий вид:
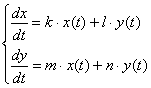
Собственно, почти все практические примеры такой системой и ограничиваются =)
Что тут есть?
![]() –
это числа (числовые коэффициенты). Самые
обычные числа. В частности, один, несколько
или даже все коэффициенты могут быть
нулевыми. Но такие подарки подкидывают
редко, поэтому числа
чаще
всего не равны нулю.
–
это числа (числовые коэффициенты). Самые
обычные числа. В частности, один, несколько
или даже все коэффициенты могут быть
нулевыми. Но такие подарки подкидывают
редко, поэтому числа
чаще
всего не равны нулю.
![]() и
и ![]() –
это неизвестные функции. В качестве
независимой переменной выступает
переменная
–
это неизвестные функции. В качестве
независимой переменной выступает
переменная ![]() –
это «как бы икс в обычном дифференциальном
уравнении».
–
это «как бы икс в обычном дифференциальном
уравнении».
![]() и
и ![]() –
первые производные неизвестных
функций
и
соответственно.
–
первые производные неизвестных
функций
и
соответственно.
Что значит решить систему дифференциальных уравнений?
Это значит, найти такие функции и , которые удовлетворяют и первому и второму уравнению системы. Как видите, принцип очень похож на обычные системы линейных уравнений. Только там корнями являются числа, а здесь – функции.
Найденный ответ записывают
в виде общего решения
системы дифференциальных уравнений:
![]()
Для системы ДУ можно решить задачу Коши, то есть, найти частное решение системы, удовлетворяющее заданным начальным условиям. Частное решение системы тоже записывают с фигурными скобками.
Более
компактно систему можно переписать
так:
![]()
Но в
ходу традиционно более распространен
вариант решения с производными,
расписанными в дифференциалах, поэтому,
пожалуйста, сразу привыкайте к следующим
обозначениям:
и
–
производные первого порядка;
![]() и
и ![]() –
производные второго порядка.
–
производные второго порядка.
№27. Фундаментальная система решений (ФСР) ЛОСУ. Теорема об общем решении ЛОСУ.
Для линейного однородного дифференциального уравнения n-го порядка
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = 0,
где y = y(x) — неизвестная функция, a1(x), a2(x), ..., an-1(x), an(x) — известные, непрерывные, справедливо: 1) существуют n линейно независимых решений уравнения y1(x), y2(x), ..., yn(x); 2) при любых значениях констант c1, c2, ..., cn функция y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) является решением уравнения; 3) для любых начальных значений x0, y0, y0,1, ..., y0,n-1 существуют такие значения c*1,c*n, ..., c*n, что решение y*(x)=c*1 y1(x) + c*2 y2(x) + ... + c*n yn (x) удовлетворяет при x = x0 начальным условиям y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
Выражение y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) называется общим решением линейного однородного дифференциального уравнения n-го порядка.
Совокупность n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка y1(x), y2(x), ..., yn(x) называется фундаментальной системой решений уравнения.
№28. Решение ЛОСУ с постоянными коэффициентами методом Эйлера.
Линейная однородная система дифференциальных уравнений с постоянными коэффициентами
![]()
![]()
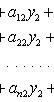
![]()
![]()
В векторной форме:
dY/dx = AY,
где
![]()
![]()
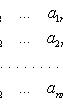
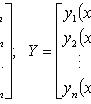
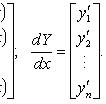
Характеристическое уравнение
![]()
![]()
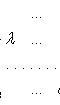
![]()
![]()
или ![]()
![]() .
.
Нахождение общего решения системы по методу Эйлера
1. Если ![]()
![]() -
простой корень характеристического
уравнения, то ему соответствует решение
-
простой корень характеристического
уравнения, то ему соответствует решение
![]()
![]()
![]()
![]()
![]()
числа ![]()
![]() находятся
из системы
находятся
из системы
![]()
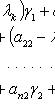
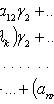
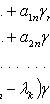
![]()
2. Если - корень кратности m характеристического уравнения, то ему соответствует решение вида
![]()
![]()
![]()
![]()
![]()
где P1(x), P2(x), ..., Pn(x) - многочлены степени не выше m-1, имеющие в совокупности m произвольных постоянных.
Коэффициенты многочленов можно определить, подставив выражения для y1, y2, ..., yn в исходную систему.
Найдя решения, соответствующие каждому корню характеристического уравнения, общее решение системы получим как линейную комбинацию этих решений.
Например, если все корни характеристического уравнения простые, а решениями, соответствующими этим корням , будут:
![]()
![]()
![]()
![]()
![]()
то общее решение этой системы имеет вид:
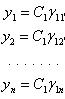
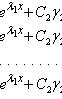
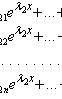
![]()
![]()
№29. Теорема об общем решении линейной неоднородной системы дифференциальных уравнений (ЛНСУ).
Для линейного неоднородного дифференциального уравнения n-го порядка
y(n) + a1(x) y(n-1) + ... + an-1 (x) y' + an(x) y = f(x),
где y = y(x) — неизвестная функция, a1(x), a2(x), ..., an-1(x), an(x), f(x) — известные, непрерывные, справедливо: 1) если y1(x) и y2(x) — два решения неоднородного уравнения, то функция y(x) = y1(x) - y2(x) — решение соответствующего однородного уравнения; 2) если y1(x) решение неоднородного уравнения, а y2(x) — решение соответствующего однородного уравнения, то функция y(x) = y1(x) + y2(x) — решение неоднородного уравнения; 3) если y1(x), y2(x), ..., yn(x) — n линейно независимых решений однородного уравнения, а yч(x) — произвольное решение неоднородного уравнения, то для любых начальных значений x0, y0, y0,1, ..., y0,n-1 существуют такие значения c*1, c*n, ..., c*n, что решение y*(x)=c*1 y1(x) + c*2 y2(x) + ... + c*n yn (x) + yч(x) удовлетворяет при x = x0 начальным условиям y*(x0)=y0, (y*)'(x0)=y0,1 , ...,(y*)(n-1)(x0)=y0,n-1.
Выражение y(x)= c1 y1(x) + c2 y2(x) + ... + cn yn(x) + yч(x) называется общим решением линейного неоднородного дифференциального уравнения n-го порядка.
№30. Числовые ряды. Основные определения. Общие свойства рядов. Необходимые признаки сходимости рядов.
Основные определения и понятия.
Пусть
мы имеем числовую последовательность ![]() ,
где
,
где ![]() .
Приведем
пример числовой последовательности:
.
Приведем
пример числовой последовательности: ![]() .
Числовой
ряд – это сумма
членов числовой последовательности
вида
.
Числовой
ряд – это сумма
членов числовой последовательности
вида ![]() .
В
качестве примера числового ряда можно
привести сумму бесконечно убывающей
геометрической прогрессии со знаменателем q
= -0.5:
.
В
качестве примера числового ряда можно
привести сумму бесконечно убывающей
геометрической прогрессии со знаменателем q
= -0.5: 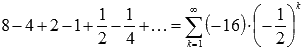 .
.
![]() называют общим
членом числового ряда или k–ым членом
ряда.
Для предыдущего примера
общий член числового ряда имеет
вид
называют общим
членом числового ряда или k–ым членом
ряда.
Для предыдущего примера
общий член числового ряда имеет
вид 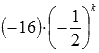 .
Частичная
сумма числового ряда –
это сумма вида
.
Частичная
сумма числового ряда –
это сумма вида ![]() ,
где n –
некоторое натуральное число.
,
где n –
некоторое натуральное число. ![]() называют
также n-ой частичной
суммой числового ряда.
К примеру,
четвертая частичная сумма
ряда
называют
также n-ой частичной
суммой числового ряда.
К примеру,
четвертая частичная сумма
ряда 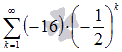 есть
есть ![]() .
Частичные
суммы
.
Частичные
суммы ![]() образуют
бесконечную последовательность частичных
сумм числового ряда.
Для нашего
ряда n –ая частичная
сумма находится по формуле суммы
первых n членов
геометрической прогрессии
образуют
бесконечную последовательность частичных
сумм числового ряда.
Для нашего
ряда n –ая частичная
сумма находится по формуле суммы
первых n членов
геометрической прогрессии 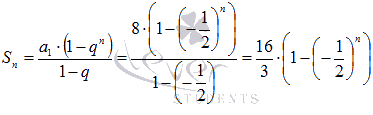 ,
то есть, будем иметь следующую
последовательность частичных
сумм:
,
то есть, будем иметь следующую
последовательность частичных
сумм: 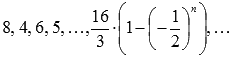 .
Числовой
ряд
.
Числовой
ряд ![]() называется сходящимся,
если существует конечный предел
последовательности частичных сумм
называется сходящимся,
если существует конечный предел
последовательности частичных сумм ![]() .
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется расходящимся.
Суммой
сходящегося числового ряда
называется
предел последовательности его частичных
сумм, то есть,
.
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется расходящимся.
Суммой
сходящегося числового ряда
называется
предел последовательности его частичных
сумм, то есть, ![]() .
В
нашем примере
.
В
нашем примере 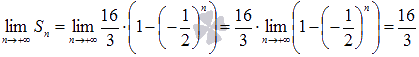 ,
следовательно, ряд
сходится,
причем его сумма равна шестнадцати
третьим:
,
следовательно, ряд
сходится,
причем его сумма равна шестнадцати
третьим: 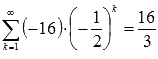 .
В
качестве примера расходящегося ряда
можно привести сумму геометрической
прогрессии со знаменателем большем,
чем единица:
.
В
качестве примера расходящегося ряда
можно привести сумму геометрической
прогрессии со знаменателем большем,
чем единица: 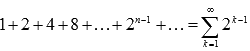 . n–ая частичная
сумма определяется выражением
. n–ая частичная
сумма определяется выражением 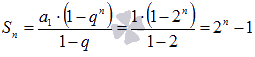 ,
а предел частичных сумм бесконечен:
,
а предел частичных сумм бесконечен: ![]() .
Еще
одним примером расходящегося числового
ряда является сумма вида
.
Еще
одним примером расходящегося числового
ряда является сумма вида ![]() .
В этом случае n–аячастичная
сумма может быть вычислена как
.
В этом случае n–аячастичная
сумма может быть вычислена как ![]() .
Предел частичных сумм бесконечен
.
Предел частичных сумм бесконечен ![]() .
Сумма
вида
.
Сумма
вида ![]() называется гармоническим
числовым рядом.
Сумма
вида
называется гармоническим
числовым рядом.
Сумма
вида 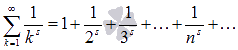 ,
где s –
некоторое действительное число,
называетсяобобщенно
гармоническим числовым рядом.
Приведенных
определений достаточно для обоснования
следующих очень часто используемых
утверждений, рекомендуем их запомнить.
,
где s –
некоторое действительное число,
называетсяобобщенно
гармоническим числовым рядом.
Приведенных
определений достаточно для обоснования
следующих очень часто используемых
утверждений, рекомендуем их запомнить.
ГАРМОНИЧЕСКИЙ РЯД
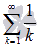 ЯВЛЯЕТСЯ
РАСХОДЯЩИМСЯ.
Докажем расходимость
гармонического ряда.
Предположим,
что ряд сходится. Тогда существует
конечный предел его частичных сумм. В
этом случае можно записать
ЯВЛЯЕТСЯ
РАСХОДЯЩИМСЯ.
Докажем расходимость
гармонического ряда.
Предположим,
что ряд сходится. Тогда существует
конечный предел его частичных сумм. В
этом случае можно записать 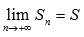 и
и 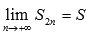 ,
что приводит нас к равенству
,
что приводит нас к равенству 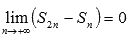 .
С
другой стороны,
.
С
другой стороны,
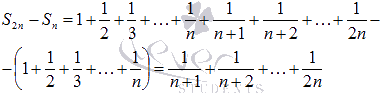 Не
вызывают сомнения следующие неравенства
Не
вызывают сомнения следующие неравенства 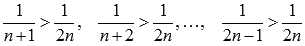 .
Таким образом,
.
Таким образом, 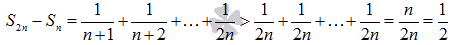 .
Полученное неравенство
.
Полученное неравенство 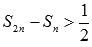 указывает
нам на то, что равенство
не
может быть достигнуто, что противоречит
нашему предположению о сходимости
гармонического ряда.
Вывод:
гармонический ряд расходится.
указывает
нам на то, что равенство
не
может быть достигнуто, что противоречит
нашему предположению о сходимости
гармонического ряда.
Вывод:
гармонический ряд расходится.
СУММА ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ВИДА
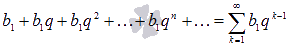 СО
ЗНАМЕНАТЕЛЕМq ЯВЛЯЕТСЯ
СХОДЯЩИМСЯ ЧИСЛОВЫМ РЯДОМ, ЕСЛИ
СО
ЗНАМЕНАТЕЛЕМq ЯВЛЯЕТСЯ
СХОДЯЩИМСЯ ЧИСЛОВЫМ РЯДОМ, ЕСЛИ 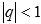 ,
И РАСХОДЯЩИМСЯ РЯДОМ ПРИ
,
И РАСХОДЯЩИМСЯ РЯДОМ ПРИ 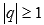 .
Докажем
это.
Мы знаем, что сумма
первых n членов
геометрической прогрессии находится
по формуле
.
Докажем
это.
Мы знаем, что сумма
первых n членов
геометрической прогрессии находится
по формуле 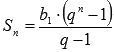 .
При
справедливо
.
При
справедливо
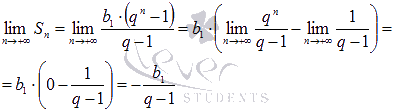 что
указывает на сходимость числового
ряда.
При q =
1 имеем числовой
ряд
что
указывает на сходимость числового
ряда.
При q =
1 имеем числовой
ряд 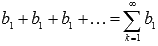 .
Его частичные суммы находятся как
.
Его частичные суммы находятся как 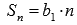 ,
а предел частичных сумм бесконечен
,
а предел частичных сумм бесконечен  ,
что указывает на расходимость ряда в
этом случае.
Если q
= -1, то числовой ряд
примет вид
,
что указывает на расходимость ряда в
этом случае.
Если q
= -1, то числовой ряд
примет вид 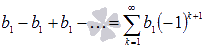 .
Частичные суммы принимают значение
.
Частичные суммы принимают значение 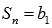 для
нечетных n,
и
для
нечетных n,
и 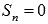 для
четных n.
Из этого можно сделать вывод, что предел
частичных сумм не существует и ряд
расходится.
При
для
четных n.
Из этого можно сделать вывод, что предел
частичных сумм не существует и ряд
расходится.
При 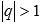 справедливо
справедливо
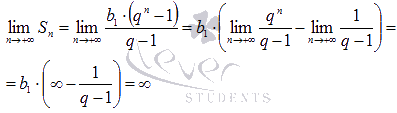 что
указывает на расходимость числового
ряда.
что
указывает на расходимость числового
ряда.
ОБОБЩЕННО ГАРМОНИЧЕСКИЙ РЯД
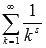 СХОДИТСЯ
ПРИ s > 1 И
РАСХОДИТСЯ ПРИ
СХОДИТСЯ
ПРИ s > 1 И
РАСХОДИТСЯ ПРИ 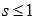 .
Доказательство.
Для s
= 1 получим
гармонический ряд
,
а выше мы установили его расходимость.
При s
< 1 справедливо
неравенство
.
Доказательство.
Для s
= 1 получим
гармонический ряд
,
а выше мы установили его расходимость.
При s
< 1 справедливо
неравенство 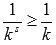 для
всех натуральных k.
В силу расходимости гармонического
ряда
можно
утверждать, что последовательность
его частичных сумм неограниченна (так
как не существует конечного предела).
Тогда последовательность частичных
сумм числового ряда
тем
более неограниченна (каждый член этого
ряда больше соответствующего члена
гармонического ряда), следовательно,
обобщенно гармонический ряд расходится
при s < 1.
Осталось
доказать сходимость ряда
при s
> 1.
Запишем
разность
для
всех натуральных k.
В силу расходимости гармонического
ряда
можно
утверждать, что последовательность
его частичных сумм неограниченна (так
как не существует конечного предела).
Тогда последовательность частичных
сумм числового ряда
тем
более неограниченна (каждый член этого
ряда больше соответствующего члена
гармонического ряда), следовательно,
обобщенно гармонический ряд расходится
при s < 1.
Осталось
доказать сходимость ряда
при s
> 1.
Запишем
разность 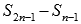 :
:
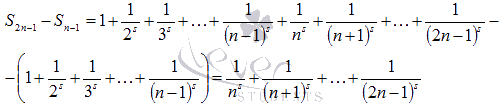 Очевидно,
что
Очевидно,
что 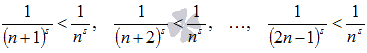 ,
тогда
,
тогда
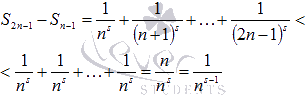 Распишем
полученное неравенство для n
= 2, 4, 8, 16, …
Распишем
полученное неравенство для n
= 2, 4, 8, 16, …
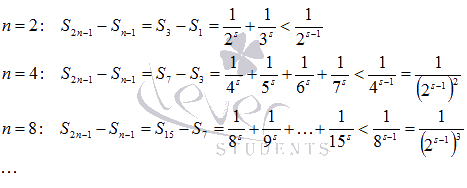 Используя
эти результаты, с исходным числовым
рядом можно провести следующие
действия:
Используя
эти результаты, с исходным числовым
рядом можно провести следующие
действия:
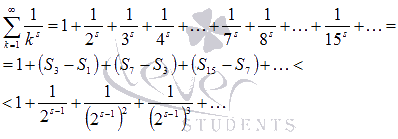 Выражение
Выражение 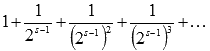 представляет
собой сумму геометрической прогрессии,
знаменатель которой равен
представляет
собой сумму геометрической прогрессии,
знаменатель которой равен 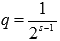 .
Так как мы рассматриваем случай при s
> 1, то
.
Так как мы рассматриваем случай при s
> 1, то 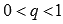 .
Поэтому
.
Поэтому 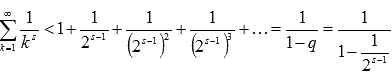 .
Таким образом, последовательность
частичных сумм обобщенно гармонического
ряда при s >
1 является
возрастающей и в тоже время ограниченной
сверху значением
.
Таким образом, последовательность
частичных сумм обобщенно гармонического
ряда при s >
1 является
возрастающей и в тоже время ограниченной
сверху значением 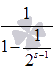 ,
следовательно, она имеет предел, что
указывает на сходимость ряда
.
Доказательство завершено.
,
следовательно, она имеет предел, что
указывает на сходимость ряда
.
Доказательство завершено.
Числовой
ряд
называется знакоположительным,
если все его члены положительны, то
есть, ![]() .
Числовой
ряд
.
Числовой
ряд ![]() называется знакочередующимся,
если знаки его соседних членов различны.
Знакочередующийся числовой ряд можно
записать в виде
называется знакочередующимся,
если знаки его соседних членов различны.
Знакочередующийся числовой ряд можно
записать в виде ![]() или
или ![]() ,
где
.
Числовой
ряд
называется знакопеременным,
если он содержит бесконечное множество
как положительных, так и отрицательных
членов.
Знакочередующийся числовой
ряд является частным случаем
знакопеременного ряда.
Ряды
,
где
.
Числовой
ряд
называется знакопеременным,
если он содержит бесконечное множество
как положительных, так и отрицательных
членов.
Знакочередующийся числовой
ряд является частным случаем
знакопеременного ряда.
Ряды
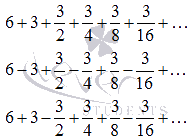 являются
знакоположительным, знакочередующимся
и знакопеременным соответственно.
Для
знакопеременного ряда существует
понятие абсолютной и условной
сходимости.
Знакопеременный
ряд
называется абсолютно
сходящимся, если
сходится ряд из абсолютных величин его
членов, то есть, сходится знакоположительный
числовой ряд
являются
знакоположительным, знакочередующимся
и знакопеременным соответственно.
Для
знакопеременного ряда существует
понятие абсолютной и условной
сходимости.
Знакопеременный
ряд
называется абсолютно
сходящимся, если
сходится ряд из абсолютных величин его
членов, то есть, сходится знакоположительный
числовой ряд ![]() .
К
примеру, числовые ряды
.
К
примеру, числовые ряды ![]() и
и ![]() абсолютно
сходятся, так как сходится ряд
абсолютно
сходятся, так как сходится ряд ![]() ,
являющийся суммой бесконечно убывающей
геометрической прогрессии.
Знакопеременный
ряд
называется условно
сходящимся, если
ряд
расходится,
а ряд
сходится.
В
качестве примера условно сходящегося
числового ряда можно привести ряд
,
являющийся суммой бесконечно убывающей
геометрической прогрессии.
Знакопеременный
ряд
называется условно
сходящимся, если
ряд
расходится,
а ряд
сходится.
В
качестве примера условно сходящегося
числового ряда можно привести ряд 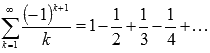 .
Числовой ряд
.
Числовой ряд 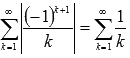 ,
составленный из абсолютных величин
членов исходного ряда, расходящийся,
так как является гармоническим. В то же
время, исходный ряд является сходящимся,
что легко устанавливается с помощью признака
Лейбница. Таким
образом, числовой знакочередующийся
ряд
условно
сходящийся.
,
составленный из абсолютных величин
членов исходного ряда, расходящийся,
так как является гармоническим. В то же
время, исходный ряд является сходящимся,
что легко устанавливается с помощью признака
Лейбница. Таким
образом, числовой знакочередующийся
ряд
условно
сходящийся.
Свойства сходящихся числовых рядов.
Если сходится числовой ряд , то сходящимся будет и ряд
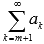 .
Другими словами, сходящимся будет и
ряд без первых m членов.
Если к сходящемуся числовому
ряду
добавить
несколько членов (от первого до m-ого),
то полученный ряд также будет сходящимся.
.
Другими словами, сходящимся будет и
ряд без первых m членов.
Если к сходящемуся числовому
ряду
добавить
несколько членов (от первого до m-ого),
то полученный ряд также будет сходящимся.
Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд
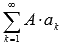 ,
причем
,
причем 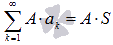 ,
где A –
произвольная постоянная.
,
где A –
произвольная постоянная.
