
вопрос
А, В,Z –обозначения множеств
а , b , z – элементы множеств
операции над множествами: 1.объединение 2.пересечения 3. Разность.
Функция ,пусть даны некоторые множества Х и У Ф-называет закон\правило ,по которому каждому элементу х из Х поставлен в однозначное соответствие элемент у из У .х- область определений функции у-область значений функции.
Виды функций:
Функция называется сюръекцией если для у и ф(х)существует у=ф(х).
Функция называется инъекцией , если она взаимно однозначна , т.е если ф(х1)=ф(х2) то х1=х2
Функция называться биекция если она одновременно сюръекция и инъекция.
Вопрос
Основные числовые множества .
Натуральные числа N=(1,2,3,4…..бесконечности)- складываются перемножаются вычитаться не всегда.
Целые числа Z=(-inf….-2,-1,0,1,2…+Inf)- складываться , перемножаются , вычитаются. деление не всегда
Рациональные числа Q=(p/q) p.q принадлежат z(q-не равно 0)-выполняются все 4 алгебраические операции кроме деления на 0.
Множество действительных чисел –R множество всевозможных десятичных дробей(конечных и бесконечных) выполняется все 4 алгебраические операции.
Множество на прямой

Свойство непрерывности – каждой точке на прямой соответствуют какие-то числа.
Аксиома непрерывности
Пусть дана система вложенных отрезков(а1,b1)>(a2b2)>…(an, bn)
Тогда пересечение всех этих отрезков не пусто (иметься хотя бы одна точка).
3 Вопрос.
Последовательность назеваться функция f: N->R ,f(n)-значения последовательности, на значение аргумента n или Fn –n-ый член последовательности (Fn,n=1,2,3….)
Виды последовательностей
Ограниченные сверху
Ограниченные снизу
Ограниченные (ограничены и сверху и снизу одновременно)
Не ограниченные.
Монотонно возрастающие(убывающая).(каждый последующий член больше (меньше )предыдущего)
Сходящаяся последовательность (имеющая конечны предел)
Последовательность
(Fn) имеющая конечны предел
а (а принадлежит R )
Бесконечно большая последовательность
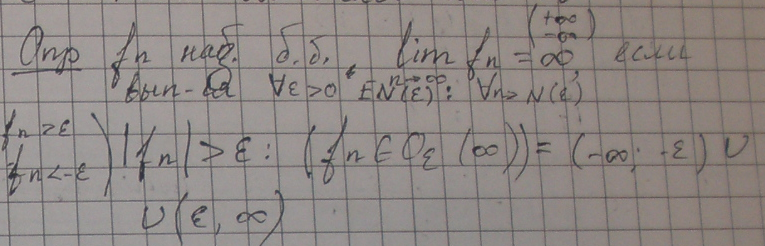
Теоремы о пределах
Предел сходящей последовательности является единственным(определи однозначно)
Сходящаяся последовательность ограничена
Арифметические свойства пределов (при условие что lima и limb существуют):
Lim(a+-b)=lima+-limb ;lim(a*b)=lima*limb;lim(a/b)=lima/limb(b не= 0)
4.
5. Монотонная возрастающая последовательность ограниченная сверху(снизу) имет конечный предел(сходиться).
Вопрос 4.
Первый замечательный предел:
![]()
Второй замечательный предел:
![]()
Раскрытие неопределённости с помощью Лопиталя , эквивалентно малых , домножением на сопряжённое выражение, с помощью бинома ньютона.

Вопрос 5
Точка а называется пределом функции F: X->R в точке х0 если для любой последовательности xn принадлежит Х n=1.2.3….., имеющая свои пределом точку х0 , т.е такая что lim,n->inf,xn=x0 последовательность {f(xn)} имеет своим пределом точку а lim,n->inf,f(xn)=a
Предел
по Гейне :
Значение ![]() называется пределом (предельным
значением)
функции
называется пределом (предельным
значением)
функции ![]() в
точке
в
точке ![]() ,
если для любой последовательноститочек
,
если для любой последовательноститочек ![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции ![]() сходится
к
.[1]
сходится
к
.[1]
![]()
Предел
по Каши: Значение
называется пределом (предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа ε найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
такое,
что для всех аргументов ![]() ,
удовлетворяющих условию
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .[1]
.[1]
![]()
Определения по каши и Гейне эквивалентны.
Для того чтобы функцияf:X->R имела конечный предел или определенного знака бесконечный предел т . х0 необходима и достаточно , чтобы для любой последовательности хn->x0,xn принадлежит X ,n=1,2,3….последовательность соответствующих значений функции имела конечный или определённого знака бесконечный предел.
Если предел существует то он единственен .
Б.М функции . Функция a: X->R называется бесконечно малой при х->x0 ,если Lim(a(x))=0.
6 Вопрос
Арифметические свойства пределов
Lim(a+-b)=lima+-limb ;lim(a*b)=lima*limb;lim(a/b)=lima/limb(b не= 0)
Первый замечательный предел:
Второй замечательный предел:
7 Вопрос
Непрерывность функций : Функция f:X->R называется непрерывной в точке x0принодлежит Х если lim,x->x0,f(x)=f(x0)
Свойства
Функция, непрерывная в точке
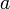 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки.
Если функция
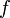 непрерывна
в точке
и
непрерывна
в точке
и 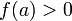 (или
(или 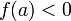 ),
то
),
то  (или
(или 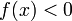 )
для всех
,
достаточно близких к
.
)
для всех
,
достаточно близких к
.Если функции и
 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции 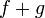 и
и 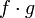 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
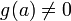 ,
то функция
,
то функция 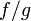 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.8 вопрос . Переход к пределу под знак непрерывной функции .
Если сложна функция F(f(x)) определена в некоторой точке х0 и не прерывна в ней то
Lim,x->x0,F(f(x))=F(f(x0))=F(lim,x->x0,f(x))p;
