20. Интегрируемые типы уравнений первого порядка

 Интегрируемые типы дифференциальных уравнений первого порядка 

Рассмотрим уравнение первого порядка, разрешенное относительно первой производной:

y'=f(x,y); x'=q(x,y),                 (2.1)

где неизвестной является функция y(x) (либо x(y)), а известной является функция f(x,y) (либо q(x,y)). Учитывая, что , а  , и полагая возможным представить f(x,y) или q(x,y) в виде -  , уравнение (2.1) можно записать в симметричной форме

P(x,y)dx+Q(x,y)dy=0 (2.2)

Если в этом уравнении P(x,y) и Q(x,y) можно представить в виде P(x,y)=N(x)R(y) и Q(x,y)=M(x)K(y), то уравнение (2.2) записывается как

N(x)R(y)dx+M(x)K(y)dy=0               (2.3)

Это уравнение называется уравнением с разделяющимися переменными. Метод его решения: разделив (2.3) на произведение M(x)K(y) получим

                     (2.4)

Уравнение (2.4) называется уравнением с разделенными переменными. Операция деления уравнения (2.3) на произведение М(х)R(y) называется разделением переменных. Интегрируя (2.4), получим общий интеграл

исходного уравнения. При делении (2.3) на произведение М(х)R(y), можно потерять некоторые решения, которые получаются из уравнения

М(х)R(y)=0

Определяя из этого уравнения решения y= (x), следует проверить, является ли оно решением уравнения (2.3). Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл. Если входит, то оно есть частное решение, а если не входит, то это решение называется особым.

Однородные дифференциальные уравнения

Дифференциальное уравнение   называется однородным, если   – однородная функция нулевой степени. Дифференциальное уравнение первого порядка в симметричной форме  является однородным, если   – однородные функции одной степени.  Замена   приводит однородное уравнение к уравнению с разделяющимися переменными. Пример  Решить уравнение  . Найти решение, удовлетворяющее начальному условию  .  Данное уравнение однородное. Произведя замену  , получим 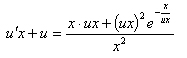 (здесь мы учли, что  ). Сокращаем на  . Учитывая, что  , получим 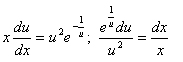 . Интегрируем полученное равенство: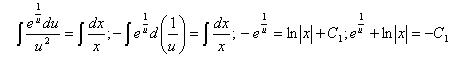 . Обозначая  и учитывая  , получаем ответ  . Для данного начального условия  :  . Следовательно, искомое частное решение есть .

Линейные дифференциальные уравнения первого порядка

Дифференциальные уравнения вида   называются линейными. Существуют несколько методов их решения: метод Бернулли, метод Лагранжа, метод интегрирующего множителя. Метод Бернулли Решение уравнения   ищется в виде  . При этой замене получаем:  Функцию   выбирают из условия  . Полученную функцию   подставляют в уравнение   (учитываем ), решая которое находят функцию  .  Пример Решить уравнение  .  Полагая   и учитывая  , получим  . Преобразуем полученное уравнение:  . Функцию   выберем из условия u`+ 2xu = 0. Учитывая  , получаем  . Интегрируем это равенство:   ( см. примечание).  Подставляя полученный результат   в уравнение  , и учитывая, что при  , получим  . Сократим последнее равенство на  и учтем  . Учитывая  , ответ будет таким: .  Примечание При интегрировании равенства  , получается результат  , откуда следует, что   или  . Однако в методе Бернулли нас интересует не все множество функций  , а лишь одна функция из этого множества. Проще всего принять   и выбрать  , тогда  .

 

Уравнением Бернулли называется уравнение первого порядка вида

Здесь a(x) и b(x) — известные, непрерывные на [a;b] функции, n > 1.

Заменой z(x) =  y^1-n(x) уравнение Бернулли сводится к линейному уравнению относительно функции z(x):

Получили линейное относительно z(x) уравнение: