1. Теорема о связи первообразных одной и той же функции. Определение неопределенного интеграла.
Первообразной функции f(x) на некотором (конечном или бесконечном) интервале называется дифференцируемая функция F(х), производная которой равна f(x) во всех точках интервала, т.е. F'(х) = f(x).
Тоерем. Любые 2 постоянные функции отличаются не постоянностью. Если g(x) др. первообразн. f(x), то g(x)=f(x)+сб где с-const. Док-во: По услов. F’(x)=f(x), G’(x)=g(x) Рассмотр. Функ-ию, найдем ее производн. G’(x)-F’(x) = g(x) – f(x)=0 =>
G’(x)-F’(x) =с, т.е G’(x)= F’(x) +с. Вывод: Множество всех первообразных ф-ий f(x) устроено так: нужно взять одну из первообр. И к ней прибавлять всевозможные постоянные.
Неопределённым
интегралом
функции
f(x)
называется
множество всех её первообразных. Сл-но
где F(х) — одна из первообразных, а С — произвольная постоянная.
Для проверки формулы (1) достаточно найти производную функции F(х) и убедиться в том, что она равна подынтегральной функции f(х).
Отыскание неопределённого интеграла называется интегрированием функции. Будет доказано, что любая непрерывная функция имеет первообразную. Однако интеграл элементарной функции может не быть элементарной функцией (такие интегралы называются "неберущимися").
2. Взаимная обратность операций интегрирования и дифференцирования. Свойство линейности неопределенного интеграла.
Интегрирование и дифференцирование есть две взаимно обратные операции. Всякому правилу дифференцирования соответствует правило (метод) интегрирования. Так, свойство линейности производной переходит в свойство линейности интеграла. Правилу дифференцирования сложной функции соответствует, как мы видели, метод интегрирования введением под знак дифференциала. Этому же правилу соответствует также метод интегрирования заменой переменной. И правилу дифференцирования произведения соответствует метод интегрирования по частям.
Свойство линейности: интеграл от линейной комбинации функций равен линейной комбинации от интегралов этих функций.
3. Задачи о вычислении площади криволинейной трапеции и нахождении длины пути по известной скорости.
Вычисление площадей криволинейных трапеций. Из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, то есть области, лежащей под графиком функции у = f(х),
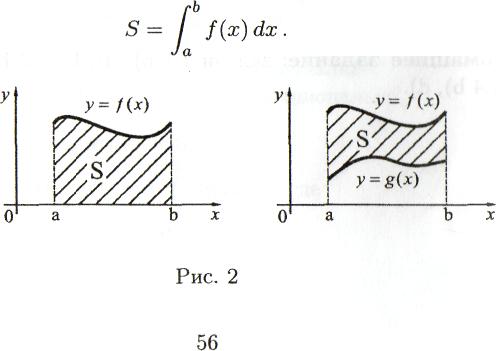f(х)
>
О, вычисляется по формуле
Площадь
области D,
расположенной между графиками двух
функций, т.е. D
: а ≤ х ≤ b,
g(х)
≤ у ≤ f(х),
вычисляется
по формуле
Пусть время движения изменяется от t0 до Т. При равномерном движении пройденный путь равен произведению скорости v на время движения (Т- t0), т.е. S=v(Т-t0), v=const.
В случае неравномерного движения эта формула непригодна. Разобьем интервал [t0,Т] на ряд частичных интервалов Dti. При малых Dti, скорость
изменится незначительно и на каждом частичном интервале ее приближенно можно считать постоянной. Вычислим на каждом частичном интервале скорость, и найдем величину пройденного пути.
Значение величины пути будет вычислено тем точнее, чем меньше частичные интервалы времени Dti. Точное значение получим как предел суммы, т. е;
В правой части равенства находится предел интегральной суммы функции v(t) на - интервале [t0,T], равный соответствующему определенному интегралу.