2. Правило свертки. Правило является следствием второго распределительного закона. Запись правила:

Доказательство. К левой части выражения применяется второй распределительный закон, т.е.

Первая скобка правой части равна единице (см. тождественное соотно­шение 4), поэтому Также доказывается равенство

3. Правило расширения. Правило записывается в следующем виде:

Понятие расширения объясняется возможностью добавления к правой части конъюнкции 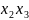. Справедливость правила доказывается искусствен­ным приемом. Конъюнкция умножается на дизъюнкцию

затем делаются простые преобразования, т.е.

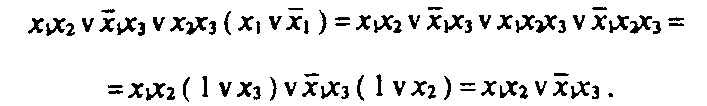
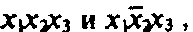
3. Правило склеивания. Правило склеивания базируется на понятии соседних конъюнкций. Соседними называются конъюнкции, отличающиеся представлением одной переменной. Например, конъюнкции 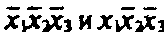являются попарно соседними. В первой паре конъюнкции отли­чаются представлением , а во второй — представлением По этим переменным конъюнкции склеиваются. Формулировка правила: две сосед-

10.

ние конъюнкции склеиваются с образованием одной конъюнкции меньшего ранга; исчезает та переменная, по которой конъюнкции склеиваются. Пример Задана логическая функция в СДНФ

Необходимо упростить функцию. Так как конъюнкции функции сосед­ние и отличаются представлением то путем их склеивания получаем

Справедливость преобразования (склеивания) доказывается вынесе­нием общих переменных в конъюнкциях за скобку, т.е.

ТИПОВЫЕ ЗАДАЧИ ПО ПРЕОБРАЗОВАНИЮ ЛОГИЧЕСКИХ ФУНКЦИЙ

Задачи по преобразованию логических функций весьма разнообразны. Однако их можно подразделить на следующие типовые группы:

1. Упрощение логических функций, заданных различным образом;

2. Построение таблиц истинности функций;

3. Вычисление значения логического выражения для заданного набора значений переменных;

4. Определение тождественности логических функций.

5. Построение функциональной схемы узла, реализующего заданную логическую функцию.

Упрощение логических функций, заданных различным образом

1. Функция задана в произвольной форме.

Пример 1. Упростить логическую функцию, заданную выражением:

а) приведение функции к ДНФ путем использования законов и правил, т.е.

а) приведение функции к ДНФ путем использования законов и правил, т.е.

б ) вычеркивание конъюнкции равных нулю.

Конъюнкция конъюнкции равны нулю, поэтому

получаем упрощенную функцию

Пример 2. Упростить логическую функцию, заданную выражением:

а) применение закона отрицания с целью последующего перехода к ДНФ, т.е.

11.

б) анализ промежуточного результата. Устанавливаем, что первая скобка равна единице, так как где. Окончательно получаем

Пример 3. Упростить логическую функцию, заданную выражением:

а) упрощение функции путем использования закона отрицания и пере­множения скобок

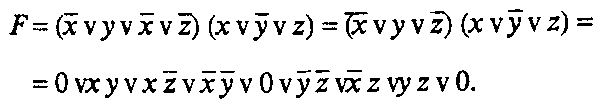
б) применение правила расширения:

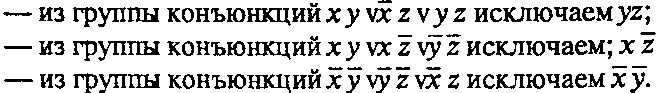
Окончательно получаем:

Покажем, что если применять другую последовательность исключения лишних конъюнкций, можно получить другой вид функции, которая не под­дается дальнейшему упрощению.

Применяем правило расширения в следующей последовательности:

В результате получаем:

Эта функция по рассмотренным правилам и законам упрощению не поддается.

Заметим, что если имеется несколько форм одной функции, не подда­ющихся дальнейшим упрощениям, то они называются тупиковыми. Одна из них является минимальной.

2. Функция задана таблицей истинности.

Пример 4. Упростить функцию F (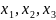 ) равную единице на наборах 3, 5,6,7 (011,101,110,111).

а) построение таблицы истинности (рис. 2.9 а).

В первых трех столбцах записываются возможные наборы. В столбце F на наборах 011,101,110 и 111 проставляются единицы; на остальных наборах проставляются нули.

12.

б) запись функции в СДНФ (см. правило записи). Наборам 011,101,110,111 соответствуют конъюнкции

поэтому функция будет записана в следующем виде: в) упрощение функции.

функции, записанные в СДНФ, первоначально упрощаются по правилу склеивания. Затем применяются другие правила и тождественные соотноше­ния.

В данной функции первые три конъюнкции являются соседними с чет­вертой. Функция не изменится, если к ней подписать еще две конъюнкции

После склеивания пар соседних конъюнкций окончательно получим:

Можно было не подписывать конъюнкцию , а просто склеить поочередно три первые конъюнкции с четвертой конъюнкцией.

Построение таблиц истинности функций Пример 5. Построить таблицу истинности функции:

а) запись заданной функции в СДНФ.

Данная функция зависит от трех переменных и записана в ДНФ. Для записи функции в СДНФ первая конъюнкция умножается на выражение , а вторая — на выражение В скобках используются тепеременные и их отрицания, которые отсутствуют в конъюнкциях:

б) определение наборов, на которых функция принимает единичное значение.

Так как по правилу записи конъюнкций в СДНФ единице в наборе соответствует переменная, а нулю — ее отрицание, то конъюнкциям соответствуют наборы 111,110,011,001, т.е. 7,6, 3,1.

в) непосредственное построение таблицы.

В столбце F таблицы (рис. 2.9 б) на наборах 111, 110, 011, 001 проставляются единицы, а на остальных наборах ставятся нули.

Вычисление значения логического выражения для заданного набора значении переменных

Для вычисления значения логического выражения на заданном наборе значений переменных можно применять два способа: способ использования СДНФ и способ подстановки. Рассмотрим первый из них.

13.

Пример 6. Вычислить значение логического выражения

т.е. на наборе 6, или 110.

а) получение СДНФ заданной функции (см. выше пример 4):

После исключения повторяющейся конъюнкции получим:

б) определение значения выражения.

Выражение V принимает единичное значение только на наборах 100, ООО и 101, или 4, 0, 5 т.к. задан набор 6, то логическое выражение принимает нулевое значение (V = 0).

Второй способ не нуждается в особых пояснениях. При заданных значе­ниях x=1,y=lиz-0 имеем у = 0, z = 1. Подставляем эти значения в выражение и получаем: V= 0•1v 1 • 0 = 0 v 0 = 0.

В случае вычисления значений сложных логических выражений второй способ не исключает ошибок.

Определение тождественности логических функций

Тождественными являются те логические функции, которые имеют оди­наковые СДНФ, т.е. одинаковые таблицы истинности. Поэтому при опреде­лении тождественности для логических функций должны быть построены таблицы истинности или получены СДНФ. Таблицы или СДНФ сравнивают­ся и делается вывод о тождественности функций.

Пример 7. Проверить тождественность логических функций:

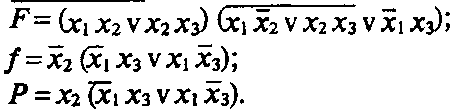
а) упрощение функции F.

Применяем закон отрицания и перемножаем скобки, т. е.

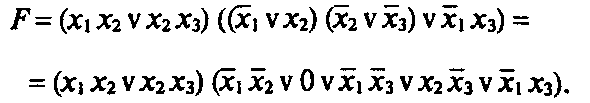
Во второй скобке конъюнкции склеиваются, поэтому получаем

Переменная поглощает конъюнкцию что дает

или

14.

функция F оказалась записанной в СДНФ, так как содержит конъюнкции одинакового ранга и в них входят все переменные, от которых она Зависит.

б) преобразование функции f.

функция f также записана в СДНФ.

Так как СДНФ функций F и f не совпадают, то они не являются тождественными,

в) преобразование функции Р.

Получена СДНФ функции Р.

Функции F и Р являются тождественными, так как имеют одинаковые СДНФ.

Пример 8. Проверить тождественность логических функций:

которая принимает единичные значения на наборах 2,3. а) упрощение функции F. Применяется закон отрицания

Во второй скобке переменная поглощает конъюнкцию , что при водит к следующему результату

Во второй скобке используется правило свертки и затем скобки перемножаются:

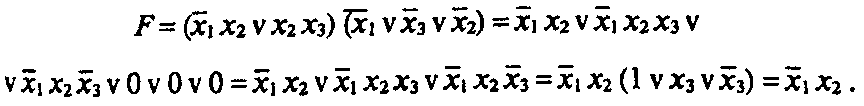
б) получение СДНФ функции F.

в) получение СДНФ функции f.

Так как функция f принимает единичные значения на наборах 2 и 3. тп СДНФ будет иметь вид

15.

Функции F и f имеют одинаковые СДНФ, следовательно они то ценны.

Пример9. Проверить тождественность логических функций:

Функция f имеет следующую минимальную форму

а) упрощение функции f; — перемножение скобок;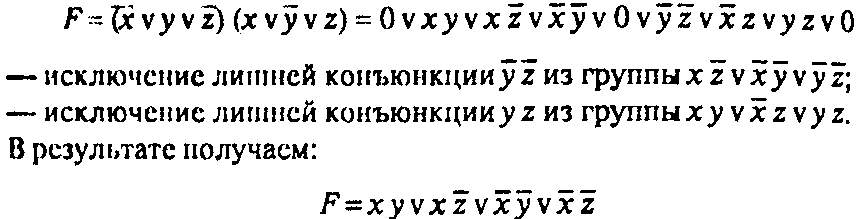

Упрощенная форма функции F и минимальная форма функции f не совпадают. Однако это не значит, что функции не тождественны. Для окон­чательногопынода нужно получить СДНФ обеих функций.

б) получение СДНФ функции F.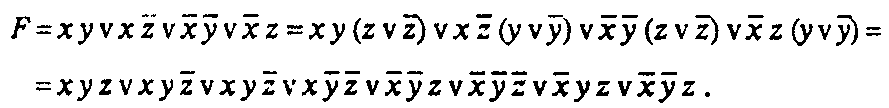

После удаления повторяющихся конъюнкций получаем:

в) получение СДНФ функции f:

Функции F и f имеют одинаковые СДНФ и принимают единичные значе­ния на одних и тех же наборах 0,1,3,4,6,7. Эти функции тождественны. Так как минимальные формы функций не совпадают, то можно сделать вывод, что для функции F была получена тупиковая форма.