
- •Билет № 1
- •2. Теорема о решении однородной системы линейных уравнений.
- •Билет № 2
- •2. Необходимые и достаточные условия разрешимости транспортной задачи линейного программирования.
- •Билет № 3
- •2. Базис системы векторов. Теорема о единственности разложения вектора по базису.
- •Билет № 4
- •2. Теорема об улучшении опорного решения задачи линейного программирования, её следствия (признак оптимальности опорного решения).
- •Билет № 5
- •2. Теорема об оптимальности опорного решения задачи линейного программирования с искусственными переменными.
- •Билет № 6
- •2. Теоремы об отсутствии оптимального решения задачи линейного программирования с искусственными переменными.
- •Билет № 7
- •2. Теорема об экстремуме целевой функции задачи линейного программирования.
- •Билет № 8
- •2. Первая теорема двойственности.
- •Билет № 9
- •2. Вторая теорема двойственности.
- •Билет № 10
- •2. Построение начального опорного решения задачи линейного программирования и переход от одного опорного решения к другому.
- •Ответы к задачам
Билет № 9
2. Вторая теорема двойственности.
Теорема 5.2. Для того, чтобы допустимые
решения
![]() ,
,
![]() являлись оптимальными решениями пары
двойственных задач, необходимо и
достаточно, чтобы выполнялись следующие
равенства
являлись оптимальными решениями пары
двойственных задач, необходимо и
достаточно, чтобы выполнялись следующие
равенства
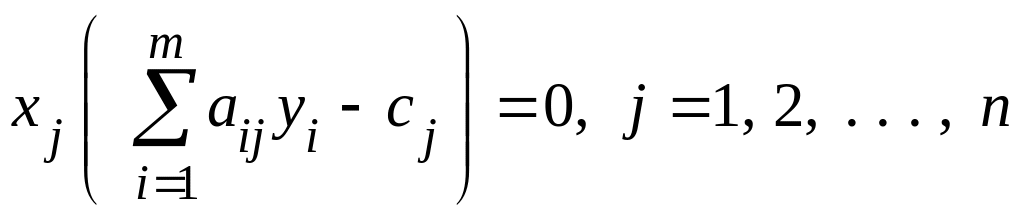 ;
(5.22)
;
(5.22)
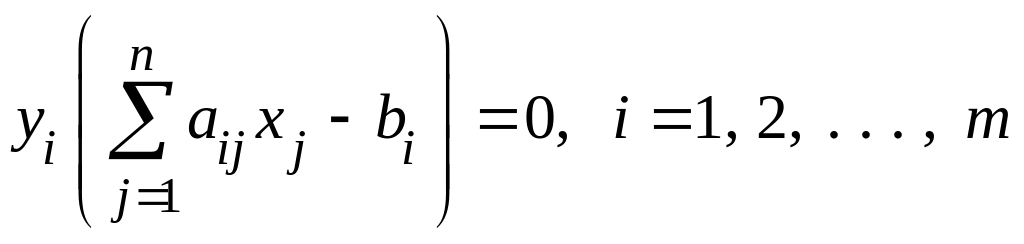 .
(5.23)
.
(5.23)
Иначе, если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи выполняется как строгое неравенство, то i-я координата оптимального решения двойственной задачи равна нулю и, наоборот, если i-я координата оптимального решения двойственной задачи отлична от нуля, то i-е ограничение исходной задачи удовлетворяется оптимальным решением как равенство.
Д о к а з а т е л ь с т в о. Необходимость. Пусть и оптимальные решения пары двойственных задач (5.21).
1. Покажем, что в этом случае выполняются равенства (5.22).
Подставим оптимальные решения X,
Y в системы ограничений
своих задач, получим
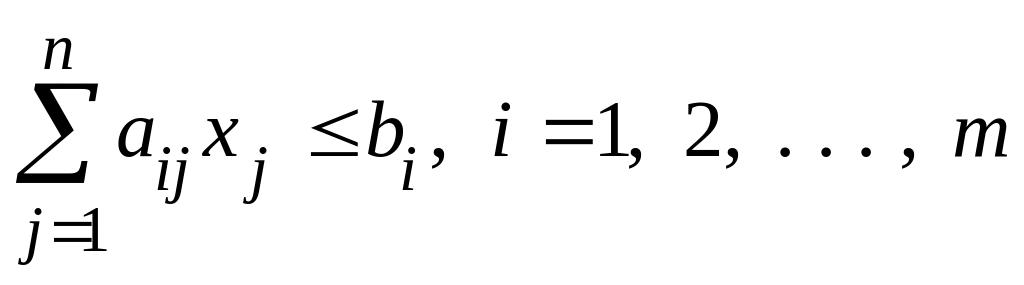 ;
;
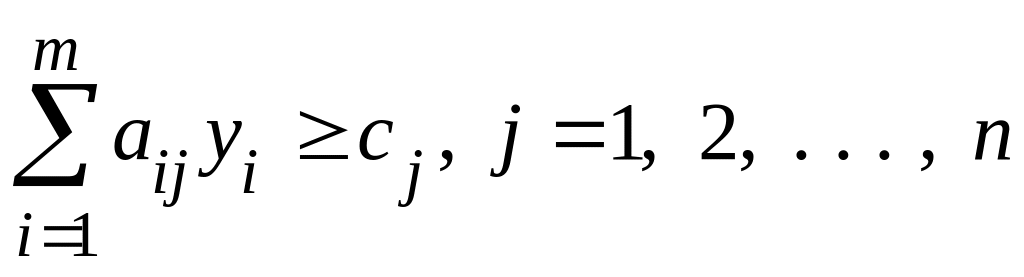 .
.
Затем каждое из тождеств умножим на соответствующую переменную двойственной задачи и после этого просуммируем их, получим
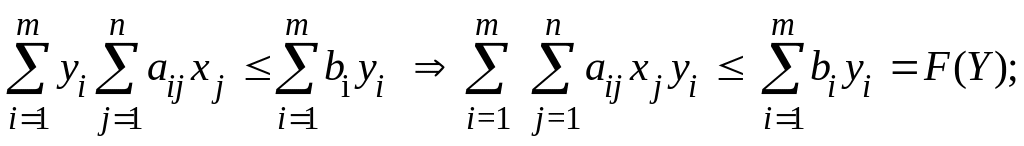
 .
.
Отсюда следует
 .
.
Так как X, Y оптимальные решения, то по первой теореме двойственности Z(X) = F(Y). Поэтому заменим в последнем соотношении знаки "" на "=", получим
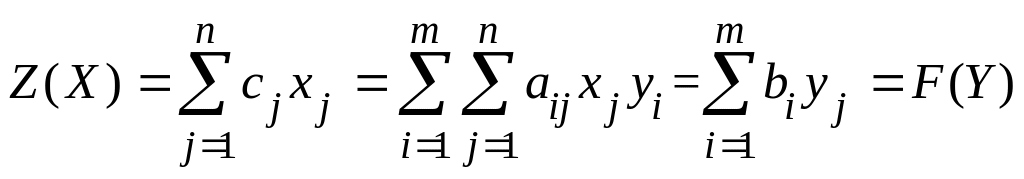 .
(5.24)
.
(5.24)
Отсюда можно записать
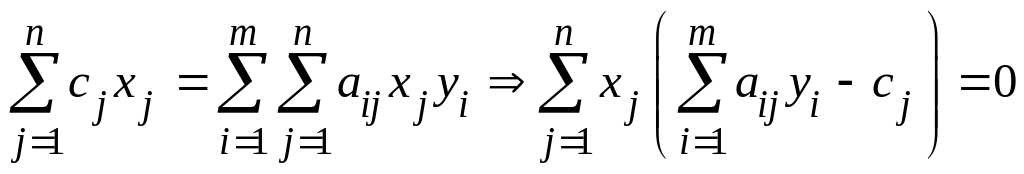 .
.
Учитывая,
что
![]() и
,
а следовательно и
и
,
а следовательно и
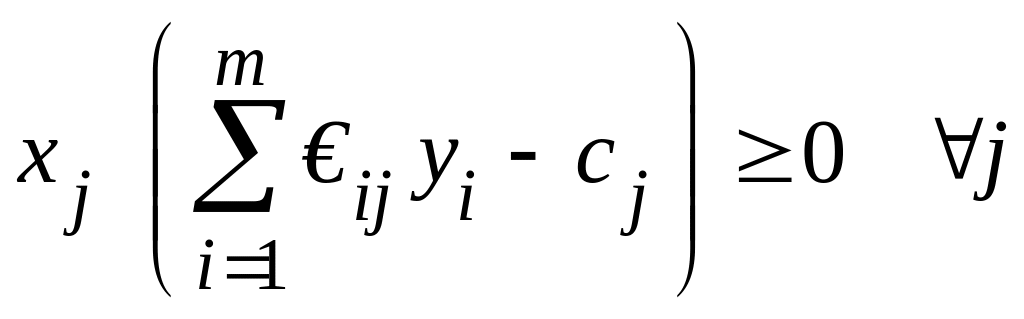 ,
приходим к выводу, что каждое слагаемое
суммы равно нулю, т.е. справедливы
равенства (5.22)
,
приходим к выводу, что каждое слагаемое
суммы равно нулю, т.е. справедливы
равенства (5.22)
 .
.
2. Аналогично докажем справедливость
равенств (5.23). Используя выражения
(5.24), запишем
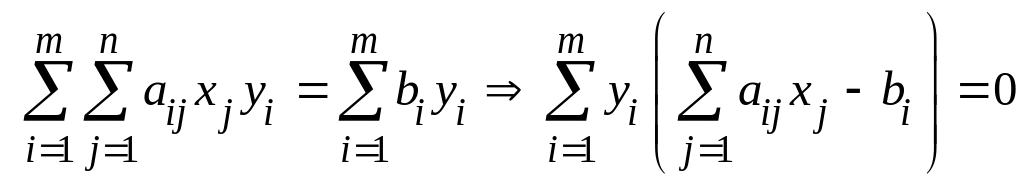 .
.
Учитывая, что
![]() и
,
делаем вывод, что каждое слагаемое
суммы равно нулю, т.е.
и
,
делаем вывод, что каждое слагаемое
суммы равно нулю, т.е.
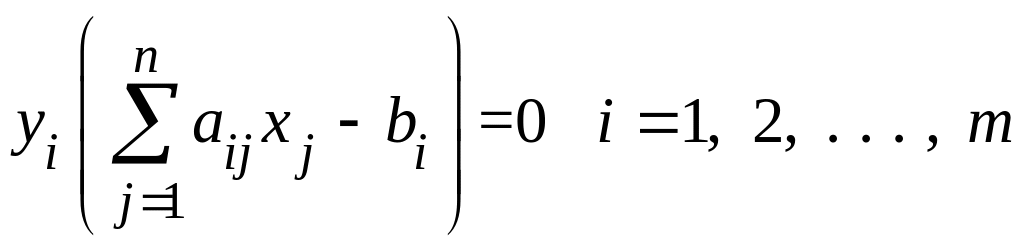 .
.
Необходимость доказана.
Достаточность. Пусть равенства (5.22), (5.23) выполняются. Докажем, что в этом случае и являются оптимальными решениями.
Просуммируем каждую группу данных равенств, получим
 ;
;
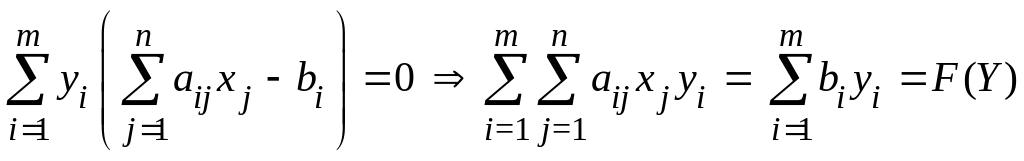 .
.
Из данных равенств следует, что Z(X) = F(Y). Из первой теоремы двойственности (теорема 5.1) следует, что значения целевых функций пары двойственных задач равны только на оптимальных решениях. Поэтому можно утверждать, что X и Y являются оптимальными решениями. Теорема доказана полностью.
Билет № 10
2. Построение начального опорного решения задачи линейного программирования и переход от одного опорного решения к другому.
Получим правило выбора разрешающих элементов для преобразований Жордана, обеспечивающее сохранение неотрицательности правых частей системы уравнений.
Пусть
разрешающим элементом для преобразования
Жордана является коэффициент
![]() при неизвестной
при неизвестной
![]() в уравнении с номером l.
В результате преобразования Жордана
правые части уравнений, как известно,
пересчитываются по следующим формулам:
в уравнении с номером l.
В результате преобразования Жордана
правые части уравнений, как известно,
пересчитываются по следующим формулам:
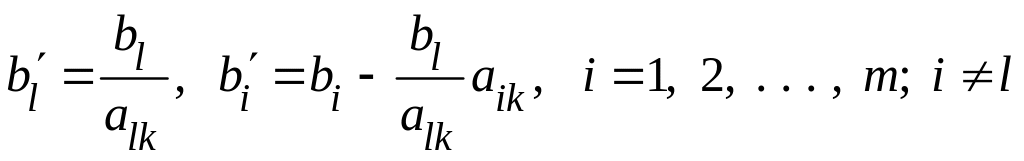 .
.
1. Для того,
чтобы правая часть
![]() уравнения с разрешающим элементом
уравнения с разрешающим элементом
![]() оставалась неотрицательной, должно
выполняться неравенство
оставалась неотрицательной, должно
выполняться неравенство
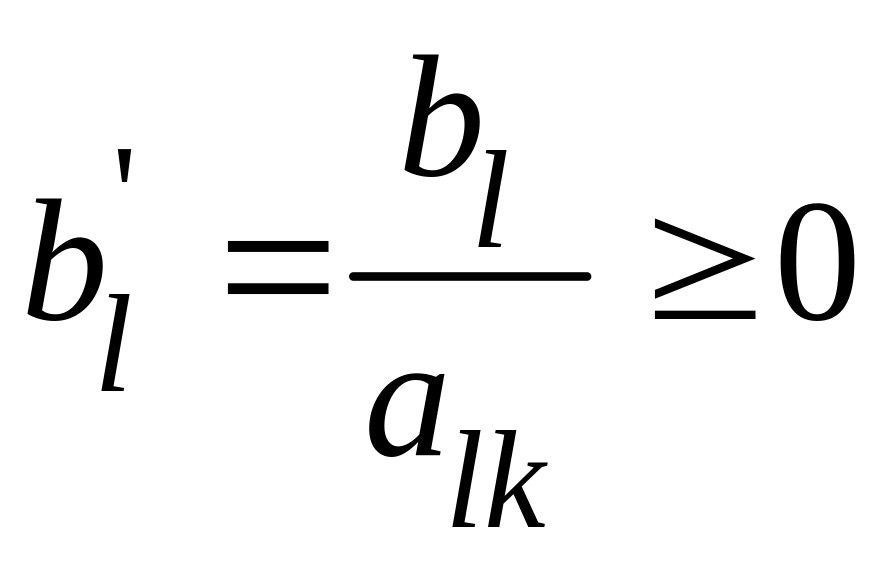 .
.
Так как
![]() ,
то первое условие для разрешающего
элемента
состоит в том, что он должен быть
положительным, т.е.
,
то первое условие для разрешающего
элемента
состоит в том, что он должен быть
положительным, т.е.
![]() .
.
2. Неотрицательными также должны быть правые части остальных уравнений, т. е.
 .
.
Для получения
требований, налагаемых на разрешающий
элемент
![]() ,
рассмотрим два случая:
,
рассмотрим два случая:
а) если
![]() ,
то ввиду того, что
,
то ввиду того, что
![]() ,
,
,
без дополнительных условий имеем
,
,
,
без дополнительных условий имеем
![]() ;
;
б) если же
![]() ,
то неравенство
,
то неравенство
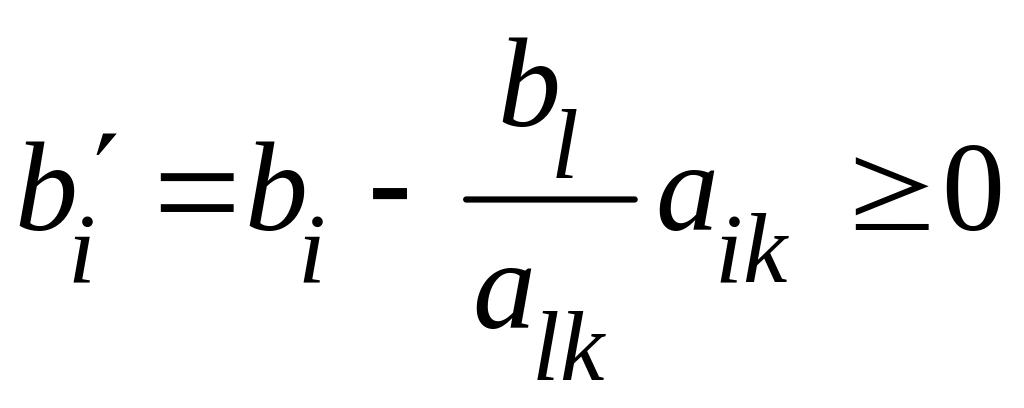 поделим на
поделим на
![]() ,
получим
,
получим
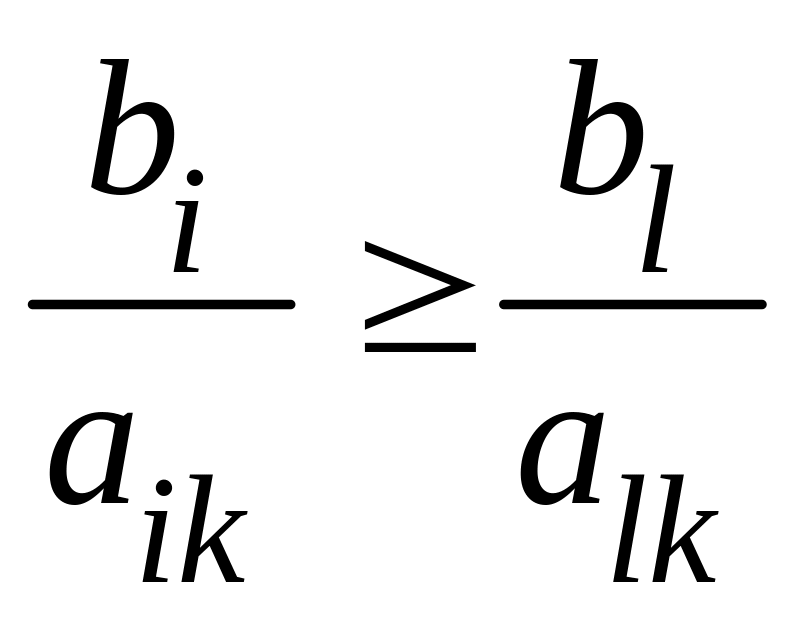 .
.
Данное неравенство должно выполняться для любого уравнения с номером i, в котором . Для удобства вычислений вводят вспомогательный параметр
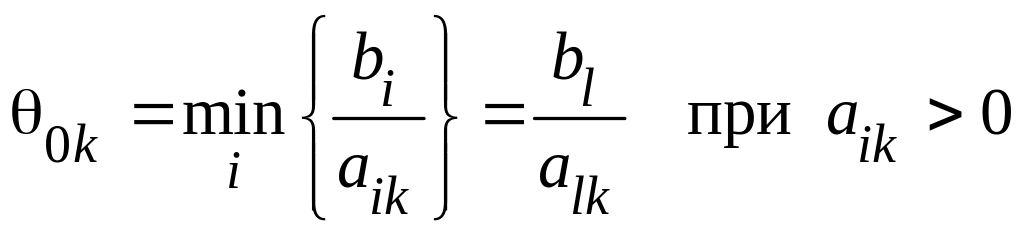 .
(4.4)
.
(4.4)
Здесь k
номер вектора
условия
,
вводимого в базис (выбираемого столбца
матрицы системы ограничений), а l
номер вектора
![]() ,
выводимого из базиса (номер строки
матрицы, в которой должен выбираться
разрешающий элемент для преобразования
Жордана).
,
выводимого из базиса (номер строки
матрицы, в которой должен выбираться
разрешающий элемент для преобразования
Жордана).
С помощью данного условия возможно выбрать разрешающий элемент в любом столбце k матрицы системы ограничений, в котором имеется хотя бы один положительный элемент. При нарушении данного условия выбора разрешающего элемента в правой части системы уравнений появляются отрицательные величины.
Используя данное условие, можно найти начальное опорное решение.
Аналогичное условие может быть использовано при переходе от одного опорного решения к другому.
Пусть система уравнений-ограничений с помощью подходящего выбора разрешающих элементов приведена к равносильной разрешённой так, что правые части системы сохранились неотрицательными, и имеет вид
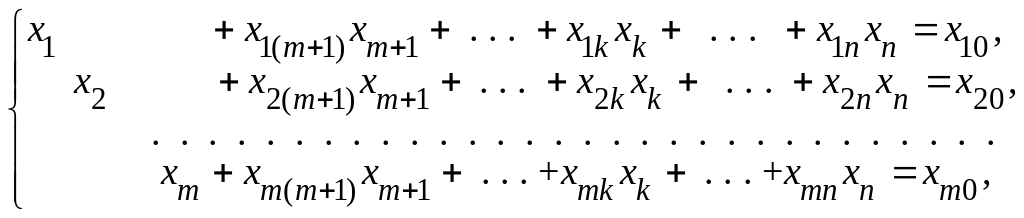
.
Тогда базисное
решение
![]() является допустимым и опорным решением
с базисом из единичных векторов
является допустимым и опорным решением
с базисом из единичных векторов
![]() .
.
Очевидно, для перехода
от этого опорного решения к новому
необходимо использовать соотношение
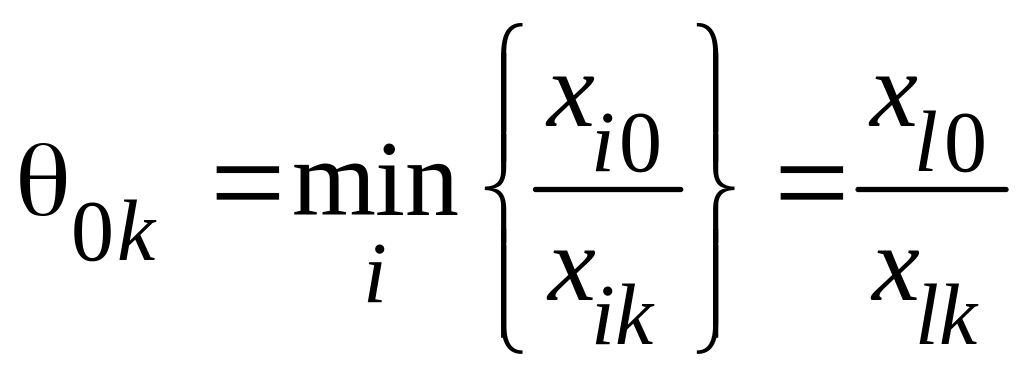 при
при
![]() ,
(4.5)
,
(4.5)
где k
номер вектора,
вводимого в базис, l
номер вектора,
выводимого из базиса,
![]() координаты опорного
решения,
координаты опорного
решения,
![]() коэффициенты
разложения вектора
коэффициенты
разложения вектора
![]() по базису опорного решения.
по базису опорного решения.
