Численное вычисление одномерных интегралов

Рассмотрим определенный интеграл вида

. (7.13)

Для большинства подынтегральных функций f(x) вычислить аналитически данный интеграл не удается, и поэтому интеграл (7.13) нужно вычислять численно.

Классический метод численного интегрирования основан на геометрической интерпретации интеграла (7.13) как площади под графиком функции f(x) в пределах от x=a до x=b (рис.7.3).

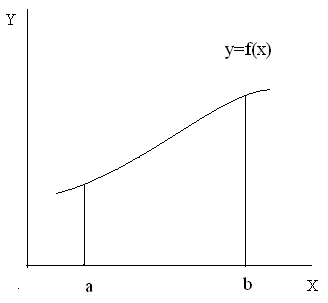
Рис. 7.3

Делим отрезок (a,b) на n равных отрезков x:

. (7.14)

Тогда x₀=a, x_i=x_i+ix, x_к=x_n (7.15)

Простейшей оценкой площади под кривой f(x) служит сумма площадей прямоугольников (рис.7.4).

Рис. 7.4

В методе прямоугольников значение функции f(x) вычисляется в начале каждого отрезка (в точке слева), и оценка интеграла дается выражением

. (7.16)

Модификацией метода прямоугольников является вычисление f(x) в средней точке каждого отрезка:

. (7.17)

Другим приближением является формула трапеций, в которой интеграл оценивается вычислением площади трапеции со сторонами, равными значениям f(x) в начале и конце отрезка.

S трапеции = (f(x₀)+ f(x₀+dx))/2.

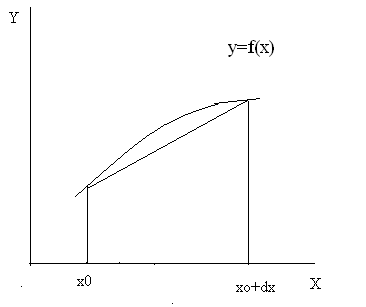
Рис. 7.5

Оценка интеграла дается выражением

. (7.18)

Очевидно, что точность вычисления интегралов вышеописанными методами определяется шагом сетки x: чем меньше его величина, тем с большей точностью мы вычисляем интеграл.

Задание

Вычислите любым из описанных выше методов интеграл

и сравните приближенный ответ с точным значением интеграла.

Метод Монте-Карло

Метод Монте-Карло является весьма популярным методом в математическом моделировании физических задач и основывается на проведении серии статистических испытаний. Метод Монте-Карло является самостоятельным методом и не относится к числу методов раздела математики, называемого “Численные методы”.

Проиллюстрируем метод на примере следующей задачи. Каким образом можно измерить площадь озера, имея только кучу камней? Предположим, что озеро расположено на поле известной площади S.

Если бросать камни произвольным образом в пределы озера, то часть камней попадет в озеро. Тогда площадь озера приблизительно равна площади поля, умноженной на долю камней, попавших в озеро. Если n – количество брошенных камней, а m – количество камней, попавших в озеро, то площадь озера будет определяться формулой S озера = S*m /n.

Рис. 6.6

Рассмотрим данный метод применительно к вычислению определенного интеграла.

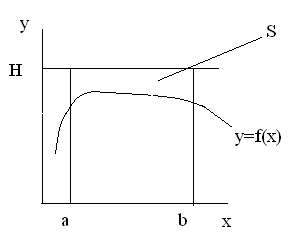
S=H(b-a)

Рис. 6.7

Площадь прямоугольника, ограниченного линиями y=H, y=0, x=a, x=b, равна S. Площадь под кривой y=f(x) на интервале (a,b) равна F.

Будем генерировать n пар случайных чисел x_i, y_i (I=1, 2,…n), таких, что:

A x_i b, 0 y_i H. (7.19)

Доля m пар точек (x_i,y_i), которые удовлетворяют условию

y_i f(x_i), (7.20)

представляют собой отношение интеграла F к площади прямоугольника S.

Отсюда оценка интеграла методом Монте-Карло определяется выражением

, (7.21)

где F_n=H(b-a)*m/n, m – доля точек, удовлетворяющих условию (7.20); n – общее количество сгенерированных пар точек (x_i,y_i), удовлетворяющих условию (7.19).

Другая разновидность метода Монте-Карло основывается на теореме, гласящей, что оценка определенного интеграла определяется следующей формулой:

  f  *(b-a), (7.22)

где  f  – среднее значение функции f(x) на интервале (a,b).

Для вычисления  f  будем генерировать случайные числа x_i, удовлетворяющие условию a  x_i  b, и вычислять значения функции f(x_i) в этих точках. Тогда оценка одномерного интеграла будет иметь вид

 F_n= f  (b-a)= (b-a)*1/n (7.23)

где x_i – случайные числа; n – число испытаний.

Данный метод называется методом выборочного среднего.

Рассмотрим вопрос точности вычисления интегралов методом Монте-Карло. Понятно, что чем больше случайных точек мы сгенерируем, тем точнее будет оценка интеграла, причем можно показать, что точное значение интеграла F лежит в некотором интервале с центром в точке F_n:

F(F_n-_n, F_n+_n).

Здесь _n=/n,

где  – это дисперсия; n – число испытаний.

Дисперсия  определяется по формулам:

²= f ² -  f ², (7.24)

 f  = , (7.24а)

 f ² = . (7.24б)