
Произвольная усечённая пирамида
Формулы для усечённой пирамиды
Объём пирамиды ![]() ,
где
,
где ![]() —
площади оснований,
—
высота усечённой пирамиды.
—
площади оснований,
—
высота усечённой пирамиды.
Площадь боковой
поверхности ![]() равна
сумме площадей боковых граней усечённой
пирамиды.
равна
сумме площадей боковых граней усечённой
пирамиды.
Формулы
![]() (Площадь
боковой поверхности правильной усечённой
пирамиды равна полупроизведению суммы
периметров её оснований и апофемы)
(Площадь
боковой поверхности правильной усечённой
пирамиды равна полупроизведению суммы
периметров её оснований и апофемы)
![]() ,
где
—
площади оснований, а
,
где
—
площади оснований, а ![]() — двугранный
угол при
основании пирамиды.
— двугранный
угол при
основании пирамиды.
Билет 18.1
![]()
Скоростью равномерного движения называют отношение длины пути, пройденного телом, к промежутку времени, за который этот путь пройден:

скорость выразится формулой
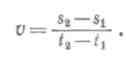
Зная скорость v равномерного движения, можно найти путь, пройденный за любой промежуток времени t, по формуле
s = vt.
Зная путь s, пройденный телом при равномерном движении, и скорость v этого движения, можно найти промежуток времени t, затраченный на прохождение этого пути, по формуле
18.2
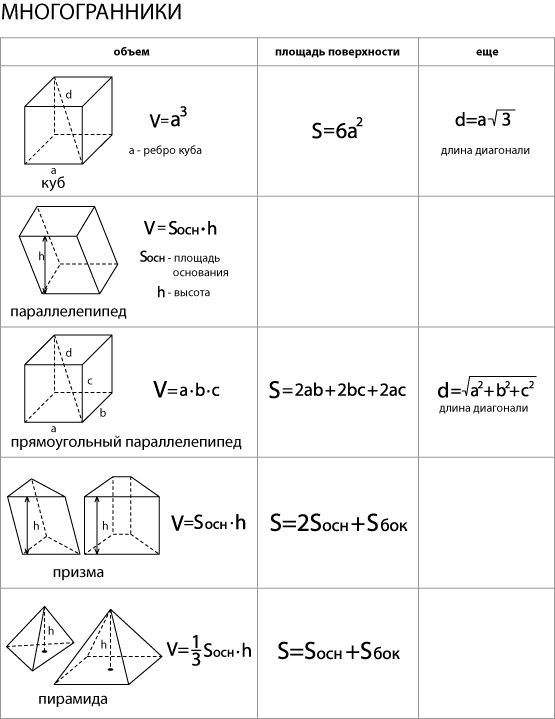
Определение: выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число ребер.
Существует всего 5 видов правильных многогранников:
Тетраэдр
Гексаэдр (Куб)
Октаэдр
Икосаэдр
Додекаэдр
Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине равна 180 градусов. Таким образом, тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Радиус описанной сферы:
![]()
Радиус вписанной сферы:
![]()
Площадь поверхности:
![]()
Объем тетраэдра:
![]()
Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине равна 270 градусов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.
Элементы симметрии:
Куб имеет центр симметрии - центр куба, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
![]()
Радиус вписанной сферы:
![]()
Площадь поверхности куба:
S=a2
Объем куба:
V=a3
Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240 градусов. Таким образом, октаэдр имеет 8 граней, 6 вершин и 12 ребер.
Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
Радиус описанной сферы:
![]()
Радиус вписанной сферы:
![]()
Площадь поверхности:
![]()
Объем октаэдра:
![]()
Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300 градусов. Таким образом икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
![]()
Радиус вписанной сферы:
![]()
Площадь поверхности:
![]()
Объем икосаэдра:
![]()
Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
![]()
Радиус вписанной сферы:
![]()
Площадь поверхности:
![]()
Объем додекаэдра:
![]()
Билет 19.1
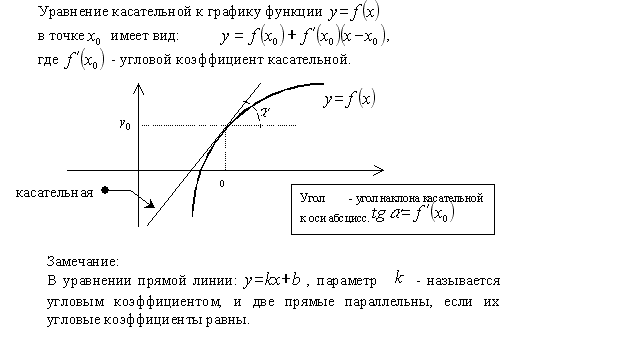
Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Производной
функции f(x)
в точке x0 называется
предел отношения приращения функции в
этой точке ![]() f=f(x0+
x)−f(x0)к
приращению
аргумента
x
при
x
0: f
f=f(x0+
x)−f(x0)к
приращению
аргумента
x
при
x
0: f![]() (x0)=lim
(x0)=lim![]() x
x![]() 0
xf(x0+
x)−f(x0).
0
xf(x0+
x)−f(x0).
Геометрический смысл производной
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
19.2
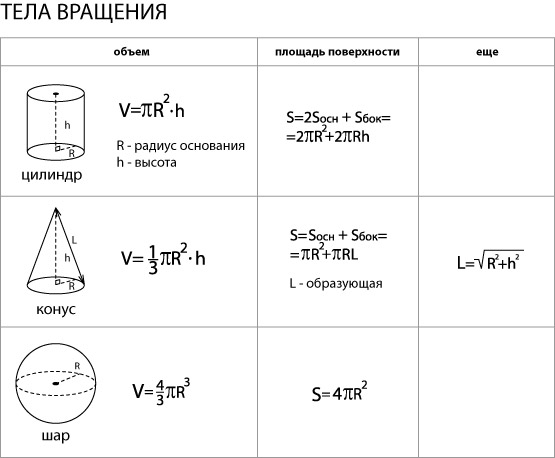
Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей.
Сечение
цилиндра плоскостью, параллельной его
оси, представляет прямоугольник.
Осевым
сечением называется
сечение, которое проходит через ось
цилиндра.
Теорема
Плоскость,
параллельная плоскости основания
цилиндра, пересекает его боковую
поверхность по окружности, равной
окружности основания.
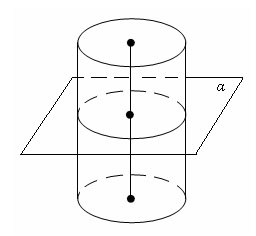 Доказательство
Пусть
α – плоскость, параллельная плоскости
основания цилиндра. Параллельный перенос
в направлении оси цилиндра, совмещает
плоскость α с плоскостью основания
цилиндра, совмещает сечение боковой
поверхности плоскостью α с окружностью
основания. Теорема доказана.
Доказательство
Пусть
α – плоскость, параллельная плоскости
основания цилиндра. Параллельный перенос
в направлении оси цилиндра, совмещает
плоскость α с плоскостью основания
цилиндра, совмещает сечение боковой
поверхности плоскостью α с окружностью
основания. Теорема доказана.
Билет 20.1
Определение
степени с отрицательным показателем:
![]()
Если основание степени с отрицательным показателем дробное, то
![]()
![]() Свойства
степени с отрицательным показателем.
Свойства
степени с отрицательным показателем.
![]() -
произвольные целые числа.
-
произвольные целые числа.
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]() 5.
5. ![]()
20.2
Конусом называется тело. которое состоит из круга - основание конуса, точки, не лежащей в плоскости этого круга - вершины конуса, и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Полная поверхность конуса состоит из основания и боковой поверхности.
Конус называется прямым, если прямая соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.
Осью прямого конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением.
Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.
Конические сечения как результат пересечения плоскости с конусом. Возможны три основных типа конических сечений: эллипс, парабола, гипербола.
Центр тяжести любого конуса лежит на четверти высоты считая от основания.
Боковая
поверхность: S=![]() rl,
где r —
радиус основания, l —
длина образующей.
rl,
где r —
радиус основания, l —
длина образующей.
Полная поверхность: S= r(r+l), где r — радиус основания, l — длина образующей.
Объем кругового конуса: V=31 r2h
Телесный
угол при вершине прямого кругового
конуса: ![]() =2
(1−cos2
=2
(1−cos2![]() ),
где
),
где ![]() —угол
раствора конуса
(т. е. удвоенный угол между осью конуса
и любой прямой на его боковой поверхности).
—угол
раствора конуса
(т. е. удвоенный угол между осью конуса
и любой прямой на его боковой поверхности).
Полная площадь поверхности круглого конуса равна сумме площадей боковой поверхности конуса и его основания. Основание конуса есть круг и его площадь вычисляется по формуле площади круга:
S=π r l+π r2=π r (r+ l)
Билет 21.1
Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу xиз множества X определенное число y, то говорят , что задана функция y = f(x) с областью определения X : y = f(x), D(f) = X.
Значения переменных, на которых задается функция y = f(x) , называют допустимыми значениями переменных.
Область определения функции — множество, на котором задаётся функция
Область значений функции — множество значений, которые принимает функция в результате ее применения
Пусть
задана функция ![]() ,
которая отображает множество
,
которая отображает множество ![]() в
в ![]() ,
то есть:
,
то есть: ![]() ;
тогда
;
тогда
областью значений функции называется подмножество множества вида
![]()
и обозначается
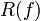 ,
, 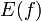 ,
, 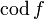 (от
англ. codomain «со-область»)
или
(от
англ. codomain «со-область»)
или 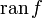 (от
фр. range «со-область»).
(от
фр. range «со-область»).
21.2
Усеченным конусом называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям. Круги O и O1 - его основания, его образующие AA1равны между собой, прямая OO1 - ось, отрезок OO1- высота. Его осевое сечение - равнобедренная трапеция. |
Площадь
боковой поверхности усеченного
конуса: S=
(R1+R2)![]() l
l
Объем усеченного конуса: V=31 H(R12+R1 R2+R22),
где h - высота усеченного конуса; R1,R2 - радиусы верхнего и нижнего оснований; l - образующая.

Билет 22.1
Функция y = f(x) называется четной, если для любого x из области определения функции выполняется равенство f(-x) = f(x).
четные функции: y = /x/, y = x2, y = cos x
График четной функции симметричен относительно оси OY.
Функция y = f(x) называется нечетной, если для любого x из области определения функции выполняется равенство f(-x) = - f(x).
нечетные функции: y = 1/x, y = x3, y = sin x, y = tg x, y = ctg x, y = arcsin x, y = arctg x
График нечетной функции симметричен относительно начала координат O.
Из определения четной и нечетной функции следует, что область определения X как четной, так и нечетной функции должна обладать следующим свойством: если x принадлежит X, то и -x принадлежит X, т.е. X - симметричное относительно начала координат O множество.
22.2
Шаровой, или сферической, поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки — центра шара. Радиус и диаметр шара определяют также как и для окружности.
Шар — это тело ограниченное шаровой поверхностью.
Шар можно получить, вращая полукруг или круг вокруг его диаметра.
|
|
Все плоские сечения шара — круги. С приближением секущей плоскости к центру шара радиус круга увеличивается. Наибольший круг получается в сечении шара плоскостью, проходящей через центр O. Такой круг делит пополам шар. и его поверхность и называется большим кругом. Радиус большого круга равен радиусу шара.
Площадь сферы
![]()
Объем шара, ограниченного сферой
![]()
Площадь сегмента сферы
![]() ,
где H — высота сегмента, а
—
зенитный угол
,
где H — высота сегмента, а
—
зенитный угол
Билет 23.1
Синусом
называется отношение ![]()
Косинусом
называется отношение ![]()
Тангенс
определяется как ![]()
Котангенс
определяется как ![]()
Секанс
определяется как ![]()
Функции ![]() — периодические с
периодом 2π,
функции
— периодические с
периодом 2π,
функции ![]() и
и ![]() —
c периодом π.
—
c периодом π.
23.2
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Если касательная плоскость к сфере определяется как плоскость, имеющая со сферой единственную общую точку, то признак и свойство касательной плоскости формулирутся так:
Признак. Если плоскость проходит через точку сферы перпендикулярно радиусу, проведенному в эту точку, то плоскость касается сферы.
Свойство. Касательная плоскость перпендикулярна радиусу сферы, проведенному в точку касания.
Если же касательная плоскость к сфере определяется как плоскость, проходящая через точку на сфере перпендикулярно радиусу, проведенному в эту точку, то формулировки признака и свойства таковы:
Признак. Если плоскость имеет со сферой единственную общую точку, то она перпендикулярна радиусу, проведенному в эту точку, т.е. является касательной плоскостью.
Свойство. Касательная плоскость имеет со сферой единственную общую точку
Билет 24.1
Градусная мера. Здесь единицей измерения является градус ( обозначение ° ) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. Один градус состоит из 60 минут ( их обозначение ‘ ); одна минута – соответственно из 60 секунд ( обозначаются “ ).
Радианная
мера. Как
мы знаем из планиметрии длина
дуги l,
радиус r и
соответствующий центральный
угол ![]() связаны соотношением:
связаны соотношением:
= l / r .
Эта формула лежит в основе определения радианной меры измерения углов. Так, если l = r , то = 1, и мы говорим, что угол равен 1 радиану, что обозначается: = 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:
Радиан есть центральный угол, у которого длина дуги и радиус равны ( AmB = AO, рис.1 ). Итак, радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.
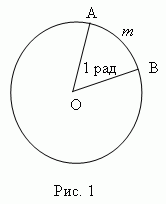
Следуя этой формуле, длину окружности C и её радиус r можно выразить следующим образом:
2 ![]() = C
/ r .
= C
/ r .
Так, полный оборот, равный 360° в градусном измерении, соответствует 2 в радианном измерении. Откуда мы получаем значение одного радиана:
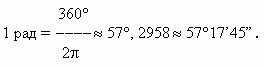
Обратно,
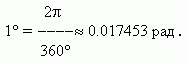
Полезно помнить следующую сравнительную таблицу значений наиболее часто встречающихся углов в градусах и радианах:
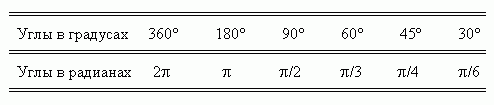
![]() ;
; ![]() ,
,
24.2
надо умножить площадь основания на высоту призмы
Билет 25.1
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Правило исследования функции y=f(x) на экстремум
Найти область определения функции f(x).
Найти первую производную функции f '(x).
Определить критические точки, для этого:
найти действительные корни уравнения f '(x)=0;
найти все значения x при которых производная f '(x) не существует.
Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
Вычислить значение функции в точках экстремума.
ПРИМЕР!
25.2
Vпрямоугольного параллелепипеда V= SH= abc
Билет 26.1
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] . в) Четность, нечетность: функция нечетная.
г)
Периодичность:
функция периодическая с основным
периодом T = 2![]() .
.
д) Нули
функции:
sin x =
0 при x =
n, n ![]() Z.
Z.
е) Промежутки знакопостоянства:
![]() ;
; ![]() .
.
ж) Промежутки
монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
График функции y= sin x изображен на рисунке.
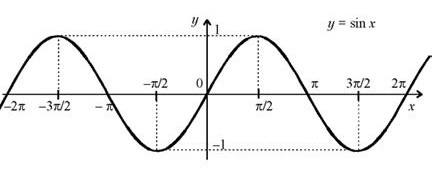
26.2
V цилиндра Pr2 * H
Билет 27.1
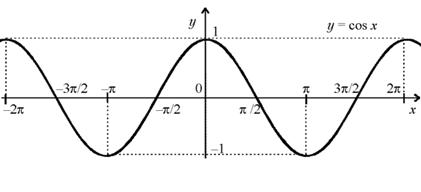
а) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] . в) Четность, нечетность: функция четная.
г) Периодичность: функция периодическая с основным периодом T = 2 .
д) Нули
функции:
cos x =
0 при x = ![]() +
n, n
Z.
+
n, n
Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
. ж) Промежутки монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
График функции y= cos x изображен на рисунке.
27.2
Билет 28.1
а) Область определения: D (tg x) = R \ { /2 + n( n Z ) }.
б) Множество значений: E (tg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = .
д) Нули функции: tg x = 0 при x = n, n Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y = tg x изображен на рисунке.
28.2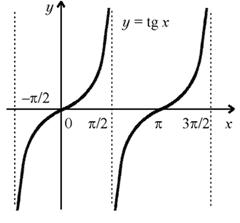
29.1

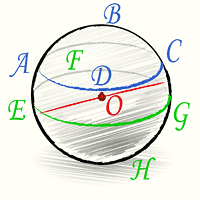 Шар,
Сфера
Шар,
Сфера Меридианы
шара, Меридианы сферы
Меридианы
шара, Меридианы сферы