Ответы по математике. 1. Свойства степени с рациональным показателем

1) Определение. Арифметическим корнем n-й степени (n   N, n  2) из неотрицательного числа a называется такое неотрицательное число, n – я степень которого равна а.

2) Определение. Степень с рациональным показателем

Если

3) Свойства степени с рациональным показателем:

При a > 0, b > 0, p и q - рациональные числа:

а) 

б )

в) 

г) 

д)  .

Степенью числа а > 0 с рациональным показателем   , где m – целое число, а n – натуральное (n > 1), называется число 

Итак, 

Например, 

Степень числа 0 определена только для положительных показателей;

по определению 0^r = 0  , для любого r > 0

Замечания

1. Из определения степени с рациональным показателем следует, что для любого положительного а и любого рационального r число a^r положительно.

2. Любое рациональное число допускает различные записи его в виде дроби, поскольку 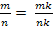 для любого натурального k. Значение а^r также не зависит от формы записи рационального числа r.

3. При а < 0 рациональная степень числа а не определяется.

Для степеней с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (при условии, что основание степени будет положительным).

1.2

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.

Плоскость.  Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
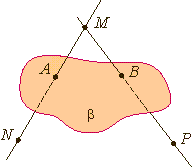
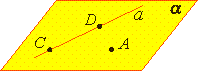
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,

Аксиомы стереометрии и их следствия

Аксиома 1.  Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
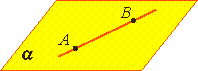
Аксиома 2.  Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
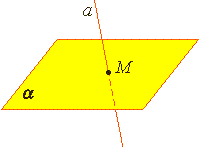
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
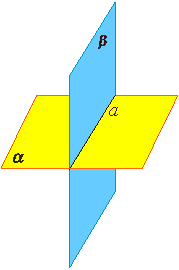
Аксиома 3.  Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты.

Некоторые следствия из аксиом

Теорема 1.  Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
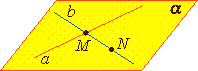
Теорема 2.  Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Билет 2.1

Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а:

√а = b ( при a ≥ 0, b ≥ 0, b² = a).

Пример: √9 = 3 (9 ≥ 0, 3 ≥ 0, 3² = 9)

 При а < 0 выражение √a не имеет смысла.

Пример: √-25 – невозможно извлечь корень: 5² = 25 и -5² = 25 (а не -25)

 

При любом а, при котором выражение √a имеет смысл, верно равенство (√a)² = |а|.

Пример: (√25)² = 5² = 25

√-5² = √25 = 5

 

Свойства арифметического квадратного корня:

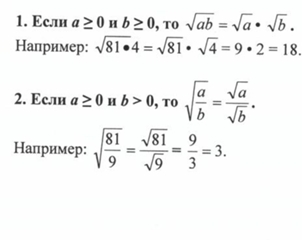 3. (√a)ⁿ  = √aⁿ   (при a ≥ 0)

Например:  (√16)³ = √16³ = √4096 = 64 √16³ = (√16)³ =  4³  =  64

 

Арифметические корни n-й степени.

⁴√81 = 3  (так как 3⁴ = 81)

Читается так: корень четвертой степени из 81 равен 3.

Преобразование выражений с квадратными корнями.

2.2