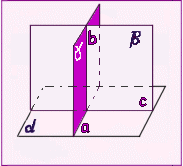
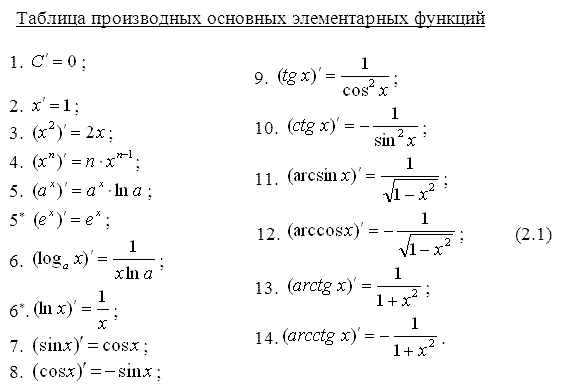
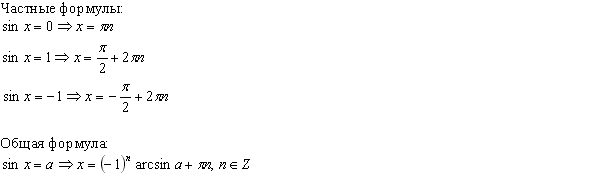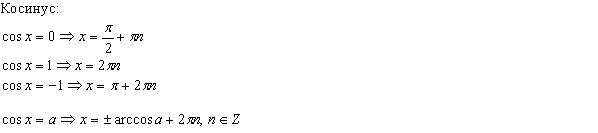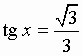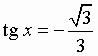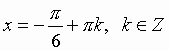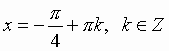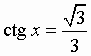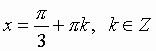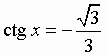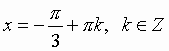Прямая параллельная плоскости.
Прямая параллельна плоскости, когда она параллельна прямой, лежащей в этой плоскости. Если требуется провести прямую параллельно данной плоскости, то сначала надо провести в плоскости какую-либо прямую, а затем провести прямую, ей параллельную, которая будет параллельна данной плоскости. В плоскости можно провести неограниченное число прямых линий, следовательно, можно провести неограниченное количество и прямых, параллельных плоскости.
Определение: прямая параллельна плоскости, если она параллельна прямой, принадлежащей данной плоскости.
Определение 2.3.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Если прямая a параллельна плоскости α, то пишут a || α.
Теорема 2.4. Признак параллельности прямой и плоскости.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
|
Теорема 2.5. Теорема о следе.
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.
|
Определение 2.4.
Прямую b иногда называют следом плоскости β на плоскости α.
Билет 3.1
Арифметическим корнем n-й степени из числа а называют неотрицательное число , n-я
степень которого равна а.
Обозначается арифметический корень n-й степени из числа а
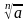 ,
,
где n- показатель корня,
а- подкоренное выражение.
Знак
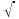 называют
еще радикалом.
называют
еще радикалом.
Арифметический корень второй степени называется корнем квадратным и обозначается √,
арифметический
корень третьей степени называется
кубическим корнем о обозначается
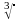
Например :
а)
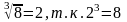 и 2≥0;
и 2≥0;
б)
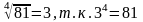 и 3≥0;
и 3≥0;
в)

Из определения арифметического корня n-й степени следует, что при четом n подкоренное выражение должно быть больше или равно нулю, а значит и значение такого корня тоже неотрицательно, например:
арифметический корень 4-й степени из числа -81 не существует, так как ни одно число в четвертой степени не даст -81 ( при возведении в четную степень значение выражения всегда неотрицательно).
При нечетном показателе корня подкоренное выражение может быть отрицательным, и тогда минус может быть вынесен за знак коня.
Например:

Уравнение хn=а.
Уравнение хn=а при нечетном n имеет единственное решение х= .
Например : х3=-125;
х=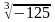 ;
;
х=- ;
;
х=-5.
Для наглядности сделаем проверку:
(-5)3=-125;
-125=-125- верно.
Ответ : х=-5.
Уравнение хn=а при четном n имеет и положительном а имеет два корня
х=± .
.
Например:
х4=16;
х1=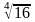 ;
х2=-
;
;
х2=-
;
х1=2; х2=-2.
Можно убедиться при проверке, что 24=16 и (-2)4=16.
Ответ : ±2.
Иногда нужно применить такое свойство арифметического корня n-й степени:
|х|, если n четно;
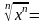 х,
если n нечетно.
х,
если n нечетно.
х, если х≥0;
 Вспомним,
что |х|= -х, если х<0.
Вспомним,
что |х|= -х, если х<0.
Например :
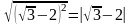 .
.
Так
как
 <0,
следовательно
<0,
следовательно
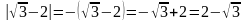 .
.
Для арифметического корня n-й степени, как и для квадратного корня, существуют операции внесения множителя под знак корня и вынесение множителя из-под знака корня.
Например :
2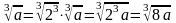 .
.
Из примера видно, что для внесения множителя под знак корня n-й степени его нужно
возвести в n-ю степень. Нужно помнить, что под знак с четным показателем мы имеем право внести только положительный множитель, например:

Аналогично производится вынесение множителя из-под знака корня , например:
а)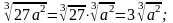
б)
в)

3.2
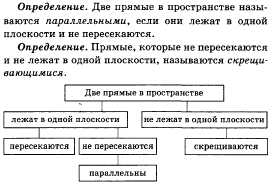
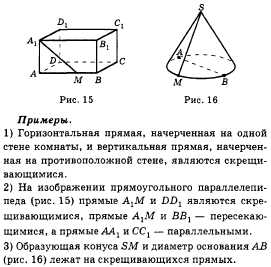
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
|
a || b (прямая а параллельна прямой b) прямая с и прямая а не параллельны прямая с и прямая b не параллельны |
рис. 8 |
|
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
|
M |
рис. 9 |
|
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.
|
отрезок СD || отрезку АВ |
||||
рис. 10 |
|
||||
Свойства параллельных прямых Свойство 1. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Свойство 2. Если две прямые параллельны третьей прямой, то они параллельны.
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
|
|
||||
|
|
Билет 4.1
Логарифм числа b по основанию a (logab) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).
Обозначение: logab.
logab = x, ax = b.
Логарифм числа b по основанию a - logab (a > 0, a ≠ 1, b > 0)
Десятичный логарифм - lg b (Логарифм по основанию 10, а = 10).
Натуральный логарифм - ln b (Логарифм по основанию e, а = e).
Формулы и свойства логарифмов
1° Основное логарифмическое тождество - alogab = b;
2° loga1 = 0;
3° logaa = 1;
4° loga(bc) = logab + logac;
5° loga(b/c) = logab - logac;
6° loga(1/c) = loga1 - logac = - logac;
7° loga(bc) = c logab;
8° log(ac)b = (1/c) logab;
4.2
Теорема Если стороны двух углов соответственно сонаправлены, то такие углы равны. |
|
Рассмотрим углы О и О1 с соответственно сонаправленными сторонами и докажем, что угол O равен углу O1. Отметим на сторонах угла О какие-нибудь точки А и В и отложим на соответственных сторонах угла О1отрезки О1А1=ОА и 01В1=ОВ (рис. 25). Четырехугольник ОО1А1А — параллелограмм, так как противоположные стороны OA и O1A1параллельны и равны. Отсюда следует, что АА1||001 и AA1=OO1. Аналогично четырехугольник OO1BB1 — параллелограмм, поэтому ВВ1||001 и ВВ1=ОО1 Так как АА1||ОО1 и BBl||001, то по теореме о трех параллельных прямых АА1||ВВ1. Кроме того, АА1=001=ВВ1. Таким образом, в четырехугольнике АВВ1А1противоположные стороны АА1 и ВВ1 параллельны и равны. Следовательно, этот четырехугольник — параллелограмм, и значит, стороны АВ и А1В1 равны. Сравним теперь треугольники АОВ и A1O1B1. Они равны по трем сторонам, и поэтому угол O равен углу O1 Теорема доказана.
Билет 5.1
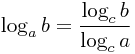
5.2
Определение 2.5.
Две плоскости называются параллельными, если они не имеют общих точек.
Теорема 2.6. Признак параллельности плоскостей.
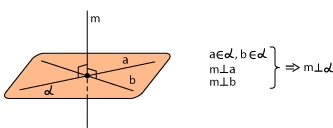
Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны.
Доказательство проведем от противного. Пусть прямые a и b лежат в плоскости β, причем a || α и b || α (чертеж 2.3.1). Если плоскости α и β не параллельны, то они пересекаются по некоторой прямой c. Поскольку a || α, то по теореме о следе c || a. Аналогично получаем, что c || b, тогда a || b. Мы пришли к противоречию, поскольку a и b по условию пересекаются. |
Теорема 2.7.
Если две параллельные плоскости пересечены третьей, то она оставляет на этих плоскостях параллельные следы.
|
|
|
|
Теорема 2.8.
Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
Теорема 2.9.
Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны.
|
|
Чертеж 2.3.3. |
Теорема 2.10.
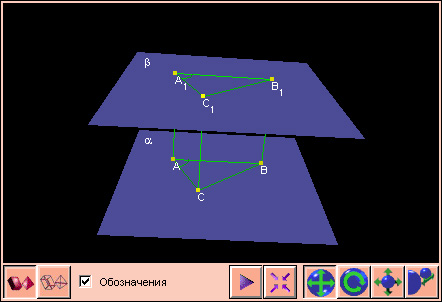
Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях.
На чертеже 2.3.4 показаны углы BAC и B1A1C1, причем AB || A1B1 и AC || A1C1. По признаку параллельности плоскостей плоскость BAC параллельна плоскостиB1A1C1.
Пусть
соответствующие отрезки на сторонах
угла равны: AB = A1B1 и AC = A1C1.
Проведем прямые AA1, BB1, CC1.
Четырехугольник ABB1A1 –
параллелограмм, так как AB = A1B1 и AB || A1B1,
следовательно, AA1 = BB1 и AA1 || BB1.
Аналогично докажем, что AA1 = CC1.
Отсюда следует, что BB1 = CC1 и BB1 || CC1,
следовательно, CBB1C1 –
параллелограмм и CB = C1B1.
Теперь утверждаем, что Δ ABC = Δ A1B1C1,
откуда
Билет 6.1
Логарифмы
по основанию 10 (обозначение:
Кроме
того, при переносе десятичной запятой
в числе на Связь с натуральным логарифмом:
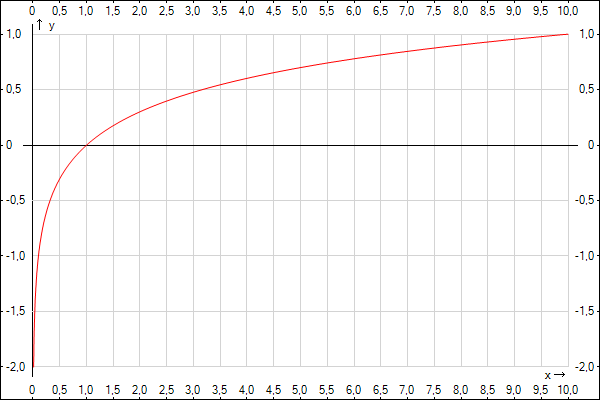
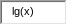
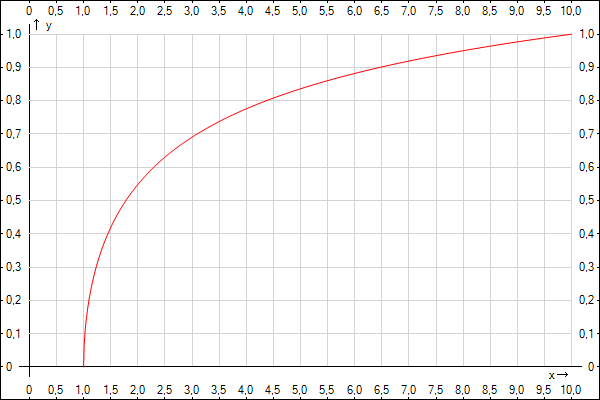
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал. y = lg(x) - десятичный логарифм от х
Текст
формулы:
y(x) =
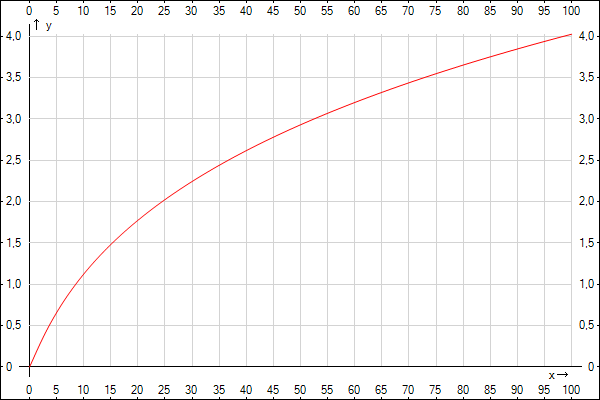
y = lg(1/2)(x) - корень квадратный от десятичного логарифма от x
Текст
формулы:
y(x) =
y = lg(x+1)lg(x+2) - произведение десятичных логарифмов
Текст
формулы:
y(x) =
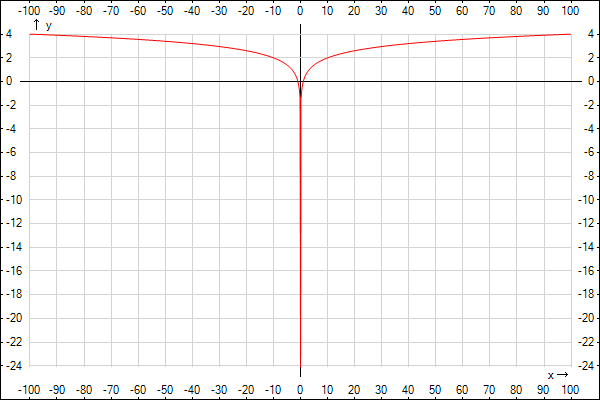
y = lg(x^2) - десятичный логарифм от квадрата x
Текст
формулы:
y(x) =
6.2 Определение Прямая, пересекающая плоскость, перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку называется перпендикулярной этой плоскости, если она пересечения. Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости. Теорема 2 1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой Теорема 3 2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Билет 7.1 Теорема.
Пусть Рассмотрим
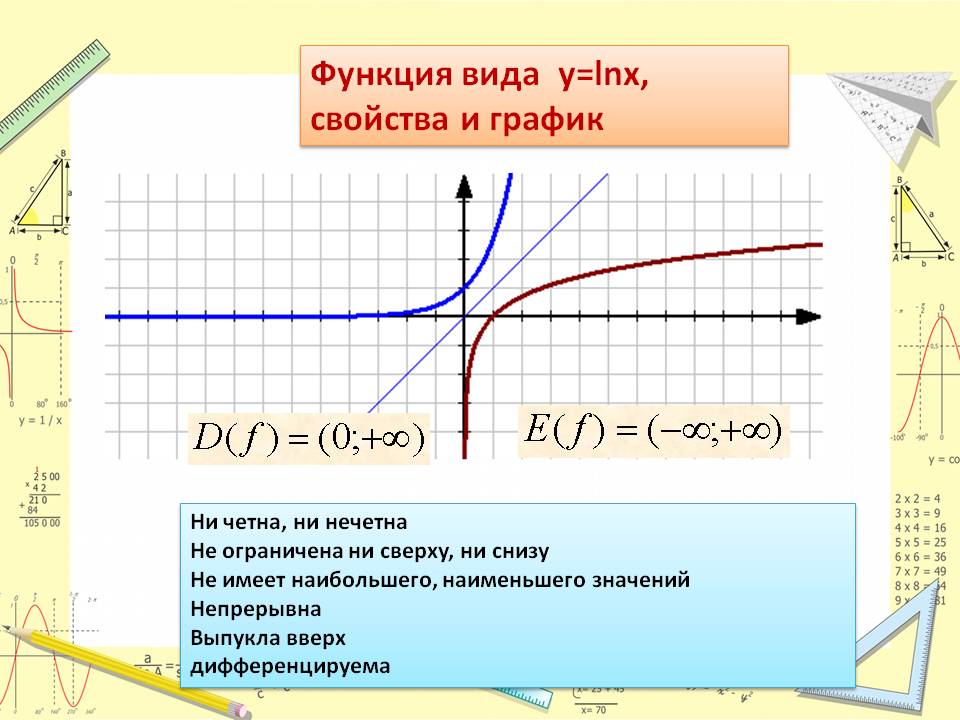
функцию Обозначение: Свойства натурального логарифма 1. Область определения натурального логарифма . 2. 3. Натуральный
логарифм – дифференцируемая функция,
и 4. Натуральный логарифм строго возрастает, так как . 5.
7.2 Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость. Пусть требуется найти расстояние от точки K до плоскости s (АВС).
Расстояние между параллельными плоскостями определяется длиной перпендикуляра, опущенного из произвольной точки одной плоскости до другой. Аналогично находится расстояние от плоскости до параллельной ей прямой. На прямой берется точка и находится расстояние до плоскости.
Билет 8.1
При a >
0, a
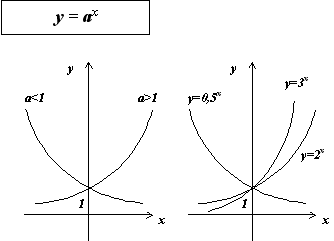
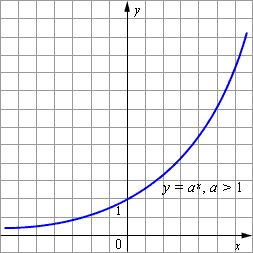
Основные свойства показательной функции y = a x при a > 1:
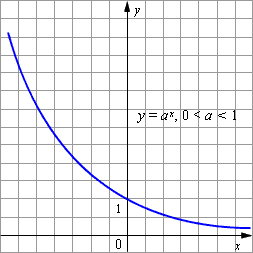
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.
Основные свойства показательной функции y = a x при 0 < a < 1:
К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:
8.2
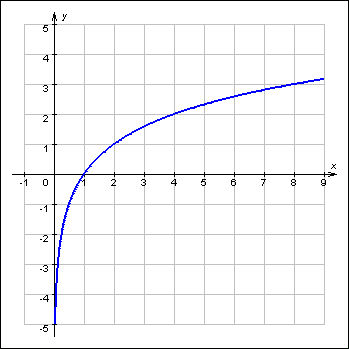
Билет 9.1 На промежутке (0; +∞) определена функция, обратная к ax (a > 0, a ≠ 1). Эта функция называется логарифмической:
Логарифмическая функция непрерывна и строго возрастает (если основание a > 1) или строго убывает (если 0 < a < 1) на всей области определения. Множество ее значений – все действительные числа. Так как логарифмическая и показательная функции взаимно обратны, то при a > 0, a ≠ 1,
Ниже
приведены некоторые свойства
логарифмов
(x > 0,
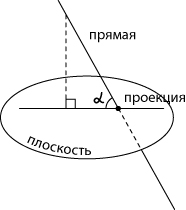
9.2 Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной. Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получилипроекцию наклонной на плоскость.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол. Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю. Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°. Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Это определение. Но как же с ним работать? Как проверить, что данная прямая перпендикулярна всем прямым, лежащим в плоскости? Ведь их там бесконечно много. На практике применяется признак перпендикулярности прямой и плоскости: Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Билет 10.1 Функция, заданная формулой y = ax2 + bx + c , где x и y - переменные, а a, b, c - заданные числа, причем a =0 , называется квадратичной функцией. График квадратичной функции - парабола. Если a > 0 , то ветви параболы направлены вверх. Если a < 0 , то ветви параболы направлены вниз. График квадратичной функции называется параболой.
Любая
квадратичная функция представима в
виде
Координаты
вершины параболы:
Прямая
При
10.2 Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книге. У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре. Величины двугранных углов правильных многогранников:
где φ = (1 + √5)/2 — золотое сечение. Билет 11.1 Справедлива следующая теорема.
Свойства
функции
1)
11.2
Билет12.1
12.2 Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными. Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники. Длины трёх ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Куб — прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты. Параллелепипед симметричен относительно середины его диагонали. Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам. Противолежащие грани параллелепипеда параллельны и равны. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений
В параллелепипеде: 1) противолежащие грани равны и параллельны; 2) все четыре диагонали пересекаются в одной точке и делятся в ней пополам. Доказательства:
1)
Для любой пары противолежащих граней
параллелепипеда имеем: соответствующие
углы равны (например,
Теорема 3 В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений (т. е. трех ребер, выходящих из одной вершины). Следствие В прямоугольном параллелепипеде все диагонали равны. Билет 13.1 Простейшими называются тригонометрические уравнения следующих четырёх видов: sin x = a; cos x = a; tg x = a; ctg x = a:
Общий вид решения уравнения tg x = a определяется формулой: x = arctg(a) + pk, k Î Z (целые числа). Общий вид решения уравнения ctg x = a определяется формулой: x = arcctg(a) + pk, k Î Z (целые числа).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Уравнение: |
Уравнение: |
РЕШЕНИЯ: |
|
*** |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*** |
|
|
13.2
Призма — многогранник, две грани которого являются конгруэнтными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Призмы бывают прямые и наклонны
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
Основания призмы являются равными многоугольниками.
Боковые грани призмы являются параллелограммами.
Боковые ребра призмы параллельны и равны.
Объём призмы равен произведению её высоты на площадь основания:
![]()
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Площадь боковой поверхности произвольной призмы
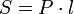 ,
где
,
где 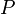 —
периметр перпендикулярного сечения,
—
периметр перпендикулярного сечения, 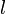 —
длина бокового ребра.
—
длина бокового ребра.Площадь боковой поверхности правильной призмы
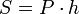 ,
где
—
периметр основания призмы, ,
,
где
—
периметр основания призмы, , 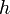 —
высота призмы.
—
высота призмы.Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
Перпендикулярное сечение перпендикулярно ко всем боковым граням.

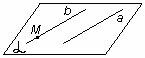
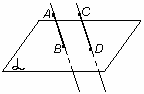
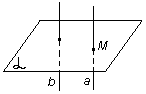 рис.
11
рис.
11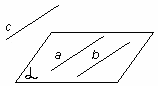 рис.
12
рис.
12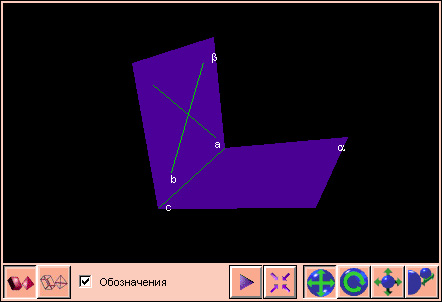
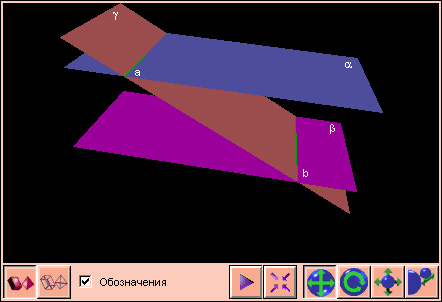 Пусть α и β параллельны, γ –
третья плоскость, которая пересекает
их, причем α
Пусть α и β параллельны, γ –
третья плоскость, которая пересекает
их, причем α 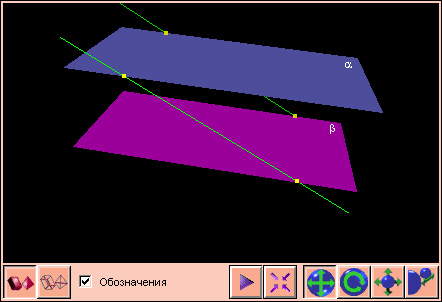




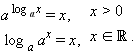
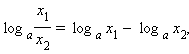
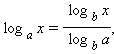

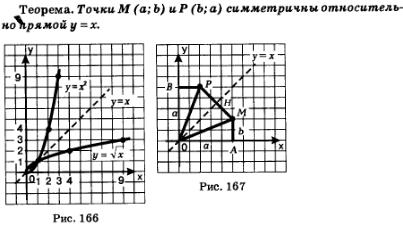 Доказательство. Будем
считать для определенности, что а и b
— положительные числа. Рассмотрим
треугольники ОАМ и ОВР (рис. 167). Они
равны, значит, ОР = ОМ и
Доказательство. Будем
считать для определенности, что а и b
— положительные числа. Рассмотрим
треугольники ОАМ и ОВР (рис. 167). Они
равны, значит, ОР = ОМ и
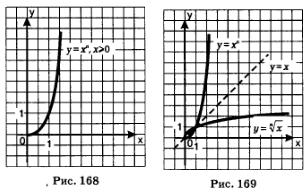 Сформулируем
общий вывод: график функции
Сформулируем
общий вывод: график функции