4.Анализаторы гармоник. Регистраторы формы сигнала.

Анализируемый сигнал, являющейся известной функцией напряжения от времени u(t), графически представляют в декартовой системе координат. Ось абсцисс – время, ось ординат – напряжение. Такой график называется формой электрического сигнала.

При экспериментальном исследование электрических сигналов их форма определяется путем снятия осциллограмм напряжения сигнала. Для безыскаженного воспроизведения формы сигнала необходимо обеспечить строго линейную зависимость между временем и значением координаты осциллограммы по оси абсцисс.

Запись осциллограмм в электромеханических осциллографах осуществляется световым лучом, а в электронных осциллографах – электронным лучом.

В зависимости от количественных значений отдельных характеристик осциллографы делят на 4 класса. Основными характеристиками, определяющими класс осциллографа, является основная погрешность измерения напряжения, основная погрешность коэффициента отклонения, основная погрешность измерения временных интервалов. Так основная погрешность измерения напряжения и основная погрешность измерения временных интервалов для осциллографов класса точности 1,2,3,4 составляют 3,5,10 и 12% соответственно.

5. Измерение параметров модуляции. Основные виды модуляции и измеряемые параметры

Амплитудная модуляция

Математическую модель сигнала модулированного по амплитуде можно представить:

U_AM(t)=U_m(1+McosΩt)cos wt , где U_m – амплитуда немодулированного частотного сигнала, w=2πf, f – несущая частота, Ω=2πF, F – модулирующая частота, M – коэффициент амплитудной модуляции, который численно равен отношению приращения амплитуды ∆U к амплитудному значению напряжения U_m:

M=∆U/ U_m *100%

С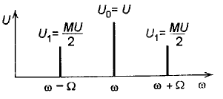 пектр, соответствующий U_AM(t):

Процедура измерения в данном случае сводится к измерению с помощью анализатора спектра амплитуды спектральной линии на несущей частоте (U₀) и амплитуды спектральной линии на любой из боковых частот (U₁). Коэффициент амплитудной модуляции определяется соотношением: M=2U₁/ U₀

Частотная модуляция

Гармонический сигнал, модулируемый по частоте записывается след. образом:

U_ЧM(t)=U₀ cos[(w₀+βsinΩt)t], где U₀ – амплитуда напряжения несущей частоты f₀, w₀=2πf₀, Ω=2πF, F – частота модулирующего напряжения, β=∆w/w=∆f/F – индекс частотной модуляции, ∆f – отклонение сигнала от f₀ при модуляции частоты (девиация)

Девиация частоты пропорциональна амплитуде моделирующего напряжения (U_F): ∆f=aU_F

Рассмотрим спектральный метод измерения параметров ЧМ сигналов (метод нулей функции Бесселя)

При гармоническом законе модуляции ряд Фурье ЧМ сигнала:

U_ЧМ(t)=U_m J_k(β)sin(w+kΩ)t, где J_k(β) – функции Бесселя первого рода к-го порядка.

Спектр ЧМ сигнала:

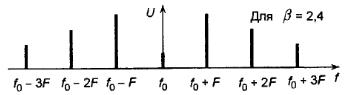
При к=0 напряжение несущей частоты: U=U_mJ₀(β)sinw₀t. При равенстве индекса модуляции β корням бесселевой функции амплитуда сигнала несущей частоты обращается в ноль, т.е. исчезает из спектра.

На основе данного явления (U₀J₀(β)=0) разработан метод измерения девиации частоты, получивший название метода исчезающей несущей. Суть метода заключается в регистрации по шкале анализатора спектра момента обращения в нуль спектральной составляющей. Увеличивая амплитуду модулирующего сигнала можно определить момент исчезновения несущей – этому моменту соответствует первый корень Бесселевой функции, равный 2.4, следовательно, β₁=∆f/F=2.4, ∆f₁=β₁F=2.4F

Метод является высокоточным, но трудоемким.