
- •Введение Постановка задачи
- •1.Общая теория кривых второго порядка
- •1.1 Кривые второго порядка
- •1.2 Классификация кривых второго порядка
- •2.Исследование кривой второго порядка
- •2.1 Определение зависимости типа кривой от параметра с помощью инвариантов
- •Кривая поверхность порядок
- •2.2 Построение кривых при различных значениях параметра
- •3.2 Исследование формы поверхности второго порядка методом сечения плоскостями
- •4. Исследование поверхности второго порядка
- •4.1 Приведение уравнения поверхности к каноническому виду
- •4.2 Исследование формы поверхности методом сечений плоскостями
- •4.3 Построение поверхности в канонической системе координат
- •Список используемой литературы
3.2 Исследование формы поверхности второго порядка методом сечения плоскостями
Если дано каноническое уравнение поверхности S, то представление о поверхности можно получить по форме линий пересечения ее плоскостями:
Z = h — параллельными координатной плоскости XO'Y,
X = h — параллельными координатной плоскости YO'Z,
Y = h — параллельными координатной плоскости XO'Z.
Уравнения
проекций линий пересечения поверхности
S
c
этими плоскостями на соответствующие
координатные плоскости
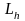 получаются в результате подстановки в
каноническое уравнение поверхности S
Z
=
h,
X
=
h,
Y
=
h
соответственно.
получаются в результате подстановки в
каноническое уравнение поверхности S
Z
=
h,
X
=
h,
Y
=
h
соответственно.
4. Исследование поверхности второго порядка
Дано уравнение поверхности второго порядка:
S:

4.1 Приведение уравнения поверхности к каноническому виду
Положим:
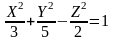 .(4.1)
.(4.1)
Уравнение (4.1) каноническое.
4.2 Исследование формы поверхности методом сечений плоскостями
Каноническое уравнение поверхности (4.1) задает однополостный гиперболоид.
1.
Рассмотрим линии
 полученные в сечениях гиперболического
параболоида плоскостями Z
= h
(h
= const).
Эти линии определяются системой
уравнений:
полученные в сечениях гиперболического
параболоида плоскостями Z
= h
(h
= const).
Эти линии определяются системой
уравнений:

 (4.2)
(4.2)
Следовательно,
 — уравнение проекций линий
— уравнение проекций линий
 на плоскость XO'Y.
на плоскость XO'Y.
Запишем полученное уравнение в виде:
 (4.3)
(4.3)
Уравнение
(4.3) определяет семейство эллипсов с
центром в точках
 и вершинами в точках
и вершинами в точках
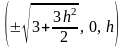 и
и
 .
Действительные оси эллипсов параллельны
осям O'X
и O'Y.
.
Действительные оси эллипсов параллельны
осям O'X
и O'Y.
Полуоси
эллипсов :
 и
и
 увеличиваются с увеличением h.
увеличиваются с увеличением h.
При различных значениях h получим семейство соответствующих эллипсов:

Если h < 0, то уравнение (4.3) не меняет вида .
Используя полученные данные, построим «карту» (см. рис.8).

Рис. 8. Сечения плоскостями, параллельными XO'Y
Рассмотрим
линии
 полученные в сечениях гиперболического
параболоида плоскостями Y
= h.
Эти линии определяются системой
уравнений:
полученные в сечениях гиперболического
параболоида плоскостями Y
= h.
Эти линии определяются системой
уравнений:

Следовательно,
уравнение проекций линий
 на плоскость YO'Z
имеет вид:
на плоскость YO'Z
имеет вид:
 (4.4)
(4.4)
Запишем уравнение (4.4) в виде:
 (4.5)
(4.5)
Уравнение
(4.5) определяет семейство
гипербол в
плоскостях Y
= h
(h
— любое
действительное число) с фокусами в
точках
 и
и
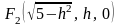 ,
полуосями
,
полуосями
 и
и
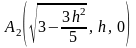 .
.
При
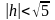 получим
семейство соответствующих гипербол:
получим
семейство соответствующих гипербол:

При
 уравнение
(4.4) определяет две пересекающиеся
прямые.
уравнение
(4.4) определяет две пересекающиеся
прямые.
При
 запишем:
запишем:
 (4.6)
(4.6)
Уравнение
(4.6) определяет семейство гипербол,
которые повёрнуты на
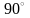 относительно
осей координат.
относительно
осей координат.

Используя полученные данные, построим «карту» (см. рис.9).
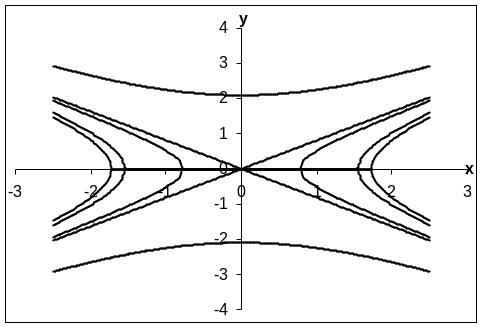
Рис. 9. Сечения плоскостями, параллельными XO'Z
Рассмотрим
линии
 ,
полученные в сечениях однополостного
гиперболоида плоскостями Z
= h.
Эти линии определяются системой
уравнений:
,
полученные в сечениях однополостного
гиперболоида плоскостями Z
= h.
Эти линии определяются системой
уравнений:

Следовательно, уравнения проекций линий на плоскость YO'Z имеют вид
 (4.7)
(4.7)
Запишем уравнение (4.5) в виде:
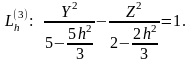 (4.8)
(4.8)
Уравнения
(4.8) — это уравнения гипербол
в плоскостях
 (h
— любое действительное число), с фокусами
в точках
(h
— любое действительное число), с фокусами
в точках
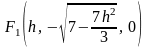 и
и
 ,
полуосями
,
полуосями
 и
и
 .
.
При
 получим семейство соответствующих
гипербол:
получим семейство соответствующих
гипербол:

При
 уравнение (4.7) определяет две пересекающиеся
прямые.
уравнение (4.7) определяет две пересекающиеся
прямые.
При
 запишем уравнение (4.7) в виде:
запишем уравнение (4.7) в виде:

Уравнение (4.6) определяет семейство гипербол, которые повёрнуты на относительно осей координат.

Используя полученные данные, построим «карту» (см. рис.10).
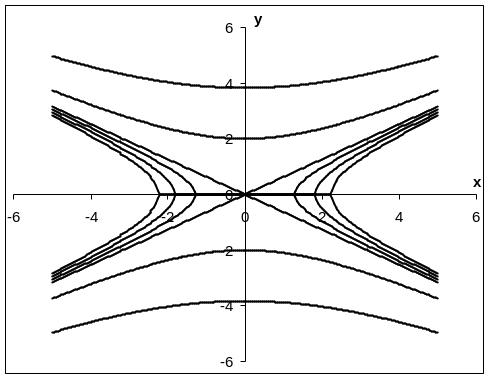
Рис. 10. Сечения плоскостями, параллельными YO'Z
Проанализировав уравнение и результаты исследования методом сечений плоскостями, отметим следующее:
уравнение задаёт однополостный гиперболоид.
оси O'X , O'Y, O'Z являются осями симметрии поверхности, плоскости O'XZ , O'YZ , O'XZ — плоскостями симметрии. Центром симметрии у поверхности является точка O(0,0,0);
рассекая поверхность горизонтальными плоскостями Z = h, в сечениях получаем эллипсы .
4. рассекая поверхность вертикальными плоскостями X = h и Y = h (h – любое действительное число), в сечениях получаем гиперболы.
Поверхность однополостного гиперболоида бесконечна в направлении всех трех координатных осей. Построим её в канонической системе координат (см. рис. 11).
