3°. Достаточные условия экстремума.
Пусть Р(а; b) — стационарная точка функции f(х,у), т.е. df(а, b) = 0. Тогда:
а) если d2f (а, b) < 0 при dx^2 + dy^2 > 0 , то f(а, b) есть максимум функции f (х, у);
б) если d2f (а, b) > 0 при dx^2 + dy^2 > 0 , то f(а, b)есть минимум функции f (х,у);
в) если d2f (а, b) меняет знак, то f (а, b) не является экстремумом функции f (х, у).
Приведенные условия эквивалентны следующим: пусть fx' (a,b) = fy' (a,b) = 0и
A=fxx ''(a,b),B= fxy''(a,b),C=fyy''(a,b) Составим дискриминант Δ=AC — B².
Тогда: 1) если Δ > 0, то функция имеет экстремум в точке Р (а; b) а именно максимум, если A<0
(или С<0), и минимум, если A>0 (или С>0);
2) если Δ < 0, то экстремума в точке Р(а; b) нет;
3) если Δ=0, то вопрос о наличии экстремума функции в точке Р(а; b) остается открытым
(требуется дальнейшее исследование).
Билет 13
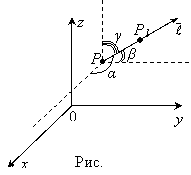
Скалярное поле.Производная по направлению. |
Пусть
в пространстве Oxyz имеется
область D,
в которой задана функция
Рассмотрим
точки области D,
в которых функция поля имеет постоянное
значение C:
Наряду
со скалярными полями в пространстве
рассматривают также п Пусть задана дифференцируемая функция скалярного поля .
Рассмотрим
точку
Производной
функции
в
точке P по
направлению
(обозначают
Заметим:
если
По
условию функция
дифференцируема,
значит, ее полное приращение можно
представить в виде
Перейдем
к пределу при
Если
направление
совпадает
с направлением какой–либо из осей
координат, то
совпадает
с соответствующей частной производной.
Пусть, например, луч
направлен
по оси Oy.
Тогда Для
плоского скалярного поля |
.
В этом случае говорят, что в
области D задано скалярное
поле, а
функцию
называют функцией
поля (например,
скалярное поле температур, скалярное
поле давлений).
.
Совокупность этих точек образует
некоторую поверхность, которая
называется поверхностью
уровня, илиэквипотенциальной
поверхностью. Уравнение
–
уравнение поверхности уровня. При
различных значениях C получим семейство
поверхностей уровня.
лоские
скалярные поля. Функция плоского
скалярного поля имеет вид 
.
Плоские скалярные поля изображаются
геометрически с помощьюлиний
уровня 
(например,
изотермы на картах синоптиков).
этого
поля и луч 
,
выходящий из точки P в направлении
единичного вектора 
где 
–углы,
образованные вектором 
с
осями координат (рис.18). Пусть 
– какая-нибудь
другая точка этого луча. Обозначим 
–
расстояние между
точками P и 
; 
называютвеличиной
перемещения. Приращением функции
в направлении
назовем
разность 
.
)
называется предел отношения приращения
функции в направлении
к
величине перемещения
при
: 
.
в
точке P,
то функция в этом направлении возрастает,
если 
– убывает.
Можно сказать, что производная
по направлению дает скорость изменения
функции в этом направлении.
,
где
.
Разделим обе части на
: 
.
,
учитывая, что 
, 
, 
, 
, 
.
Получим формулу вычисления производной
по направлению: 
.
,
то есть 
, 
и 
.
.