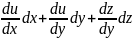Частные производные

Пусть задана функция z = f(х; у). Так как х и у — независимые переменные, то одна из них

может изменяться, а другая сохранять свое значение. Дадим независимой переменной х

приращение Δx ; сохраняя значение у неизменным. Тогда z получит приращение, которое

называется частным приращением z по х и обозначается z_xΔ . Итак,z_xΔ=f(x+Δx;y)−f(x;y).

Аналогично получаем частное приращение z по у:z_yΔ=f(x;y+Δy)−f(x;y).

Полное приращение Δz функции z определяется равенством Δz=f(x+Δx;y+Δy)−f(x;y).

Если существует предел 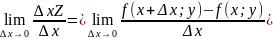то он называется частной производной функции z =f(х; у) в точке М(х; у) по переменной х и обозначается одним из символов:z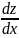’_{x ,} f’_x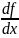

Частные производные по x; в точке М_о(x₀;y₀) обычно обозначают символами Аналогично определяется и обозначается частная производная от z = f(x;у) по переменной у:z’_y= Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(х; у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

Билет 12

Полный дифференциал функции

1°. Полное приращение функции.Пусть функция z = f(x;у) определена в некоторой окрестности точки М(х;у). Полным приращением функции z=f(х,у) называется разность

Δz = Δf (x, y) = f (x + Δx, y + Δy) − f (x, y) .

2°. Полный дифференциал и дифференцируемость функции. Составим полное приращение функции в точке М:Δz = f (x + Δx; y + Δy) − f (x; y) . Функция z = f(x; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде

Δz = A⋅ Δx + B ⋅ Δy +α ⋅ Δx + β ⋅ Δy , (1) гдеα =α (Δx;Δy)→0 и β = β (Δx;Δy)→0 при Δx→0,Δy →0 .

Сумма первых двух слагаемых в равенстве (1) представляет собой главную часть

приращения функции. Главная часть приращение функции z = f(х; у), линейная относительно Δx и Δy , называется полным дифференциалом этой функции и обозначается символом dz:

dz = A⋅ Δx + B ⋅ Δy . (2) Выражения A⋅ Δx и B ⋅ Δy в равенстве (1) называют частными дифференциалами. Для независимых переменных х и у полагают Δx = dx и Δy = dy . Поэтому равенство (2) можно переписать в виде dz = A⋅ dx + B ⋅ dy . (3)

Теорема 1 (необходимое условие дифференцируемости функции). Если функция z = f(x;

у) дифференцируема в точке М(х;у), то она непрерывна в этой точке, имеет в ней частные

производные и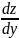 , причем =А, = В.

Теорема 2 (достаточное условие дифференцируемости функции). Если функция z=(x;у) имеет непрерывные частные производные x z′ и y z′ в точке М(х;у), то она дифференцируема в

этой точке.

Функция заведомо имеет полный дифференциал в случае непрерывности ее частных

производных. Если функция имеет полный дифференциал, то она называется дифференцируемой. Дифференциалы независимых переменных совпадают с их приращениями, т. е. dx=Δx и dy=Δy. Полный дифференциал функции z=f(x,y) вычисляется по формуле

dz= Аналогично, полный дифференциал функции трех аргументов u=f(х, у, z) вычисляется по формуле du=