Билет 1

Дифференциалом функции у =f(х) в точке х называется главная часть её приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df (x)): dy=f ′ (x)⋅Δx.Дифференциал dy называют также дифференциалом первого порядка. Найдём дифференциал независимой переменной х, т.е. дифференциал функции у = х. Так как у' = х' = 1, то, согласно формуле, имеем dy = dx=Δx, т.е. дифференциал независимой переменной равен приращению этой переменной: dx = Δx.Поэтому формулу можно записать так:dy = f ′(x) dx,иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной. Из формулы следует равенство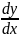 = f ^′(x) Теперь обозначение производной можно рассматривать как отношение дифференциалов dy и dx.

Геометрический смысл дифференциала функции

Д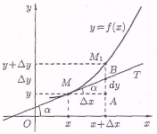 ля этого проведём к графику функции у = f (х) в точке М (х; у) касательную МТ и рассмотрим ординату этой касательной для точки х + Δх На рисунке ⏐АМ⏐=Δх, ⏐АМ₁⏐=Δу. Из прямоугольного треугольника МАВ имеем: tgα=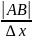 , т.е. ⏐АВ⏐= tg α ⋅Δх.Но, согласно геометрическому смыслу производной, tg α = f ′ (х). Поэтому АВ = f ′ (х)⋅Δх.Сравнивая полученный результат с формулой получаем dy = АВ, т.е. дифференциал функции у = f (х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение Δх.

Билет 2

Определение производной, её геометрический и механический смысл

Рассмотрим две задачи, приводящие к понятию производной функции.

Задача 1. Пусть материальная точка движется по прямой в одном направлении. Обозначим S

– путь, пройденный точкой, а t – время. Путь, пройденный точкой за время t зависит от t и

изменяется по некоторому закону S = S (t). Отметим некоторый момент времени t₀ и поставим

задачу определить скорость материальной точки V₀ в момент времени t0. Для этого рассмотрим

другой момент времени по прошествии отрезка Δt, т.е. момент t₀ + Δt. К моменту t₀ путь,

пройденный точкой, составит S (t₀), в момент t₀ + Δt будем иметь путь S (t₀+ Δt). За

промежуток времени Δt точка прошла путь ΔS = S (t₀ + Δt )− S (t₀ ) Средняя скорость движения

за время Δt составит отношение V_cp=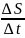 Эта средняя скорость отличается от мгновенной

скорости в момент t₀, и тем ближе величина V_ср к скорости V0, чем меньше промежуток Δt.

Устремим Δt к нулю (пишут Δt →0 ), тогда предел, к которому стремится средняя скорость, и

является скоростью нашей точки V0 момент t₀.V₀=

В последней формуле рассматривается предел отношения приращения пути ΔS к

приращению времени Δt.

Задача 2. Рассмотрим график непрерывной функции y = f (x). Возьмём на этом графике

точку M₀(x₀,y₀) и поставим задачу написать уравнение касательной прямой к графику

y = f (x), проведённой в точке M₀

Т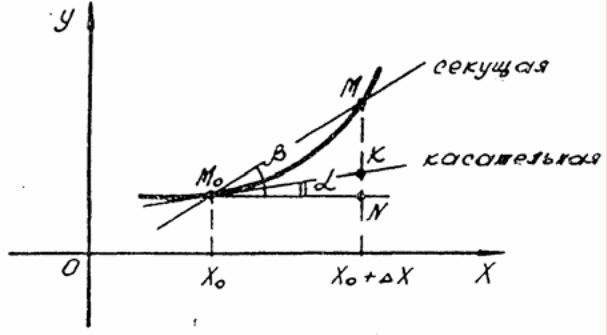 очка M₀ имеет координаты (x₀,y₀) =f(x₀) ; дадим переменной x приращение Δx ипереместимся по графику из точки M₀ в точку M (в нашем случае Δx>0 и мы переместились вправо от точки M₀). Координаты M можно вычислить. Абсцисса M равна x₀+Δx, а ордината y = f (x₀ + Δx). На сколько изменилось значение функции y = f (x) при перемещении из точки M₀ в точку M? Это изменение функции называется приращением функции, обозначается Δy и вычисляется так:

Δy =f (x₀ + Δx )−S (x₀ ) В случае нашей функции (возрастающая) Δy>0. Прямая M₀M называется секущей и её наклон к оси Oх определяется тангенсом угла β. Угловой коэффициент секущей

K_сек=tgβ=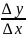 Если теперь неограниченно уменьшать приращение Δx, Δx →0 , то приращение функции

Δy→0 (наша функция непрерывна). При этом секущая M0M неограниченно приближается к

положению M₀K. Это предельное положение секущей и есть прямая, которая является

касательной к графику y = f (x) в точке M₀. Угол β наклона секущей к положительному

направлению оси OX превратится в угол наклона касательной α. Тогда угловой коэффициент

касательной прямой K получим так: K=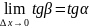 = 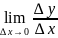т.е. угловой коэффициент

касательной есть предел отношения приращения функции Δy к приращению аргумента Δx при

стремлении Δx к нулю.

Производной функции y = f (x) в точке x0 называется предел отношения приращения

функции Δy = f (x0 + Δx) – f (x0) к приращению аргумента Δx при произвольном стремлении Δx к

нулю, если такой предел существует. Обозначается производная функции f (x) в точке x0

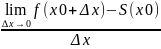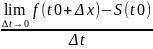символом f ′(x₀). Итак, f ′(x₀)= Из рассмотренных ранее задач получаем, что скорость прямолинейного движения материальной точки в момент времени t0 есть производная от пути по времени S ′(t₀)= =V(t₀) В этом состоит механический смысл производной. Вторая задача приводит нас к геометрическому смыслу производной. Мы получили, что угловой коэффициент касательной к кривой проведённой в точке M₀(x₀,y₀), есть y = f’(x₀)