I. Длина дуги кривой в декартовых координатах.
Дана функция y= ƒ(x), непрерывная на отрезке [a,b], вместе с ƒ '(x).
Определение:за длину дуги кривой принимается предел, к которому стремится длина вписанной ломанной линии, когда число звеньев этой ломанной неограниченно увеличивается.
B
ΔLi
y
ƒ(x) Δyi
Δxi
ΔL1
A
ξi
0 a=x0 x1 xi-1 xi b=xn x
Разобьем отрезок [a,b]наnчастей точкамиa0 =x0<x1<..<xi-1<xi<..<xn =b;
Проведем ординаты через точки деления и соединим хордами их концы. Длины звеньев ломанных обозначим: ΔL1, ΔL2, …, ΔLi, …, ΔLn.
Проведем прямую параллельную Ох .
Δyi = ƒ(xi) - ƒ(xi-1).
Длина ломанной линии Ln :
Ln
=
,
а длина кривой по определению:L=
ΔLn
=
;
Найдем ΔLi.
ΔLi
=
=
;
;
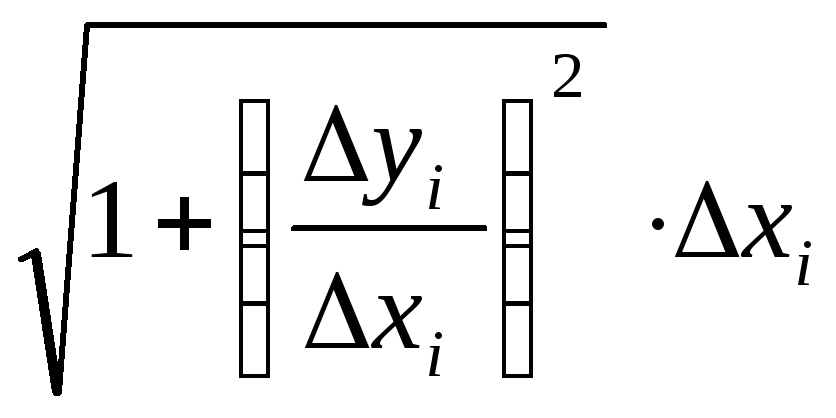( по теореме Лагранжа)
так
поступаем с каждым звеном, тогда ΔLi
=
,
так как по условию ƒ(x)
и ƒ´(x) непрерывны на
отрезке [a,b],
то функция
- непрерывна на отрезке [a,b],
а значит существует определенный
интеграл:
dx.
Итак,
L=
=
dx=
dx.
Пример: найти длину окружности.
x2 + y2 = a2;
y=
;
значитL= 4
dx;
y´
=
;
4
dx = 4
dx = 4a
= 4a arcsin
=
4a (π/2) = 2πa.
II. Длина кривой заданной параметрически.
x=φ(t),t
[α,β] ;
y = ψ(t),
Функции ψ(t),φ(t),φ'(t) непрерывны на отрезке [α,β], причемφ'(t) ≠ 0.
Используем формулу:
L=
dx, ранее было установлено,
что
(для
параметрической функции), и пусть φ(α)
= а; φ(β) =b, найдемdx= φ'(t)dt, тогда
сделаем замену в интервале
L
=
dx =
φ'(t)dt =
dt
или
L=
dt.
Пример: найти длину одной арки циклоиды.
x = a (t –sin(t)),
y
= a (1 –cos(t)), t
[0,
2π];
x´t = a (1 –cos(t)); y´t = a sin(t);
=
= a
= a
=
=
a
= 2a sin
;
y
0 2πa x
L
=
2a
sin
dt = 4a
sin
d(
)
= –4a cos
=
–4a (-1-1) = 8a;
L
= 2
2a
sin
dt = 8a
sin
d(
)
= –8 a cos
= 8a;
III. Длина дуги в полярных координатах.
Пусть
кривая задана а полярной системе
координат p=ƒ(φ),φ
[α,β] , используем формулу:
x = p cos(φ) = ƒ(φ) cos(φ);
y = p sin(φ) = ƒ(φ) sin(φ);
последнюю запись можно рассмотреть как параметрическое задание функции, где параметром является φ.
L
=
dφ;
x'φ = ƒ'(φ)cos(φ) – ƒ(φ)sin(φ);
y'φ = ƒ'(φ)sin(φ) + ƒ(φ)cos(φ);
(x'φ)2= (ƒ'(φ)) 2 cos2 (φ) – 2ƒ'(φ)ƒ(φ)cos(φ)sin(φ) + (ƒ(φ)) 2 sin2 (φ);
(y'φ)2= (ƒ'(φ)) 2 sin2 (φ) + 2ƒ'(φ)ƒ(φ)cos(φ)sin(φ) + (ƒ(φ)) 2 cos2 (φ);
(x'φ)2+ (y'φ)2= (ƒ'(φ)) 2+ (ƒ(φ)) 2, тогда получаем
L=
dφ;
Пример: найти длину кривой p=a(1 –cos(φ));
φ
= 0; p = 0;
φ
=
p = a;кардиоида
φ
=π
; p = 2a;
a
φ
=
;
p=a;
2а 0
p
φ =2π ; p =0;
p' = a sin φ;
L
=2
dφ
= 2
d
=
=
2a
dφ =
2a
dφ = 2a
dφ =
=
-8a cos
= 8a (1-0) = 8a.
Вычисление объема тела по площади параллельных сечений.
Дано
тело, ограниченное замкнутой поверхностью.
В каждой точке x
[a,b].
Известна площадь сечения этого тела
плоскостью перпендикулярной оси Ох.
Эта площадь зависит
от х, является функцией от х.
a x1 xi-1 ζi xi b x
Обозначим эту функцию, Q(x) – непрерывна на отрезке [a,b].
Разобьем отрезок [a,b] наnчастей точками:a =x0<x1<..<xi-1<xi<..<xn =b;
Проведем через эти точки плоскости перпендикулярные оси Ох, которые разбивают тело на слои.
Выберем в каждой части отрезка [xi-1,xi] произвольные точки ζi (i=1,n) и найдем значение функции в этой точке, т.е.Q(ζi).
Каждый слой заменим цилиндром с основанием равным Q(ζi) и высотой Δxi.
Так поступим с каждым слоем, в результате получили некоторое «ступенчатое тело». Объем такого цилиндра равен Q(ζi) Δxi = Δvi.
Тогда объем «ступенчатого тела»:
ΔV= 
=
.
За объем данного тела принимается предел, к которому стремится объем «ступенчатого тела», когда число точек деления неограниченно увеличивается:
ΔV
= 
=
Q(x)
dx.
Объем тела вращения.
Дана криволинейная трапеция, ограниченная прямыми x=a,x=b, осью Ох и кривойy=ƒ(x). Эта трапеция вращается вокруг оси Ох. В результате получили тело.
Сечение этого теле в каждой
точке есть
yкруг
с
радиусом ƒ(x).
y=ƒ(x) Значит площадь ьакого сечения
Q(x) = πy2 = πƒ2 (x).
ƒ(x) Объем этого тела равен:
a x b
x
Vox
=
πy2dx
= π
y2dx.
Аналогично находится площадь фигуры с осью Оу.
Фигура ограничена линиямиcиd, осью Оу и
у x= ƒ(y).
Voy
= π
x2dy.
x
Пример: найти объем тела, полученного вращением эллипса вокруг оси Ox.
;
V
= 2
πy2dx
;
y
b
-a a x
-b
y2
= b2
(1 -
)
; V = 2π
b2 (1
–
)dx
= 2π b2
(x
–
)
= 2π b2(a
–
)
=
=
;
Применение определенного интеграла для решения некоторых физических задач.
1) Определить давление воды на вертикальную пластину, имеющую форму трапеции, размеры которой указаны на чертеже.
Возьмем элементарный слой равный dx.
a B
x
y
dx E
y D a-y
h
b A a-b C
x
Заштрихованную площадку примем за прямоугольник, тогда ее S=y·dx.
Давление на эту площадку будет зависеть от глубины ыводы и от удельного веса.
dp = δxy·dx. ΔDBE ∞ ΔABC.
;
ah
–hy = (a –b)x; y =
;
dp
= δx
dx;
P
=
dx
= δ
= δ
=
=
;
2) Вычислить работу, необходимую для выкачивания из цилиндрического резервуара высотой h=6и радиусом основанияR=2, если его ось имеет горизонтальное направление.
Δ = 0.9;
h
x y
R R-x
x
y
R
Вырежем слой толщиной dx.
dA = dp · x;
dp = δyH·dx ; dA = δx·yH·dx;
A
=
δH·xydx;
;
y =2
;
A
= 2 δH
x
dx
= | R = x = Rsin(t); x = R(1-sin(t)); dx=-Rcos(t) dt;
= R cos(t); при x = 0; t =
;
при x = 2R; t= –
|
= –2δH
R(1
-sin(t)) ·
·R2·cos2(t)dt
=2δHR3
(
cos2(t)
– cos2(t)sin(t))dt
= 2δHR3
+
=
=
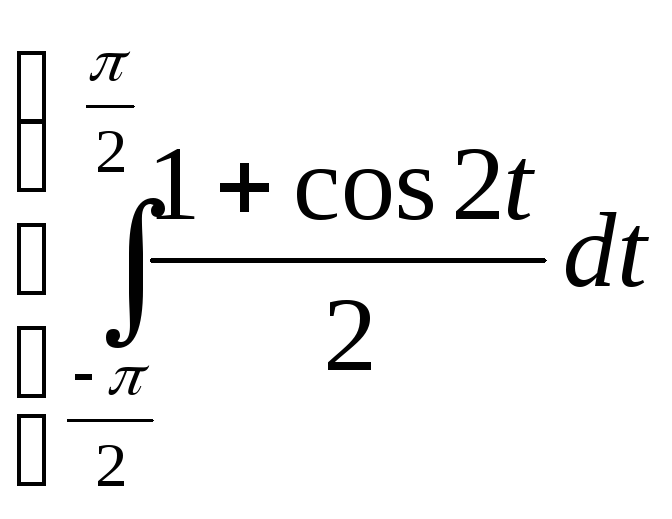δHR3
(t +
sin2t)
= π δHR3
= π·6·0.9·8;