Раздел III.

Приложение определенного интеграла.

§1. Площадь плоской фигуры.

Ранее было установлено, что площадь криволинейной трапеции есть :

S=, из свойства определенного интеграла видно, что ƒ(х) ≥ 0, то≥ 0,

т.е.S≥ 0; если ƒ(х) ≤ 0 , то≤ 0, тоS= ││;

y S = S1 + |S2 | + S3.

s1 s3

s2 x

Пример: найти площадь фигуры, ограниченной осью Ох и кривой y=cos(x) , гдеx.

1

S1 π

0 x

S2

S1 = = 1; S2 = = –1 ;

S = S1 + | S2| = 1 + 1 = 2.

Площадь криволинейной трапеции, если функция задана параметрически.

Пусть кривая задана параметрически, уравнениями:

х = φ(t) ,t

y = ψ (t),

где φ(t), φ'(t) и ψ (t) непрерывны на отрезке [α,β].

S=== |сделаем замену переменной| = |x= φ(t),dx= φ'(t)dt; |;

S = = | φ(α) =a; φ(β) =b; | = .

S = =.

Пример: Найти площадь фигуры, ограниченной осью Ох и одной аркой циклоиды.

x = a( t-sin(t) ); y

y = a ( 1- cos(t));

при t= 0;x=0;y=0;

t = π; x=aπ; y=2a;

t = 2π; x=2πa; y=0;

φ'(t) = a – acos(t) = a (1-cos(t));

0 aπ 2aπ x

S = = = a²= a²=

= a²= a²= 3πa².

Пример2: Найти площадь фигуры, ограниченной кривой заданной параметрически:

x = a sin³(t); y

y = a cos³(t);

при t = 0; x=0; y=a; a

t = π/2; x=a; y=0;

t = π; x=0; y= -a; -a a

t=3π/2; x=-a; y=0; 0 x

t = 2π; x=0; y=a;

достаточно рассмотреть одну четверть: - a

S = 4;

Площадь криволинейного сектора.

Рассмотрим полярную систему координат. В ней задана функция p=ƒ(φ), где ƒ(φ) непрерывна на отрезке [α,β].

p = ƒ(φ)

Δφi

β

α

0. P

Разобьем эту фигуру лучами:

α = φ0 <φ1 <.. < φi-1 < φi<..< φn = β

Δφi = φi – φi-1, i = ;

В каждом частичном отрезке [φi-1, φi ] выберем произвольное значение функции в этих точках, то есть. Каждый криволинейный сектор заменим круговым сектором с радиусом, так поступим с каждым в отдельности круговым сектором. Площадь одного кругового сектора:Si =.

Просуммируем эти секторы, получим:

Sn = = = ;

За площадь криволинейного сектора принимается предел, к которому стремится площадь «ступенчатой фигуры», когда число точек деления неограниченно увеличивается.

S= Sn = ,

Так как функция ƒ(φ) – непрерывна на отрезке [α,β], то этот предел есть определенный интеграл.

S= = ;

S= - площадь криволинейного сектора.

Пример: найти площадь фигуры, ограниченной кривой

p = a cos3φ; где а =const ; p≥0;

π/6

0 a p

1. p=a; cos3φ=1; 3 φ = 0 + 2πn; φ=;

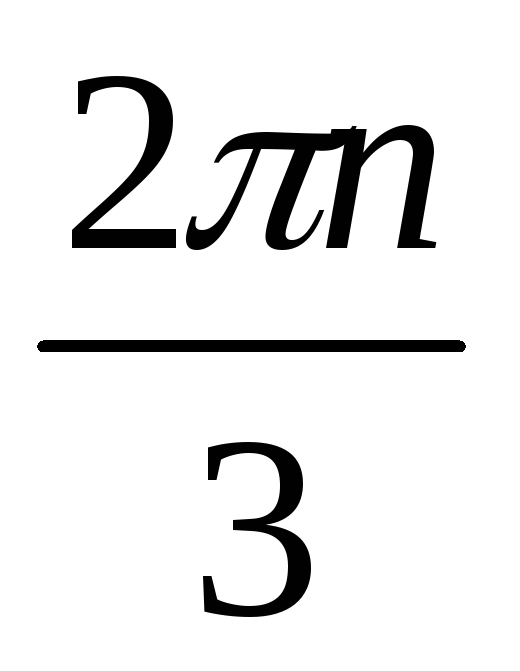при n=0;φ=0;

n=1; φ=;

n=2; φ=;

2. p = 0; cos3φ=0; φ=;

φ=; φ= –;

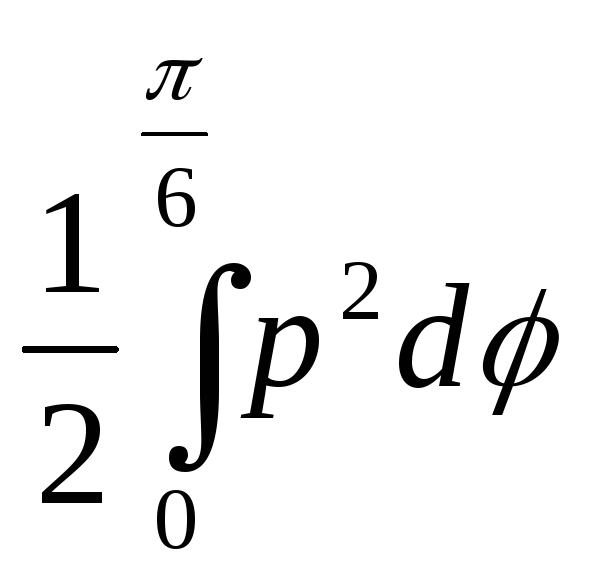S= 6·= 3= 3a²==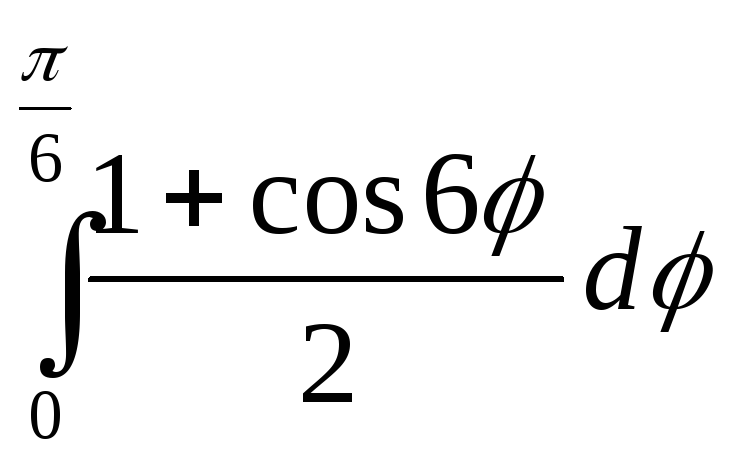

= =;

Длина дуги кривой.