Раздел I.

§1. Неопределенный интеграл и его свойства.

Определение 1.: ФункцияF(x) называется первообразной для функции ƒ(x) на некотором отрезке [a,b], если для всех из этого отрезка выполняется равенство:

F'(x)= ƒ(x).

Пример: F(x)=cos(x)+C; ƒ(x)=sin(x);

Теорема1. Если F1(x) иF2(x) какие-либо первообразные для функции ƒ(x) на отрезке [a,b], то выполняется соотношение:

F1(x) – F2(x) = C;

Доказательство.

Так как F1(x) первообразная для функции ƒ(x), тоF1'(x)= ƒ(x).

Так как F2(x) первообразная для функции ƒ(x), тоF2'(x)= ƒ(x).

Вычтем из первого равенства второе:

F1' (x) – F2'(x) = 0,

(F1(x) – F2(x))' = 0;

Обозначим F1(x) –F2(x)=φ(x), тогда φ'(x)=0;

Покажем, что φ(x) принимает постоянные значения.

Применим φ(x) на отрезке [a,x] теорему Лагранжа.

φ(x) – φ(a) = φ'(ξ)(x-a), a< ξ <x ,

так как φ'(ξ)=0, то φ(x) – φ(a) =0, то есть φ(x) = φ(a).

φ(a) = С, φ(x) =С;

F1(x) – F2(x) = C;

Замечание: из теоремы следует, что, еслиF(x) первообразная для ƒ(x), то (F(x)+С ) тоже первообразная.

Определение 2.: Совокупность первообразных, т.е. (F(x)+С), для ƒ(x) на [a,b] называется неопределенным интегралом отf(x) и обозначается:

∫ ƒ(x)dx=F(x) +C, причемF'(x) = ƒ(x),

ƒ(x) – называется подынтегральной функцией;

ƒ(x)dx– называется подынтегральным выражением;

Свойства неопределенного интеграла:

1. (∫ƒ(x)dx)' = ƒ(x);

Доказательство.

(∫ƒ(x)dx)' = (F(x)+C)' =F'(x) = ƒ(x);

2. d∫ƒ(x)dx= ƒ(x)dx;

Доказательство.

d ∫ƒ(x)dx= (∫ƒ(x)dx)' ·dx= | по свойству 1| = ƒ(x)dx;

3. ∫d F(x) = F(x) + C;

Доказательство.

Возьмем дифференциал от левой части:

d∫dF(x) =dF(x) (по свойству 2 )

найдем дифференциал от правой части:

d (F(x) + C) = dF(x) + dC = dF(x)

Получили, что обе части равны.

4. ∫(ƒ1(x)+ ƒ2(x))dx=∫ƒ1(x)dx+∫ƒ2(x)dx.

Найдем производную от левой и от правой частей:

(∫(ƒ1(x)+ ƒ2(x))dx)' = |по св-ву 1| = ƒ1(x)+ ƒ2(x)

(∫ƒ1(x)dx+∫ƒ2(x)dx)' = (∫ƒ1(x)dx+∫ƒ2(x)dx)' = ƒ1(x) + ƒ2(x).

5. ∫k·ƒ(x)dx=k·∫ƒ(x)dx, гдеk– постоянный множитель.

Доказательство.

(∫k·ƒ(x)dx)' =k·ƒ(x);

(k·∫ƒ(x)dx)' =k·(∫ƒ(x)dx)' =k·∫ƒ(x);

6. Формулы интегрирования не меняет свой вид при подстановке вместо независимой переменной xнекоторой функцииu(x), т.е. если∫ƒ(x)dx=F(x) +C;

∫ƒ(u)du = F(u) + C;

Доказательство.

Имеем: ∫ƒ(x)dx=F(x) +C;

F'(x) = ƒ(x),

Так как дифференциал первого порядка обладает свойством инвариантности, т.е. форма его не зависит от того является ли xнезависимой переменной или некоторой функцией

от x, то дифференциал

dF(u) = F'(u)du = ƒ(u)du

F'(u) = ƒ(u)

∫ƒ(u)du=∫dF(u) = | по свойству 3 | =F(u) +C.

Таблица основных интегралов.

1. ∫xαdx=xα+1/ (α+1) +C α ≠-1	1. ∫ uα du = uα+1/ (α+1) + C α ≠-1
2. = ln |x| + C	2. = ln |u| + C
3. ∫ ex= ex + C	3. ∫ eu = eu + C
4. ∫ ax dx = ax/lna + C	4. audu = au/lna + C
5. ∫ sin(x)dx = - cos(x) + C	5. ∫ sin(u)du= - cos(u) + C
6. ∫ cos(x)dx = sin(x) + C	6. ∫ cos(u)du = sin(u) + C
7. = tg(x) + C	7. = tg(u) + C
8. = -ctg(x) + C	8. = -ctg(u) + C
9.= arcsin ()+ C	9. = arcsin ()+C

10. =ln | x + | + C	10. =ln |u + | + C
11. =arctg()+C	11. =arctg()+C
12. =ln || + C	12. =ln || + C
13=ln || + C	13. =ln || + C
14. = ln |tg()| + C	14. = ln |tg()| + C
15. = ln |tg()| + C	15. = ln |tg()| + C
16.∫ tg(x) dx = – ln |cos(x)| + C	16.∫ tg(u) du = – ln |cos(u)| + C
17.∫ ctg(x) dx = ln |sin(x)| + C	17.∫ ctg(u) du = ln |sin(u)| + C

Проверим формулу 9.

(arcsin)' = = = ;

Проверим формулу 10.

(ln| x + | )' = ==;

Проверим формулу 11.

(arctg)' ==;

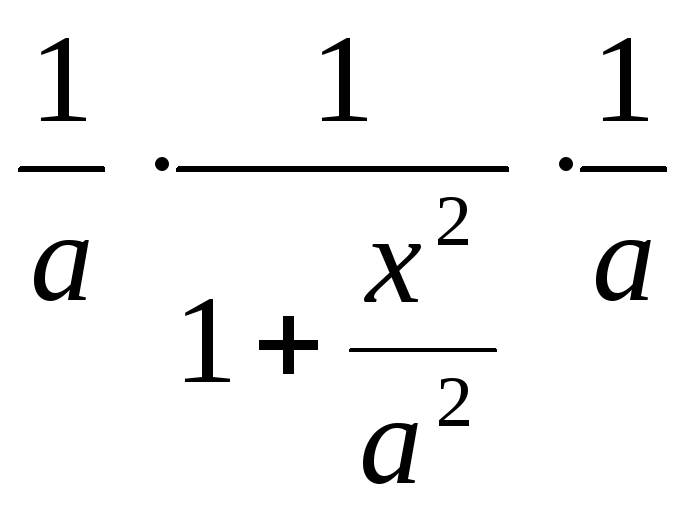Поверим формулу 12.

(a ∙ ln ||)' = = = ;

Проверим формулу 14.

(ln |tg()|)' = ==;

Проверим формулу 15.

Пусть cos(x) = sin(x + )

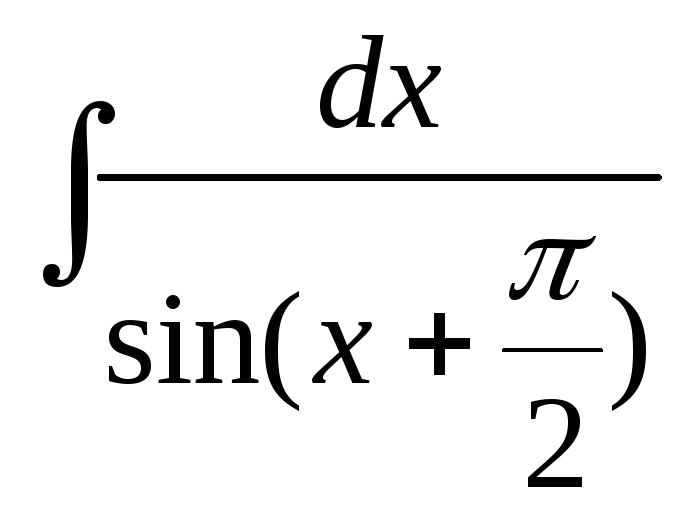= = ln |tg()| + C;

Проверим формулу 16.

∫ tg(x)dx=∫ = –∫– = -∫ = –∫ = –ln|cos(x)| +C;

Проверим формулу 17.

∫ ctg(x) dx = ∫ =∫ = = ln |sin(x)| + C;

Пример:

1. ∫dx=∫ (8-3x)^6/5dx= |d(8-3x) = – 3dx| = –∫ (8-3x)^6/5(– 3dx) =

–∫(8 –3x)^6/5 d(8-3x) = – (8-3x)^11/5 + C.

_____

2. ∫ x √4 + x² dx = ∫ (4 + x²)^1/2x dx = | d(4 + x²) = 2x dx| = 1/2 · ∫ (4 + x²)^1/22x dx =

=· ∫(4 + x²)^1/2 d(4 + x²) = =+ C;

______

3. ∫ ³√ sin²(x) · cos(x)dx = ∫ (sin(x))^2/3 d(sin(x)) = 5/3 (sin(x))^5/3 + C

4. Найти интеграл.

dx= dx = | | = =arcsin (x³) + C.