23.Цель и особенности эксперимента по определению функциональной зависимости.

Цель – установить функциональную зависимость распределения значений, полученных в ходе эксперимента.

Задача выбора вида мат. модели неформулируема. (не решаема математически, т.к. нельзя определить зависимость для всех случаев распределений). Главный критерий выбора – удобство.

Требования к математ. Модели:

1. Удобство (компактность математич. выражения )

Любую функцию можно описать многочленом:

2. Чтобы параметры (коэффициенты) отражали физические величины процесса интерпретации параметров полученной функциональной зависимости.

y=F(x₁, x₂, ….x_n)- многофакторная зависимость.

y=f(x) – однофакторная зависимость

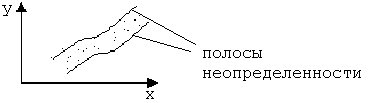
24.Выбор вида математической модели.

выбора вида мат. модели неформулируема. (не решаема математически, т.к. нельзя определить зависимость для всех случаев распределений). Главный критерий выбора – удобство.

Требования к математ. Модели:

1. Удобство (компактность математич. выражения )

Любую функцию можно описать многочленом:

2. Чтобы параметры (коэффициенты) отражали физические величины процесса интерпретации параметров полученной функциональной зависимости.

y=F(x₁, x₂, ….x_n)- многофакторная зависимость.

y=f(x) – однофакторная зависимость

25.Быстрые методы установления графического вида однофакторных зависимостей.

Получили зависимость:

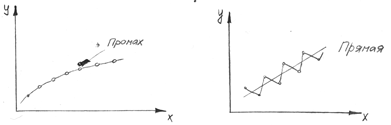
1. Метод обведения контура:

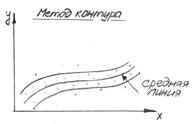
Средняя линия – графические функциональные зависимости.

Нужно удалять промахи!!!

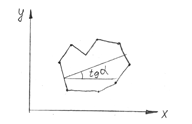
2. Метод медианных центров:

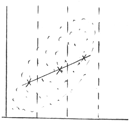
Делят на несколько участков и применяют метод медиан (от Х одинаковое число точек снизу и сверху, справа и слева).

3. Метод выделения остатков:

У=f(x)

f(x)=f₁(x)+f₂(x)

f₁(x) =y₀

y= f₂(x) + y₀

f₂(x) = f₃(x) + f₄(x)

f₃(x) =ax²

y= y₀+ax²+f₄(x)

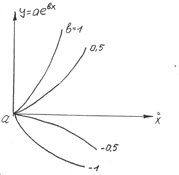
y=axⁿ

lny =lna +nlnx

y=b+b₁x

26. Подбор аппроксимирующих функций.

Целью совместных измерений является установление функциональной зависимости между величинами. Для отыскания зависимости y=f(x) между переменными x и y необходимо последовательно устанавливая и измеряя значения x, одновременно измерять величину у, получив таким образом координаты исследуемой зависимости (х_i, y_i). Исключив возможные систематические погрешности, можно уточнить координаты, но и уточненные координаты могут отклоняться от истинной зависимости из-за наличия случайных погрешностей. Поэтому при выполнении совместных измерений, во-первых, возникает задача аппроксимизации зависимости y=f(x) по экспериментальным данным так, чтобы она наилучшим образом описывала истинную зависимость.

Аппроксимирующая функция – алгебраическое уравнение функции с коэффициентами.

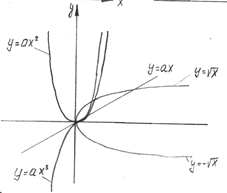
У нас есть экспериментальные данные. Используя их, строим график. По виду этого графика определяем с какой зависимостью (линейной, гиперболической, показательной, степенной, логарифмической) мы имеем дело.

Если у нас нелинейная зависимость, то мы должны осуществить линеаризацию, т.е. построить график в таких осях, чтобы получить прямую линию.

y=ахⁿ ; lny=lna+nlnx (lny заменяем на y, lna на b, nlnx на b₁x), получим у= b+ b₁x

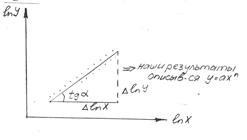
tgα=n=∆lny/∆lnx

Но если результаты не легли на прямую, значит подбираем другую функцию.

Логарифмирование:

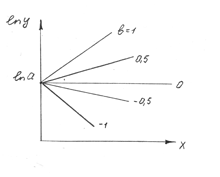
lny=lna+bx

Дробно-рациональная функция (не всегда легко узнаваемая).

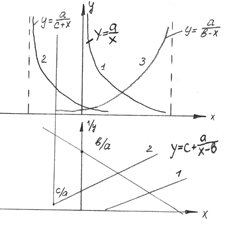
Виды функциональной зависимости: