Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

Пусть функция   имеет   производную в некоторой окрестности точки  ,  Пусть  Пусть   — произвольное положительное число, тогда:   точка   при   или   при  :

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

Запишем остаточный член в общей форме:

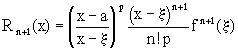 , где a< <x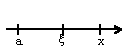 

(x< <a   ). Отметим, что   зависит от x, n, p.

Очевидно, найдется такое число   (  зависит от x, n, p): 0< <1, что

-a= (x-a). Отсюда  =a+ (x-a), x- =(x-a) -  (x-a)=(x-a)(1- ) и  .

Итак,  .

1. Пусть p=n+1, тогда   - остаточный член в форме Лагранжа.

2. Если p=1, то    - остаточный член в форме Коши.

Отметим, что в этих формулах значения  , вообще говоря, считаются различными, так как   зависит от р, которое различно в этих формулах.

Сформулируем без доказательства следующую теорему.

Теорема. Пусть функция f(x) имеет производные до порядка (n-1) в некоторой окрестности точки а и производную порядка n в самой точке а, тогда справедливо равенство   (бесконечно малая при х  а более высокого порядка малости, чем  ). Последняя формула есть остаточный член в форме Пеано.

7. Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида   и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

8. Откры́тое мно́жество — это множество, каждый элемент которого входит в него вместе с некоторой окрестностью. Открытое множество является фундаментальным понятием общей топологии. За́мкнутые мно́жества в общей топологии, функциональном анализе и математическом анализе — это дополнения к открытым множествам. Замкнутое множество содержит все своиточки прикосновения.

36. Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М С помощью кванторов определение запишется следующим образом: М ∈ Ε – открытое, если    ∀ у∈М   ∃ ε>0 :  U_ε(y) < M

Простым языком – открытое множество состоит из внутренних точек. Примерами открытого множества являются пустое множество, прямая, интервал (а, b)

Множество называется замкнутым, если ему принадлежат все граничные точки. Пример – отрезок [a, b]

Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).

Докажем несколько теорем, связанных с открытым и замкнутым множествами.

7. Для функции нескольких переменных   можно определить понятие предела по одной из переменных   при фиксированных значениях остальных переменных. В связи с этим возникает понятие повторного предела.

8. Будем говорить, что последовательность точек   сходится при   к точке  , если   при  .

         В этом случае точку   называют пределом указанной последовательности и пишут:   при .

         Легко показать, что   тогда и только тогда, когда одновременно  ,   (т.е. сходимость последовательности точек пространства   эквивалентна покоординатной сходимости).

7. Д. п. последовательности, предел двойной последовательности {х _тп}, т, n=1, 2, ...,- число а, определяемое следующим образом: для любого е>0 существует такое N_e, что для всех m>N_e и n>N_e выполняется неравенство

Обозначение: 

Если для любого e>0 существует такое N_e, что для всех m>N_e и n>N_e выполняется неравенство |x_mn|>e, то последовательность х _тп имеет своим пределом бесконечность:

Рассмотрим функцию двух переменных  , определенную в некоторой выколотой окрестности точки  . Выберем и зафиксируем переменную  . Получим функцию как бы одной переменной. Рассмотрим предел:

Будем считать, что   существует. Теперь снимем фиксацию с переменной   и рассмотрим следующий предел:

Если этот предел существует, то говорят, что   есть повторный предел функции   в точке  .

Аналогично мы можем фиксировать сначала переменную  . В этом случае мы также получим повторный предел, но, вообще говоря, другой:

Это определение можно распространить и на функции нескольких переменных  .