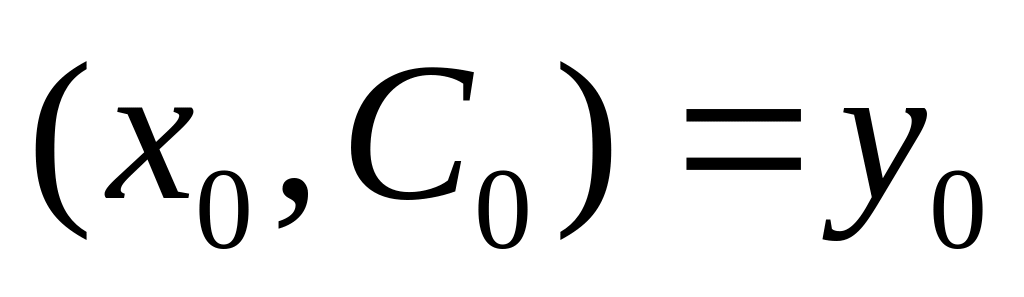14. Вычисление 2го инт.

П-уг ОБЛ. Пусть обл-ть D задана нер-вами т.е. изобр-ся п-угком. Тогда двойной интеграл вычисляется по одной из формул 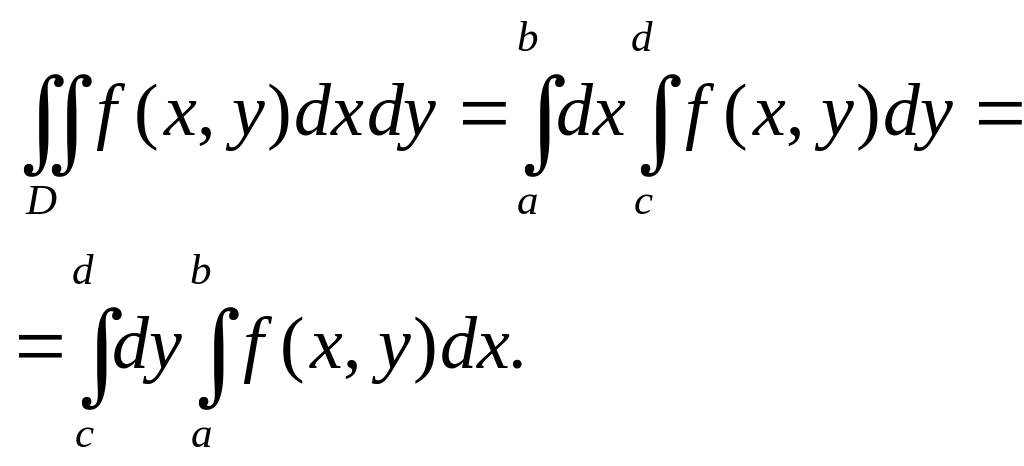В 1-й формуле сначала вычисляется внутренний интеграл . В процессе этого интегрирования x рассм-ся как постоянная величина. Но результат интегрирования рассм-ся как ф-ция от х, и второе интегрирование (в пределах от a до b) выполняется по аргументу x. Во 2-й формуле порядок действий обратный.

СЛУЧАЙ ПРОИЗВОЛЬНОЙ ОБЛАСТИ. обл-ть D задаётся неравенствами . [a, b – крайние абсциссы обл-ти, φ₁(x), φ₂(x) – ф-ции, выражающие ординаты нижней и верхней граничных линий].

18. ВЫЧИСЛ 3Х ИНТ. Пусть обла-ю инт-ния является тело, огранич снизу пове-тью z=z₁(x,y), сверху – поверхностью z=z₂(x,y), причем f(x,y) и g(x,y) – непрерывные ф-ции в замкнутой области D, являющейся проекцией тела на плоскость Oxy. Будем считать область V – правильной в напр оси Oz: любая прямая параллельная оси Oz, пересекает границу области не более чем в двух точках. Тогда для любой непрерывной в области V ф-ции f(x,y,z) имеет место формула 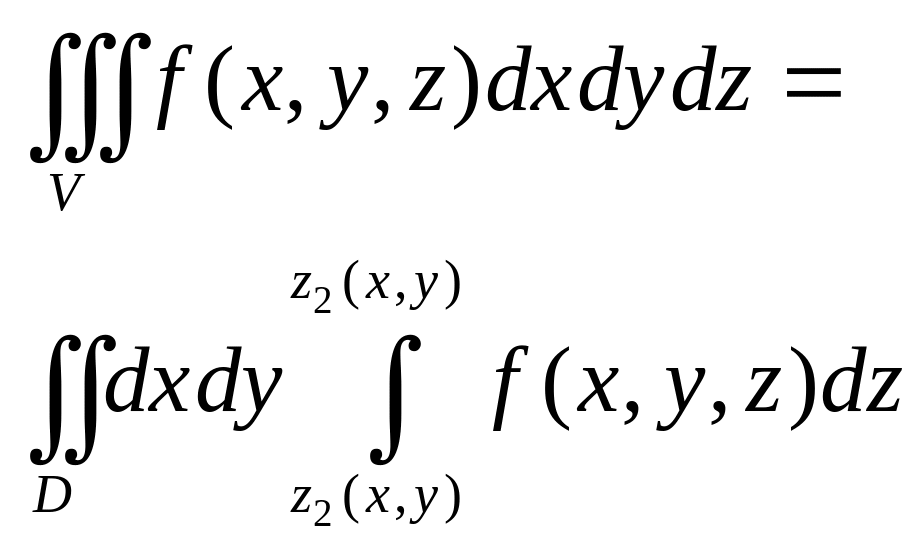. В процессе вычисления интеграла величины x, y являются постоянными. Результат вычисления рассматривается как ф-ция аргументов x,y. После того как интегрирование по переменной z выполнено, правая часть превращается в двойной интеграл. Поэтому в итоге тройной интеграл сводится к повторному:

23. Лду 1 пор, ур бернулли

Линейным уравнением 1-го порядка называют

уравнения вида:

1. y’+yP(x)=Q(x) – где P(x) и Q(x) некоторые

функции переменной х , а y’ и y входят в уравнение

в 1 степени.

24. Оду первого порядка в полных дифференциалах

Определение 15. ОДУ первого порядка

, (6)

где функции - непрерывны в области а левая часть -полный диф-ал некот диф-мой функции назовем ОДУ в полных дифференциалах.

20. Дифф ур. Осн понятия.

Общий вид диф уравнения F(x, y, y’)=0 y’=f(x,y) (1).

Решением дифференциальное уравнение первого порядка наз-тся всякая функция y=(x), которая будучи подставлена в данное уравнение обращает его в тожд.

’(x)= f (x, (x)); Задача Коши для диф. ур 1пор.

Требуется найти решение диф. ур-я (1) удовлетворяющего следующему условию (2). Теорема Коши. Пусть задана на плоскости XOY некоторая обл. Д и задано диф. ур-е разрешённое относительно производной, тогда если функция f(x, y) и её частная производная непрерывны в обл. Д, и некоторая фиксированная точка обл. Д, то существует и единственная функция y=(x) являющаяся решением (1) и такая, которая в т. принимает значение , т.е. уд-щая зад нач условию . Т.е. если существует решение диф. ур-я, то таких решений беск мн-во. График функции явл-ся решением диф. ур-я принято называть инт кривой, процесс реш-я – инт-нием. Точку в плоскости XOY называют особой точкой диф. ур-я если в этой т. не выполняется условие теоремы Коши, т.е. особая т. это такая т. через которую может вообще не проходить ни одной интегральной кривой, либо проходить множество. Решения диф. ур-я в каждой т. которого нарушается условие единственности из теоремы Коши, принято называть особым решением диф. ур-я. График особого решения называется особой кривой. Определение общего решения диф. ур-я 1 порядка:б Функция y=(x, C), где С произвольная константа, называется общим решением диф. ур-я (1) если выполнены следующие условия:

1. Функция y=(x, C) является решением ур-я (1) при любом значении произвольной константы С;

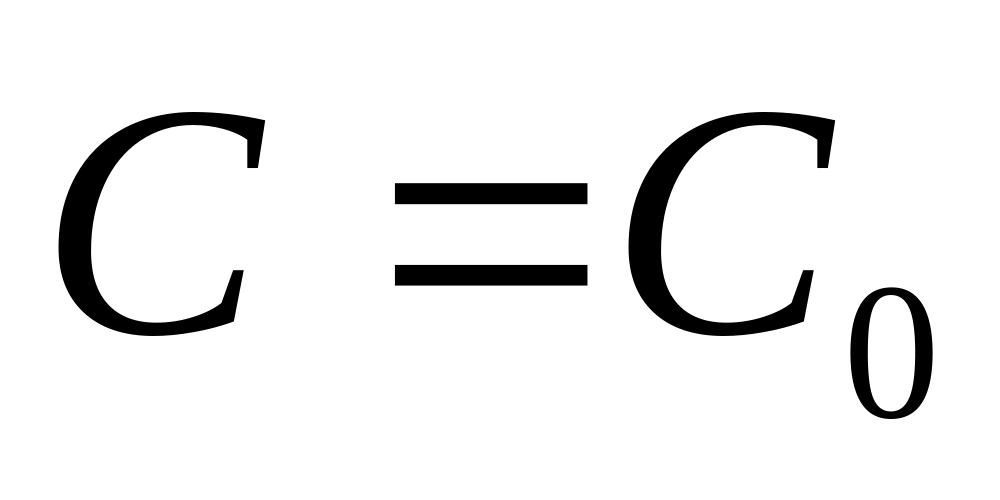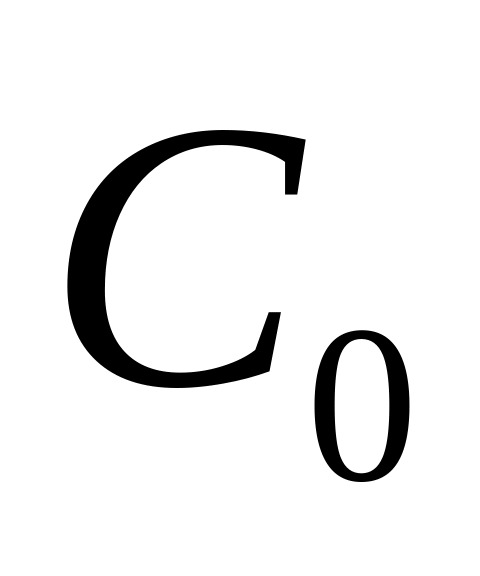2. Какова бы ни была т.  Д найдётся такое значение произвольной константы , что функция y=(x, ) удовлетворяет заданному начальному условию, т.е. 