8. Частные производные.

Опр. Пусть в некот обл задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение х к переменной х. Тогда величина _xz = f( x + x, y) – f(x, y) называется частным приращением функции по х.

. Тогда - частн производной функции z = f(x, y) по х.

Обозн: Аналогично определяется частная производная функции по у.

Геометрич смыслом частной производной (допустим ) - тангенс угла наклона касат, проведенной в точке N₀(x₀, y₀, z₀) к сечению поверхности плоскостью у = у₀.

Полное приращение и полный дифференциал. Опред. Для функции f(x, y) выражение z = f( x + x, y + y) – f(x, y) - полным приращением. Если функция f(x, y) имеет непрерывные частные производные, то

Применим теорему Лагранжа к выр в квадратных скобках.

здес

Тогда получаем

Т.к. частные производные непрерывны, то можно записать равенства:

Опред. Выражение назыв полным приращ функции f(x, y) в некоторой точке (х, у), где ₁ и ₂ – бесконечно малые функции при х  0 и у  0 соответственно. Опред: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно х и у приращения функции z в точке (х, у).

Для функции произвольного числа переменных:

10. Частные производные высших порядков. Если ф-я f(x, y) определена в некот обл D, то ее частные производные и тоже будут определены в той же области или ее части. Б называть эти производные частными производными первого порядка. Производные этих функций будут частными производными второго порядка.

Продолжая дифф-вать получ рав-ва, получим частные производные более высоких порядков.

Опр. Частные производные вида и т.д. называются смеш производными.

Теорема. Если функция f(x, y) и ее частные производные определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение: .Т.е. частные произв высших порядков не зависят от порядка дифф-ния. Аналогично определяются дифференциалы высших порядков.

n – символич степень производной, на кот заменяется реальная степень после возведения в нее стоящего с скобках выр-я.

17. СВ-ВА 3ГО ИНТ. Тройной интеграл обл теми же свойствами, что и двойной интеграл: 1. , где C – константа. 2. 3 4. Теорема (о среднем). Если ф-ция z=f(x,y,z) непрерывна в области V, то в этой области найдётся такая точка где V – объем области V. ГЕОМ СМЫСЛ 3ГО ИНТ. Пусть ф-ция z=f(x,y,z) непрерывна и неотрицательна в пространственной обл-ти V. Тогда тройной интеграл численно равен объему области V, т.е. объёму тела: .

12. Экстремум функции нескольких переменных.

Необходимое и достаточное условие экстремума. Опр. Если для функции z = f(x, y), опр-ой в некот обл, в некот окрестности точки М₀(х₀, у₀) верно нер-во

то т М₀ называется т максимума.

Опр. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство то точка М₀ - точкой мин. Теор. (Необхо усл экстр). Если функция f(x,y) в точке (х₀, у₀) им экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует. Эту точку (х₀, у₀) будем называть критич т.

Теор. (Достат усл экстремума). Пусть в окрестности критической т (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

1. Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

- максимум, если - минимум.

2. Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

13. ПОНЯТИЕ ДВОЙНОГО ИНТЕГРАЛА. Пусть D – неко замкн огранич обл-ть. Построим покрывающую эту область решётку, заштрихуем ту часть, которая не покрыта полными клетками. Очевидно, что площадь этой части уменьшается по мере того, как увеличивается число клеток разбиения. Пронумеруем клетки решётки индексами i и j: . Δx_i – длина горизонтальной стороны клеток, Δy_i – длина вертикальной стороны при Δx_i→0, Δy_i→0. Площадь заштрихованной части тоже стремится к 0: S→0. Т.е., можно утверждать, что D_кл..→D. В каждой клетке выберем произвольную точку (ξ_i, η_i) и составим сумму , которую назовём интегральной суммой для ф-ции z=f(x,y) в обл-ти D. Назовём максимальным диаметром d обл-ти D наибольшее расстояние между граничными точками этой области: . Ф-ция z=f(x,y) наз-ся интегрируемой на множестве, если сущ-ет конечный предел интегрируемой суммы этой ф-ции. Само значение предела называется двойным интегралом от ф-ции z=f(x,y) по обл-ти D и обозначается

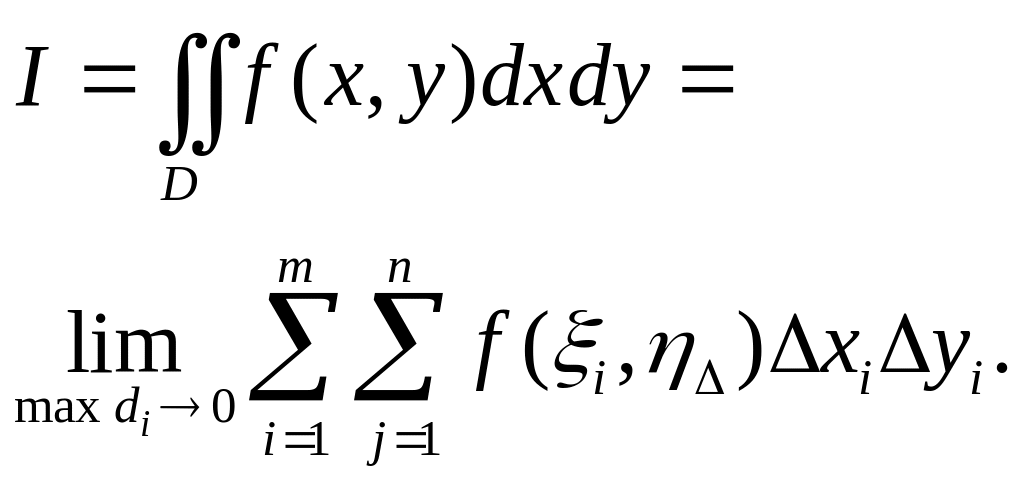
СВО-ВА 2 ИНТ-ЛА. 1. если C – произвольное число, и ф-ция f(x,y) интегрируема в обл-ти D, то ф-ция Cf(x,y) тоже интегрируема в D и , т.е. постоянный множитель можно выносить за знак интеграла. 2. Если ф-ции f(x,y) и g(x,y) интегрируемы в обл-ти D, то их алгебраическая сумма также интегрируема в этой области и 3. Если область D явл-ся объединением областей D1 и D2, не имеющих общих внутренних точек, в каждой из которых ф-ция z=f(x,y) интегрируема, то в обл-ти D эта ф-ция также интегрируема и 4. Теорема (о среднем). Если ф-ция z=f(x,y) непрерывна в обл-ти D, то в этой области найдётся такая точка где S – площадь фигуры D.