18 Вопрос. Второе начало термодинамики.

Первое начало термодинамики, выражая закон сохранения и превращение энергии. Не позволяет при этом установить направление протекания термодинамических процессах. Второе начало термодинамики дает ответ на вопрос какие процессы возможны в природе а какие нет. Используя понятия энтропии и неравенство Клаузиуса 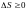второе начало термодинамики можно сформулировать как закон возрастания энтропии: любой необратимый процесс в замкнутой системе происходит так что энтропия при этом возрастает или другими словами в процессах проходящих в замкнутых системах энтропия не убывает. Формула Больцмана позволяет объяснит второе начало термодинамики возрастание энтропии означает переход системы из менее вероятных в более вероятные. 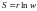Термодинамическая вероятность состояния системы это число способов которые могут быть реализовано данное состояние . Реальные процессы необратимы поэтому можно утверждать что все процессы замкнутой системы ведут к увеличению энтропии. Существуют еще 2 формулировки второго начало термодинамики. Формулировка по Кельвину невозможен круговой процесс, единственным результатом которого является превращение теплоты полученный от нагревателя в эквивалентную ей работу. По Клаузиуса невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому. Первые два начала дают недостаточно сведений о поведении термодинамических систем при абсолютном 0 поэтому они дополняются третьим началом термодинамики или теоремой Нернста Планка энтропия всех тел в состоянии равновесия стремится к 0 по мере приближения температуры к нулю Кельвина .

19 Вопрос. Цикл Карно.

Основываясь на второе начало термодинамики Карно вывел следующие теорему из все периодических действующих тепловых машин имеющих одинаковую температуры нагревателей Т1 и холодильников Т2 наибольшим КПД обладают обратимые машины при этом КПД машин работающих при одинаковых температурах Т1 и Т2 равны друг другу и не зависят от природы рабочего тела а определяются только температурами. Карно проанализировал цикл состоящий из двух изотерм и двух адиабат.

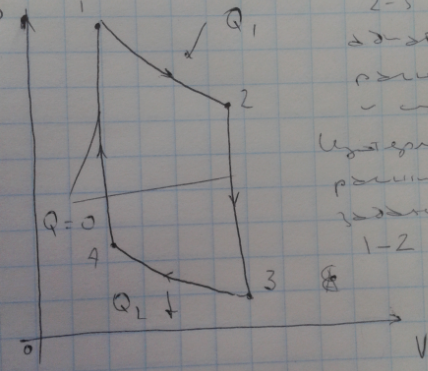
Изотермическое расширение и сжатие 1-2, 3-4. А адиабатное расширение 2-3, 4-1. При изотермическом расширении U=const и количество теплоты получаемым газом Q1= работе расширения. 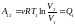. При адиабатном расширении отсутствует тепло обмен а работа расширения совершается за счет изменения внутренней энергии 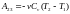. Количество теплоты отданная газом при изотермическом сжатии равно работе сжатия 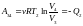. Работа адиабатного сжатия 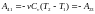. Работа совершаемая в результате кругового процесса 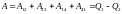. КПД цикла 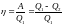. Применив уравнение Пуассона КПД цикла Карно . 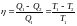То есть определяется температурами нагревателя и холодильника.

Вопрос 20. Силы и потенциальная энергия межмолекулярного взаимодействия.

Модель идеального газа, исп. в МКТ позволяет описывать поведение разряженных газов при достаточно высоких t^оC и низких Р.

При рассмотрении реальных газов, т.е. газов, св-ва которых зависят от взаимод. молекул необходимо учитывать силы межмолекул. взаимод-я. они проявл. на расстояниях r меньше 10^-9м и быстро убывают при увелич. расстояния между молекулами. Такие силы назыв. коротко действующими. По мере развития представлений о строении атома и квант механики было выяснено, что между молекулами в-ва одновременно действуют силы притяжения F_п и силы отталкивания F_от.

На расстоянии r=r_o результирующая сила F=0, т.е. F_п и F_от уравновешивают друг друга, т.е. r_o – расстояние, на котором находились бы молекулы при отсутствии теплового движения. При r больше r_o преобладает сила притяжения, на расстояниях r меньше r_o – силы отталкивания.

Элементарная работа силы F при увеличении расст. совершается за счёт уменьшения взаимной потенц. энергии молекул. Если молекулы находятся на расстоянии, на котором силы не действуют (R стремится к бесконечности).

При сближении молекул появляются силы притяжения, которые совершают положительную работу. Потенц. энергия уменьшается, достигая минимума, с уменьшением r силы отталкивания резко возрастают и совершаемая работа становится отрицательной. Критерием различных агрегатных состояний явл. соотношение между потенц. энергией и kT. Если E_п>kT, то в-во находится в тв. сост., т.к. молекулы не могут отдалиться на значит. расстояние и равновесие.

Если E_п много меньше kT, то в-во находится в газообразном состоянии, т.к. интенсивное тепловое движение молекул препятствует соед. молекул.

Если E_п примерно равна kT, то в-во находится в жидком сост., т.к. в результате теплового движ. молекулы перемещаясь в простр., обмениваясь местами, но не расходясь на расстояния, превышающее r_o.