4 Вопрос. Изо-процессы с точки зрения уравнение Клапейрона-Менделеева.

- Изотермический процесс .

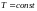Запишем уравнение Клапейрона-Менделеева

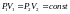
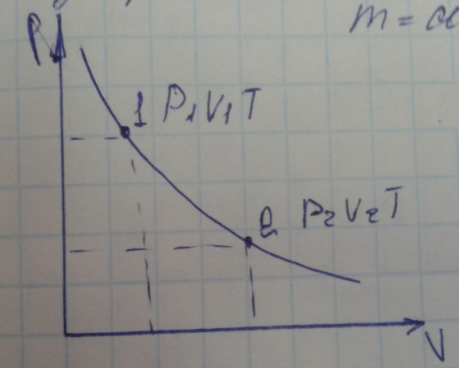- Изобарный процесс .

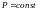1 .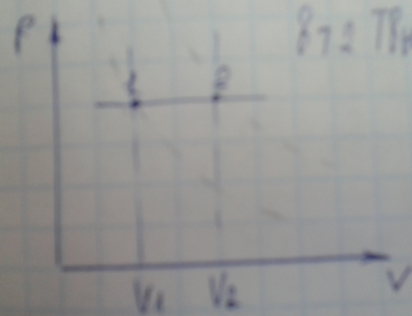

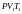
2.

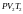
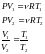
- Изохорный процесс.

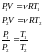
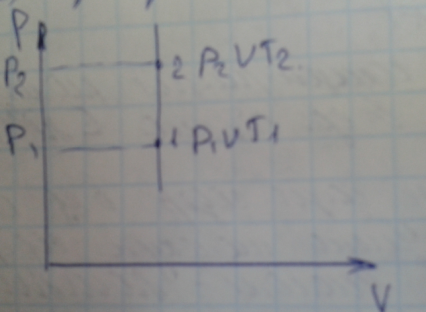
5 Вопрос. Закон Максвелла о распределения молекул газа по скоростям и энергиям теплового движения.

В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению из-за хаотического движения молекул все направления движения являются равно-вероятными, то есть в любом направлении в среднем движется одинаковое число молекул. По МКТ как бы не изменялись скорости молекул при столкновениях средняя квадратичная скорость молекулы массы 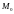при равновесном состоянии Т-const остается постоянной и равной

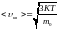
это объясняется тем что в газе находящимся в состоянии равновесия устанавливается некоторое стационарное состояние неменяющееся со временем распределения молекул газа по скоростям этот закон распределения теоретически был выведен Максвеллом.

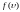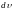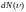Закон Максвелла описывается некоторой функцией распределения молекул газа по скоростям если разбить диапазон скоростей на малые интервалы то на каждый интервал скорости приходится некоторое число молекул от общего числа N. Функция определяет относительное число молекул 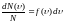скорости, которых лежат в интервале от до .

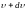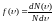
Принимая методы теории вероятности, Максвелл нашёл функцию .

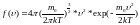Конкретный вид функции зависит от рода газа (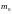 , 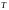и от параметров состояния)

График функции.

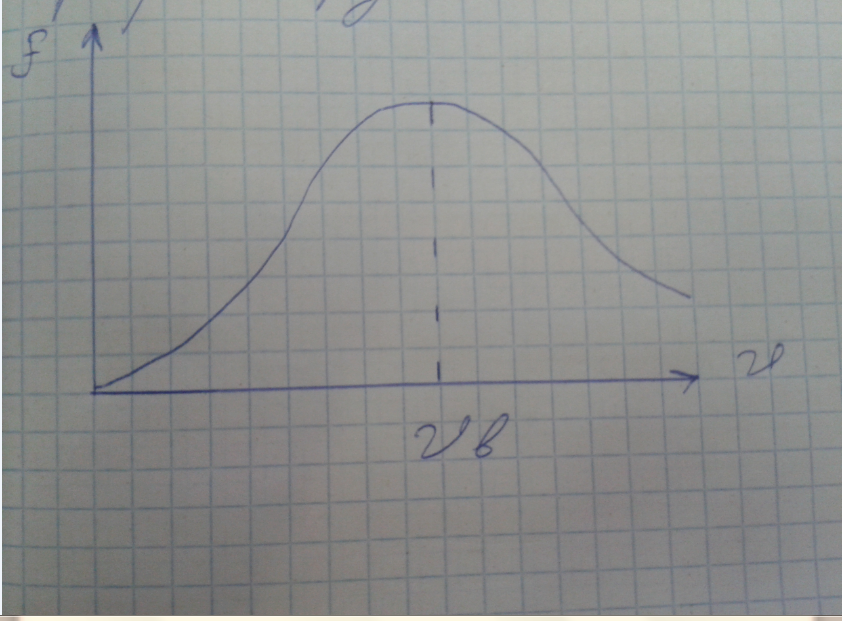
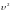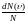Так как при возрастании множитель экспонента уменьшается быстрее, чем растет , относительное число молекул , скорости которых лежат в интервале _, находится как площадь заштрихованной полоски.

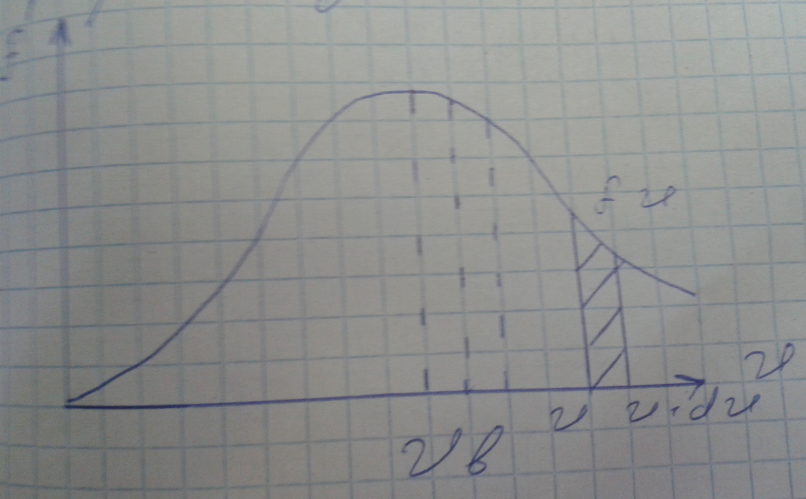
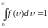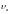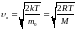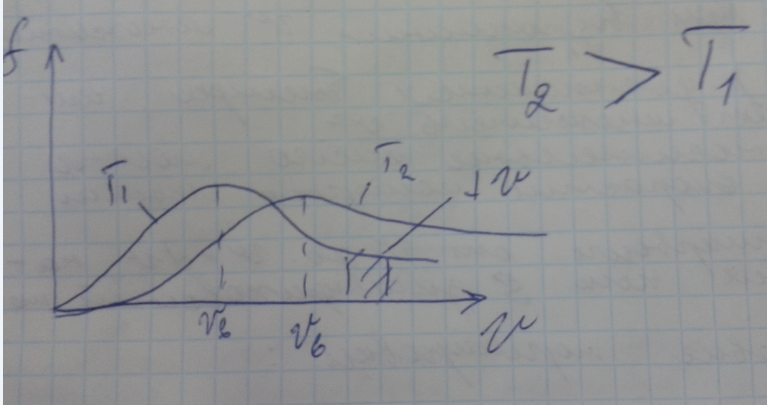
Функция удовлетворяет условию нормировки - это площадь ограниченная прямой и осью абсцисс. Максимум функции соответствует наиболее вероятной скорости . Значение можно найти продифференцировав уравнение . При повышении температуры максимум функции распределения сместится вправо и понизится - при этом значение становится больше, однако площадь ограниченная кривой остается неизменной поэтому при повышении температуры кривая растягивается и понижается.

Средняя скорость молекулы. 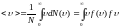подставляя сюда функцию и интегрируя, получим 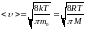. Исходя из распределения молекул по скоростям можно найти распределение молекул по значениям кинетической энергии. Перейдем от переменой к переменой 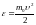. Подставив в функцию значение скорости 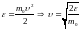и интервала скорости 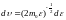получим функцию распределения молекул по энергиям теплового движения

.

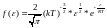Средняя кинетическая энергия идеального газа - .

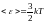6 Вопрос. Барометрическая формула. Распределение Больцмана.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру   и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения   одинаково), барометрическая формула имеет следующий вид:

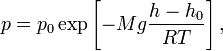
где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне

( ),   — молярная масса газа,   — газовая постоянная,   — абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону:

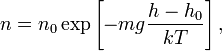
где   — масса молекулы газа,   — постоянная Больцмана.

Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле. При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе.

Распределение Больцмана — это распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия. Распределение Больцмана было открыто в 1868 - 1871 гг. австралийским  физиком Л. Больцманом. Согласно распределению, число частиц n_i с полной энергией E_i    равно:

n_i =A•ω_i •e^­E_i ^/Kt  (1)

где ω_i  - статистический вес (число возможных состояний частицы с энергией e_i). Постоянная А находится из условия, что сумма n_i по всем возможным значениям i равна заданному полному числу ч астиц N в системе (условие нормировки):

В случае, когда движение частиц подчиняется классической механике, энергию E_i можно считать состоящей из кинетической энергии E_iкин частицы (молекулы или атома), её внутренней  энергии E_iвн (напр., энергии возбуждения электронов) и потенциальной энергии E_i,_пот во внешнем поле, зависящей от положения частицы в пространстве:

E_i = E_i, кин + E _i, вн + E_i, пот            (2)

Распределение частиц по скоростям  является частным случаем распределения Больцмана. Оно имеет место, когда можно пренебречь внутренней энергией возбуждения

E_i,вн и влиянием внешних полей E_i,пот. В соответствии с (2) формулу (1) можно представить в виде произведения трёх экспонент, каждая из которых даёт распределение частиц по одному виду энергии.

В постоянном поле тяжести, создающем ускорение g, для частиц атмосферных газов вблизи поверхности Земли (или др. планет) потенциальная энергия пропорциональна их массе m и высоте H над поверхностью, т.е. E_{i, пот} = mgH. После подстановки этого значения в распределение Больцмана и суммирования по всевозможным значениям кинетической и внутренней энергий частиц получается барометрическая формула, выражающая закон уменьшения плотности атмосферы с высотой.

В астрофизике, особенно в теории звёздных спектров, распределение Больцмана часто используется для определения относительной заселённости электронами различныхуровней энергии атомов. Если обозначить индексами 1 и 2 два энергетических состояния атома, то из распределения следует:

n₂/n₁ = (ω₂/ω₁)•e^-(E₂^-E₁^)/kT            (3)      (ф-ла Больцмана).

 Разность энергий E₂-E₁ для двух нижних уровней энергии атома водорода >10 эВ, а значение kT, характеризующее энергию теплового движения частиц для атмосфер звёзд типа Солнца, составляет всего лишь 0,3-1 эВ. Поэтому водород в таких звёздных атмосферах находится в невозбуждённом состоянии. Так, в атмосферах звёзд, имеющих эффективную температуру Тэ > 5700 К (Солнце и др. звёзды), отношение чисел атомов водорода во втором и основном состояниях равно  4,2•10^-9.

Распределение Больцмана было получено в рамках классической статистики. В 1924-26 гг. была создана квантовая статистика. Она привела к открытию распределений Бозе - Эйнштейна (для частиц с целым спином) и Ферми - Дирака (для частиц с полуцелым спином). Оба эти распределения переходят в распределение, когда среднее число доступных для системы квантовых состояний значительно превышает число частиц в системе, т. о. когда на одну частицу приходится много квантовых состояний или, др. словами, когда степень заполнения квантовых состояний мала. Условие применимости распределении Больцмана можно записать в виде неравенства:

г де N - число частиц, V - объём системы.  Это неравенство  выполняется при высокой темп-ре и малом числе частиц в ед. объёма (N/V). Из этого следует, что чем больше масса частиц, тем для более широкого интервала изменений Т и N/V справедливо распределение Больцмана.